Численное интегрирование
При вычислении
определенных интегралов от функций,
заданных в виде таблицы или в явном виде
(
),
одним из численных методов используют
функции intsplin,
inttrap,
integrate,
intg.
Способ 1.
С помощью команды intsplin. Это интегрирование экспериментальных данных с помощью сплайн-интерполяции. Известно значение интегрируемой функции в дискретных точках (узлах).
Пример: вычислить интеграл от таблично заданной функции
x |
1 |
1.4 |
1.8 |
2.2 |
2.6 |
3 |
3.4 |
3.8 |
4.2 |
4.6 |
5 |
|
1.6487 |
1.3771 |
1.1972 |
1.0833 |
1.0202 |
1 |
1.0202 |
1.0833 |
1.1972 |
1.3771 |
1.6487 |
-->x=1:.4:5;
-->y=exp((x-3).^2/8)//значения у в таблице получены табулированием этой функции
-->v=intsplin(x,y)
Получаем:
v =
4.7799684
Или:
-->x=[1 1.4 1.8 2.2 2.6 3 3.4 3.8 4.2 4.6 5];
-->y=[1.6487 1.3771 1.1972 1.0833 1.0202 1 1.0202 1.0833 1.1972 1.3771 1.6487];
-->v=intsplin(x,y)
v =
4.7799328
Способ 2.
С помощью команды inttrap. Интегрирование экспериментальных данных с помощью трапецеидальной интерполяции (метод трапеций).
При вычислении интеграла между соседними узлами функция интерполируется линейно. Этот метод вычислений называется методом трапеций.
Вычислим интеграл от той же самой функции
-->x=1:.4:5;
-->y=exp((x-3).^2/8)
-->v=inttrap(x,y)
Получаем:
v =
4.8017553
Способ 3. С помощью команды integrate. Это интегрирование по квадратуре. Может задаваться требуемая точность вычислений.
Синтаксис [x]=integrate(expr,v,x0,x1 [,ea [,er]])
Параметры
expr : подынтегральная функция;
v : переменная интегрирования;
x0, x1 : пределы интегрирования;
ea, er : действительные числа. Первое из них – еа - предельная абсолютная ошибка. По умолчанию принимает значение 0. Второе - er -, - предельная относительная ошибка. По умолчанию принимает значение 1.d-8.
Пример:
вычислить
.
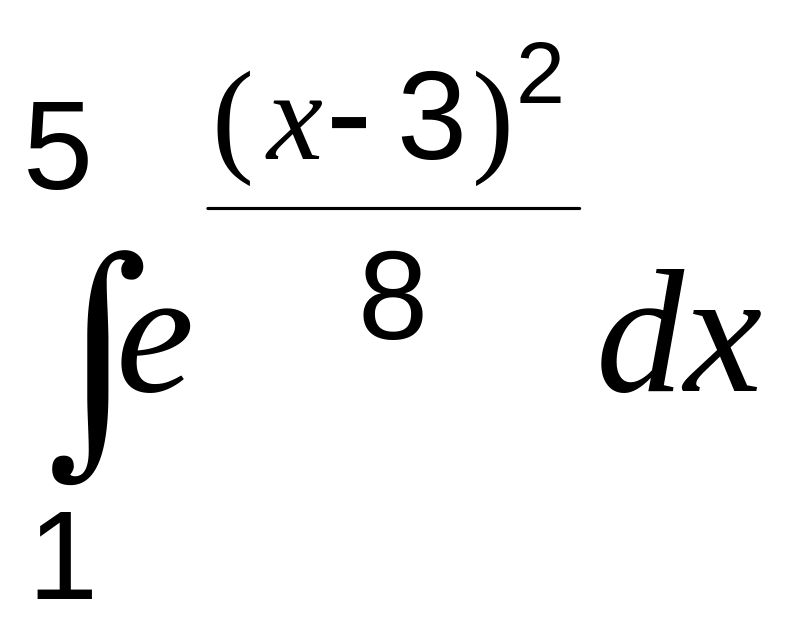-->integrate('exp((x-3)^2/8)','x',1,5)
ans =
4.7798306
Можно это сделать и так.
Набираем и сохраняем в окне редактора под именем a.sci файл
function g=a(x)
g=exp((x-3).^2/8);
endfunction
Загружаем этот файл в среду Scilab (Load into Scilab).
Далее в строке ввода набираем:
-->integrate('a','x',1,5)
Получаем:
ans =
4.7798306
Способ 4.
С помощью команды intg. Интегрируемая функция задана извне: либо в виде набора дискретных точек, либо вычисляется с помощью внешней подпрограммы. Может задаваться требуемая точность вычислений.
Синтаксис
[v,err]=intg(a,b,f [,ea [,er])
Параметры
a, b : действительные числа;
f : внешняя функция или список строк;
ea, er : - параметры, описанные выше;
err : оценка абсолютной ошибки результата.
Вычисляется определенный интеграл от a до b от f(t)dt.
Вычислим тот же
интеграл:
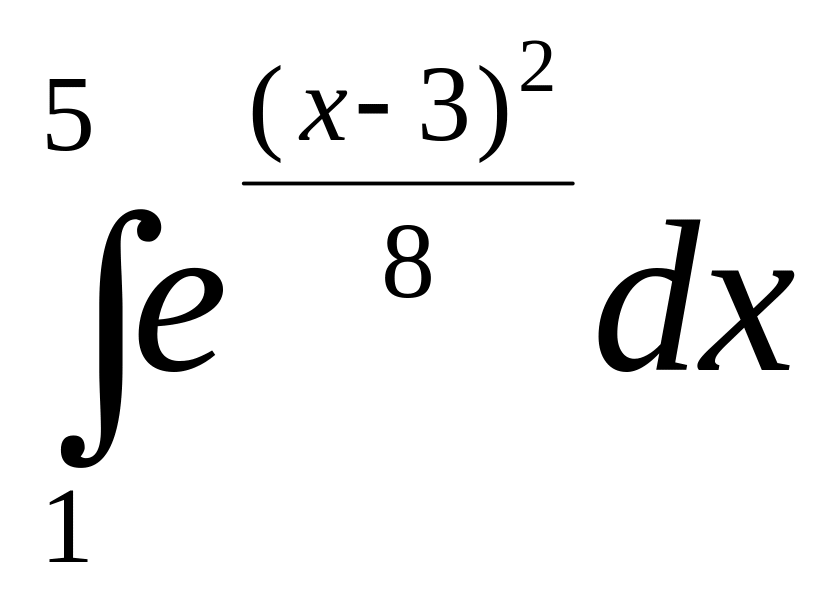
function g=a(x)
g=exp((x-3).^2/8);
endfunction
intg(1,5,a)
Вызвав этот файл на выполнение (Execute/Load into Scilab), получим ответ:
ans =
4.7798306