5.3.3. Разработка схемной модели

5.3.3.1: Вывод дифференциально-разностного уравнения. Предположим, что решение уравнения (5.3) представлено семейством кривых p(x,t), изображенным на фиг. 5.2,6. На этом ри­сунке в качестве дискретного параметра выбрано время t. Се­мейство кривых может быть параметризовано и по x, т. е. его можно представить в виде p(x_i, t ),

i= 1, 2, …, n (фиг. 5.2, а). Оба семейства кривых равноценны с точки зрения графического изображения функций p(x, t), однако при моделировании более естественно применять параметризацию по х, так как внешние

p(х,t)

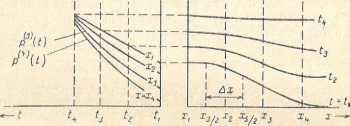
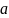
Фиг. 5.2. Представление p{x,t) семейством кривых.

воздействия прикладываются к границам областей (т. е. им со­ответствуют дискретные значения х) и являются функциями не­прерывной переменной t. Итак, будем искать решение уравне­ния (5.3) в виде семейства кривых p(x,t), которым отвечают графики на фиг. 5.2, а.

Пусть дискретные значения 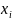выбраны эквидистантными, т. е.

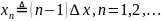
и введено следующее определение:

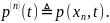
Приближенное выражение для частной производной

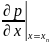
легко получить из рассмотрения фиг. 5.2, а

.

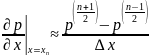Считая, что вторая производная приближенно равна разности первых производных, поделенной на , проделаем следующие выкладки:

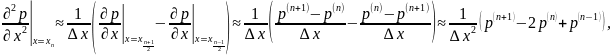
Часто применяется сокращенная запись операции приближен­ного выражения дифференциалов через разности:

,

.

В такой записи уравнение (5.3) после умножения обеих его час­тей на принимает следующий вид:

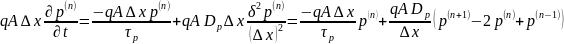, (5.4)

где частная производная по времени заменена полной производ­ной. Уравнение типа (5.4), в котором содержатся как разности, так и производные, называется дифференциально-разностным уравнением.

5.3.3.2. Схемная модель. Преимущество аппроксимации с по­мощью разностного уравнения состоит в том, что его решение можно получить с помощью схемной модели. Следуя термино­логии, принятой в работе [9], введем следующие обозначения:

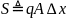— сторанта — величина, представляющая заряд в n-м элементарном слое,

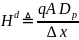—диффузанта — коэффициент, характеризующий

ток диффузии между n-м и соседними с ними слоями,

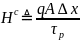— комбинанта — коэффициент, характеризующий скорость рекомбинации зарядов в n-м слое.

В случае n-го слоя уравнению (5.4) отвечает схема фиг. 5.3, если иметь в виду аналогии, указанные в табл. 5.2.

Разрешив вопрос об общем виде схемной модели, необходимо рассмотреть способ связи ее с внешними контролируемыми па­раметрами цепи (напряжением v и током i). Таблица 5.2

Моделирование диффузии при помощи линейной RG-схемы

Избыточная концентрация носителей р(n)	Напряжение узла
Сторанта	Емкость
Диффузанта	Проводимость
Комбината	Проводимость

Если рассматри­вать модель слоя как некоторую самостоятельную однокаскадную схему, тогда все связи этого каскада нужно осуществлять через его зажимы в точках 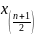, 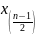. Однако разностное уравнение содержит p⁽ⁿ⁾ и «средний» ток слоя, очевидно, соответствует току № на схеме фиг. 5.4, а.

Ф и г. 5.3. Один каскад приближенной электрической модели.

Таким образом, можно считать, 4f6 граничные условия реализуются либо на стыке со­седних слоев, либо в центре слоя. Хотя, согласно работам [9, 10], можно выбрать любой способ реализации граничных условий, разрабатываемая нами модель лучше подходит для приложения граничных условий к центру слоя. Таким образом, задавая гра­ничные условия с помощью источника тока и источника носите­лей, мы получим схемные модели вида, изображенного на фиг. 5.4, б, в. В случае слоев неодинаковой толщины каскады соединяются между собой так, как это показано на фиг. 5.4, г.