4.11. Метод непрерывного преобразования схем с сохранением эквивалентности [18,31]

В качестве заключения в данной главе рассмотрим один ме­тод машинного проектирования схем, который, хотя и выглядит несколько академически по сравнению с мощными итерацион­ными методами, изложенными ранее, все же может служить од­ним из примеров нетрадиционного подхода к решению классиче­ских задач с помощью современных вычислительных машин.

Пусть заданы: схемная функция T(s), которая должна быть синтезирована, и начальная реализация схемы N₁. Требуется найти другую схему, эквивалентную N₁, но с другими значе­ниями параметров элементов или, может быть, имеющую струк­туру, отличающуюся от N₁. Например, если схемная функция имеет вид

(4.150)

тогда любая схема N₂ реализующая функцию

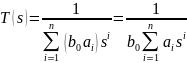, (4,151)

эквивалентна N₁ с точностью до коэффициента усиления.

Один способ получения класса схем, содержащего N₂, состоит в том, что коэффициенты а₁ берутся из множества решений

дифференциального уравнения

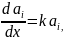
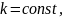
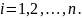(4.152)

Так как

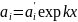(4.153)

то очевидно, что b₀= exp kx. Здесь без потери общности можно положить k=1.

Значение уравнения (4.152) состоит в том, что любое а_i мож­но записать как функцию адмиттансов элементов y_j. Раскрывая уравнение (4.152), имеем

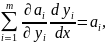
(4.154)

Или можно написать матричное дифференциальное уравнение

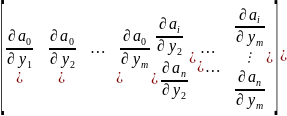
При m = n, если уравнения независимы, с помощью обращения матрицы можно найти единственные решений для .

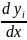П р и м е р 4.12

Фильтр, изображенный на фиг. 4.11, имеет функцию пере­дачи по напряжению (с учетом сопротивления источника R₁)

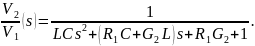
Необходимо при G₂=const и увеличении R_i сохранить функцию передачи неизменной.

Уравнения (4.152) записываются в данном случае в таком виде:

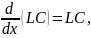
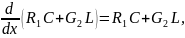
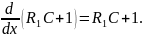
Или в матричной записи

Переходя к обычной форме записи, получаем

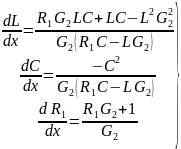(4.155)

Эти уравнения можно проинтегрировать методами численного анализа, взяв исходные значения параметров элементов схемы фильтра в качестве начальных.

Указанную методику вряд ли можно рекомендовать для боль­ших схем, поскольку при численном интегрировании нужно брать малый шаг, чтобы поддерживать точность элементов в разумных границах. Поэтому почти всегда предпочитают использовать ме­тод подбора коэффициентов. Тем не менее идея введения пара­метров сама по себе является полезной.

4.12. Заключение

Укажем некоторые направления современных исследований в области машинного проектирования радиоэлектронных схем:

1. Методы чебышевской аппроксимации частотных и времен­ных характеристик [30, 32]. Предложенные до настоящего времени методы подобного типа являются либо узко специализи­рованными, либо имеют сравнительно малые области сходимости или склонны приводить к локальному минимуму. Однако досто­инства методов чебышевской аппроксимации вполне заслужи­вают дальнейших исследований в этом направлении.

2. Оптимизация (нелинейных) переключательных и импульс­ных схем [30].

3. Автоматическая трансформация и модификация топологии схемы: исключение, замена и введение новых элементов [13, 30, 31]. Автоматический синтез топологии схемы из схем холо­стого хода и схем короткого замыкания.

ЗАДАЧИ

4.1. Показать, что в методе наискорейшего спуска направление, опреде­ленное на i-й итерации, ортогонально направлению, определенному на

(i— 1) -й итерации, если â^i-1 вычислено точно.

4.2. Флегчер и Поуэлл показывают, что их метод обеспечивает сходи­мость к А^-1 в том случае, когда минимизируемая функция квадратичная, до­казывая, что вектор 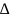x_j является линейно независимым от предыдущих (j — 1) векторов. Почему из этого следует сходимость к А^-1?

4.3. Разложение в ряд Тейлора с остаточным членом для функции n пере­менных имеет следующий вид:

,

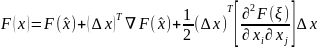где х = x — 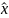, — точка глобального минимума, £ лежит на отрезке х +/Ах (О^/s^l). Доказать, что если является локальным минимумом, тогда гессиан не может быть положительно определенной матрицей на всем отрезке.

4.4. Плохую обусловленность в задачах, где функция F имеет эллипсоподобные линии постоянного уровня (как на фиг. 4.4а), можно устранить, реа­лизуя итерации не по х_i, а по log х_i . Показать на примере, как это делается.

4.5. Дополнить математическое условие унимодальности так, чтобы оно годилось для n-мерного пространства. Изобразите чашеобразный участок по­верхности, который удовлетворяет условию унимодальности, но не является выпуклым.

4.6. Можно показать, что в методе поиска с помощью чисел Фибоначчи

начальные интервалы стремятся к пределу 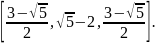Если выбрать в качестве начальных эти интервалы, то какими выражениями опи­сываются длины интервалов при последующих итерациях? Почему этот метод менее эффективен, чем изложенный в подразд. 4.4.3?

4.7. Показать, что в методе подбора коэффициентов должно выполняться следующее обязательное условие: число варьируемых элементов должно быть Не меньще числа полюсов, которые хотят сохранить на том же месте.

4,8, Высокочастотная малосигнальная модель транзистора, изображен­ная на схеме 34.1, содержит элементы у, которые зависят от тока смещения эмиттера. В частности, 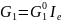, 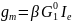(ток I_е в миллиамперах). Мы хотим компенсировать изменения, вызываемые током эмиттера, путем варьирования параметра одного или нескольких элементов. Если требуется сохра­нить два главных полюса, то сколько элементов нужно сделать варьируемыми, чтобы матрица частных производных была квадратной? Найти эту матрицу.

4.9. Пусть ограничение на элемент G выражается неравенством 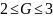. Подобрать а₁ и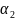 в выражении

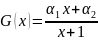так, чтобы неравенство для G выполнялось в случае х, изменяющейся в интер­вале [0,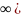 . Найти схему, реализующую G, в которой каждая проводимость

Фиг. 34.1. Полосовой усилитель.

либо постоянна, либо имеет вид G_ix. Обратите внимание на то, что для 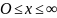итеративная схема, приведенная в подразд. 4.8.4.2, гарантирует, что G будет ограниченной величиной.

4.10 Минимизировать функцию F(x) при ограничениях

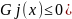
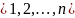с помощью метода, изложенного в подразд. 4.7.2, положив

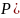
где r_k<r_k-1 . Пусть обозначает ту величину 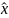, при которой P(x,r_k) достигает минимума. Показать, что F( ^k+1) <F( ^k) и . (Не обязательно требовать, чтобы функции F и G_j были выпуклой и вогнутой соответ­ственно.) Если итерации начинаются вблизи от границы G_j =0, а минимум достигается далеко от границы, то каким образом сумма 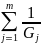может убы­вать, как это требуется?

4.11.В этой главе рассмотрен метод вычисления производных от коэффи­циентов полинома 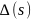который в общем случае является знаменателем не­которой схемной функции. Попытайтесь развить аналогичный метод вычисле­ний производных от коэффициентов полинома в числителе, исходя из мето­дики измерений параметров n-полюсника, аналогичной методике, отраженной на фиг. 4.15 (Указание: используйте методы вычисления частных произ­водных в частотной и временной областях, изложенные в гл. 3.) Разработайте способ рекурсивного вычисления производных от коэффициентов при помощи методов пространства состояний. (Указание: примените метод разбиений или методы теории n-полюсников, рассмотренные в гл. 1 применительно к анализу нелинейных цепей.) Следует отдельно рассматривать случаи резистивных и реактивных элементов.

4.12. Метод подбора коэффициентов имеет тесную связь с методом под­бора корней [28]. Пусть 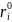— заданный (комплексный) корень; положим

F_i=r_i - (i=1, 2, …, m), тогда f_i = 0 является искомым решением. Пусть n-степень рассматриваемого полинома. Найти связь между двумя методами: а) при m =n; б) при т<n (случай главных и неглавных корней). Коэффи­циенты, естественно, подбираются с точностью до постоянного множителя. Используйте материал данной главы по чувствительности корней.