МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(национальный исследовательский университет)

«МАИ»

Учебная дисциплина

«Основы электротехники и радиоэлектроники»

КУРСОВАЯ РАБОТА

Тема: Матричный анализ линейных схем

Выполнил:

Студент Никитин Р.А.

Группа: № 4О-208Сцк

Серпухов 2015

Глава 4 оптимизация схем

Пример 4.8

Матрицу частных производных из примера 4.4 можно полу­чить, вводя источники тока, как это изображено на фиг. 4.15, Из схемы фиг. 4.15 имеем

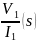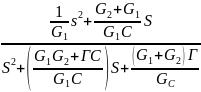= , (4.123)

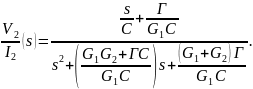(4.124)

Матрица частных производных строится из числителей выраже­ний (4.123) и (4.124)

,

(4.125)

(4.125)

что аналогично (4.86) при условии 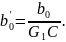Здесь, как и в

примере 4.4, выбор b'₀ не оказывает влияния на итерацию. По­этому можно положить b'₀ = 1, а 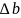'₀ вообще опустить. При этом fo (соответствующая коэффициенту при старшем члене) всегда будет равняться нулю. Коэффициенты считаются найденными, когда |f_i|< ε, i = 1, 2, . . n— 1, и на этом итерации заканчи­ваются. 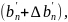В более общем случае, когда положение некоторых по­люсов безразлично, можно после каждой итерации вычислять [уравнение (4.125)] и затем нормировать эту величину делением на т. е.

И в этом случае итерации заканчиваются, когда |f_i|<ε.

При м е р 4.9 .

Активный RС-фильтр, изображенный на фиг. 4.16, в исход­ном состоянии неустойчив (главный полюс в точке s = 0,0169 ± j0,566). Следует изменить элементы схемы таким образом, чтобы главный полюс переместился в точку s = —0,05 + j1. При вычислении импедансов для всех подбираемых элементов была использована программа анализа с помощью уравнений состоя­ния. На фиг. 4.15 в скобках указаны окончательные значения параметров элементов, полученные за шесть итераций, которые заняли 4 сек машинного времени на машине IBM 360-67.

Фиг. 4.16, Схема активного фильтра. В скобках указаны значения парамет­ров элементов после корректировки главных полюсов.

4.9. Сравнение оптимизации в частотной области с оптимизацией методом подбора коэффициентов

Напомним, что при проектировании узкополосных схем для получения точных частотных характеристик нужно иметь весь­ма точные значения коэффициентов схемной функции. Частные производные от этих коэффициентов нужно знать еще точнее, так как они используются в ходе итераций при обращении ма­триц. Очевидно, наиболее точно (но зато с большими затратами времени) частные производные получаются при помощи анали­тических (символических) методов. Методами уравнений состояния производные вычисляются гораздо быстрее (но менее точно). Сейчас принято считать на основании опытных данных, что символические методы предпочтительнее при вычислениях с обычной длиной слова (8 значащих цифр), а численные (ма­тричные) методы — при вычислениях с удвоенной точностью. И в том, и в другом случае сложность схемы обычно ограничена 25 элементами и 15 узлами, так как большая часть машинного времени уходит на получение коэффициентов схемной функции и их производных, которые перевычисляются при каждой ите­рации путем обращения матрицы, [s I — А]. (Альтернатива состоит в обращении рациональной матрицы методом, аналогичным из­ложенному в гл. 3.)

Итак, может сложиться впечатление, что оптимизация в ча­стотной области обладает неоспоримыми вычислительными пре­имуществами, так как при помощи методов гл. 3 перевычислить частные производные совсем несложно. Вернемся, однако, к за­даче об оптимизации фильтра с потерями, сформулированной в начале данной главы. Как показано в работе [28], коэффициен­ты знаменателя функции передачи по напряжению V₂(s)/V₁ (s) можно с точностью до константы сделать равными коэффициен­там знаменателя функции передачи идеального фильтра (без потерь), сохраняя заданное соотношение между элементами LC (аналогично тому, как это делается в примере 4.5). Таким образом, удалось подобрать коэффициенты со значительно более высокой точностью, благодаря чему характеристика фильтра оказалась почти идеальной. Превосходство этой характеристики над характеристикой схемы, полученной при оптимизации в ча­стотной области, проявляется в том, что: 1) подбором коэффи­циентов удалось устранить проблему локального минимума, то­гда как полученная при оптимизации в частотной области ха­рактеристика, изображенная на фиг. 4.2, представляет собой как раз локальный минимум для функции ошибки F(х, ω); 2) если даже иногда удается другими методами подобрать F(х, ω), ко­торая не дает локальных минимумов, все же метод подбора ко­эффициентов требует от проектировщика значительно меньше труда и изобретательности при выборе различных функций ошибок.

Резюмируя сказанное здесь и в разд. 4.8.1, можно утвер­ждать, что метод подбора коэффициентов является наиболее подходящим для некоторых классов хорошо обусловленных чис­ленных задач, если в распоряжении проектировщика имеются удобные способы вычисления частных производных (см. [33]).