Теория ЭСОЭ / +05 Лекция

ЛЕКЦИЯ №5.

Цель лекции №5.

Ознакомившись с лекцией №5 по электротехнике, студент должен знать:

1. формулировки всех ниже перечисленных теорем;

2. уметь пользоваться этими теоремами при решении задач.

15. Теорема линейных цепей.

1. Теорема компенсации.

В электрической цепи любой пассивный элемент можно заменить эквивалентным источником напряжения, э.д.с. которого равна падению напряжения на данном элементе E=U=IR и направлена навстречу ему.

Справедливость этого утверждения вытекает из того, что любое из слагающих падения напряжений, входящих в уравнения по второму закону Кирхгофа может быть перенесено в другую сторону уравнения с противоположным знаком, т.е. может рассматриваться как дополнительная э.д.с., направленная навстречу току.

Р ис.31. Служит иллюстрацией к доказательству теоремы компенсации.

Рис. 31. Иллюстрация к теореме компенсации.

Если в ветвь ''ab'' рис.31,а последовательно включить две равные, но противоположно направленные э.д.с. E^/=E^//=IR, то точки ''a'' и ''d'', ''c'' и ''b'' оказываются соответственно точками одинакового потенциала:

Таким образом, закоротив точки ''a'' и ''d'' и исключив, получим этот участок из ветви «ab», получим схему рис. 31,в. Ток ветви при этом не изменится.

2. Теорема взаимности (обратимости).

Если источник э.д.с. k- ой ветви E_k вызывает в ветви «n» ток I_n, то этот же источник э.д.с., будучи включенным в ветвь «n» вызовет в ветви «k» тот же ток I_k=I_n.

Рис.32. Иллюстрация к теореме взаимности.

I_n=E_kq_kn, I_k=E_nq_nk (41)

Эти выражения вытекают из формулы 27,в.

Т.к. q_kn=q_nk и E_k=E_n, то I_n=I_k.

Все пассивные линейные электрические цепи обладают свойствами взаимности (обратимости).

Электрические цепи, для которых выполняется условие q_kn=q_nk называются обратимыми цепями.

Использование метода обратимости пассивных линейных электрических цепей в ряде случаев упрощает расчеты.

Пример.

Определить величину и направление тока I₄ в цепи, воспользовавшись для расчета цепи теоремой взаимности. Внутренним сопротивлением источника пренебречь.

E₁=10B; R₁=4Ом; R₂=6Ом; R₃=4Ом; R₄=1,8Ом; R₅=1Ом.

Решение:

Использование теоремы взаимности позволяет преобразовать сложную исходную цепь рис.1 в простую рис.2.

Простой цепь оказалась потому, что узлы «d» и «b» после переноса источника в ветвь c-d, связанные между собой проводом без сопротивления, слились в один узел. Следовательно, сопротивления R₁ и R₂ соединены параллельно. Так же параллельно соединены сопротивления R₃ и R₅.

На рис.3 эта же цепь изображена наглядно:

Эквивалентное сопротивление:

Ток

Токи I₁^/ и I₅^/ найдем по правилу плеч:

Ток

Но ток I^/ в схеме рис.2 после переноса источника в четвертую ветвь, согласно теореме взаимности, должен быть равен току I₄ в схеме рис.1 до переноса этого источника:

I₄=I^/=0,4(A)

Следует обратить внимание на то, что направление э.д.с. на рис.2 выбрано совпадающим с положительным направлением тока этой ветви до переноса э.д.с. При этом положительное направление тока I^/ на рис.2 должно совпадать с направлением э.д.с. в этой ветви до переноса источника.

Метод взаимности основан на теореме взаимности.

3. Теорема об эквивалентном источнике.

С помощью этой теоремы сложная электрическая схема с произвольным числом источников электрической энергии приводится к схеме с одним источником. Благодаря этому расчет электрической цепи упрощается.

Существует два варианта теоремы об эквивалентном источнике: вариант с источником напряжения и вариант с источником тока.

Теорема об эквивалентном источнике напряжения.

По отношению к зажимам произвольно выбранной ветви оставшаяся активная часть цепи (активный двухполюсник) может быть заменена эквивалентным генератором. Параметры генератора: его э.д.с. E_экв. Равна напряжению на зажимах выделенной ветви при условии, что эта ветвь разомкнута, т.е. E_экв.=U_xx; его внутренне сопротивление r₀ равно эквивалентному сопротивлению пассивной электрической цепи со стороны зажимов выделенной ветви.

Рис.33. Иллюстрация к теореме об эквивалентном

источнике напряжения.

Эквивалентная схема – схема Гемгольца-Тевенина.

Данная теорема доказывается следующим образом: в ветвь ab две одинаковые по величине и противоположно направленные э.д.с. E₁=E₂ при условии, что они равны напряжению холостого хода между зажимами a-b: E₁=E₂=U_xx.

В соответствии с принципом наложения определяем ток I_k как сумму двух токов: I_k, возникающего под действием э.д.с. E₁ и всех источников оставшейся части схемы, и тока I_k^//, возникающего от независимого действия источника E₂.

Ток I_k^/=0, т.к. E₁=U_xx

Ток I_k^/=I_k в эквивалентной схеме, называемой схемой Гемгольца-Тевенина равен

(42)

где r₀- эквивалентное сопротивление всей пассивной цепи П.

Теорема об эквивалентном источнике тока.

Ток в любой ветви «a-b» линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником тока. Ток этого источника должен быть равен току между зажимами a-b закороченными накоротко, а внутренняя проводимость источника тока должна равняться входной проводимости пассивной электрической цепи со стороны зажимов «a» и «b» при разомкнутой ветви «ab».

Рис.34 иллюстрирует эту теорему.

Рис.34

Действительно, из условия эквивалентности источников тока и напряжения следует: источник напряжения э.д.с. которого равна U_xx, а внутренне сопротивление равно r₀ может быть заменен источником тока:

(43)

J_экв., определенное по формуле (43), является током короткого замыкания, т.е. током, проходящим между зажимами «a-b», замкнутыми накоротко.

Искомый ток ветви «k» равен:

(44)

где .

Методы решения задач, основанные на теоремах об эквивалентном источнике напряжения и об эквивалентном источнике тока, называются соответственно методом эквивалентного генератора и методом эквивалентного источника тока.

Эти методы используются в тех случаях, когда по условию задачи требуется рассчитать ток только одной ветви электрической цепи.

Порядок расчета задачи методом эквивалентного генератора:

1. разрывают выделенную ветвь схемы и путем расчета оставшейся части схемы одним из методов определяют U_xx на зажимах разомкнутой ветви;

2. определяют r₀ (внутренне сопротивление эквивалентного источника) по отношению к зажимам выделенной ветви методом эквивалентных преобразований.

При этом обязательно изображается пассивная схема, где источники э.д.с. заменяются их внутренними сопротивлениями (если э.д.с. - идеальная, то участок ее подключения изображается короткозамкнутым), источники тока заменяются их внутренними проводимостями (ветви с идеальными источниками тока разрываются);

3. Определяют ток выделенной ветви по закону Ома:

.

Параметры эквивалентного генератора для реальной цепи могут быть получены на основе опытов холостого хода и короткого замыкания. Из опыта x.x. определяют U_xx, а из опыта к.з. – I_k.з. Внутреннее сопротивление источника: .

П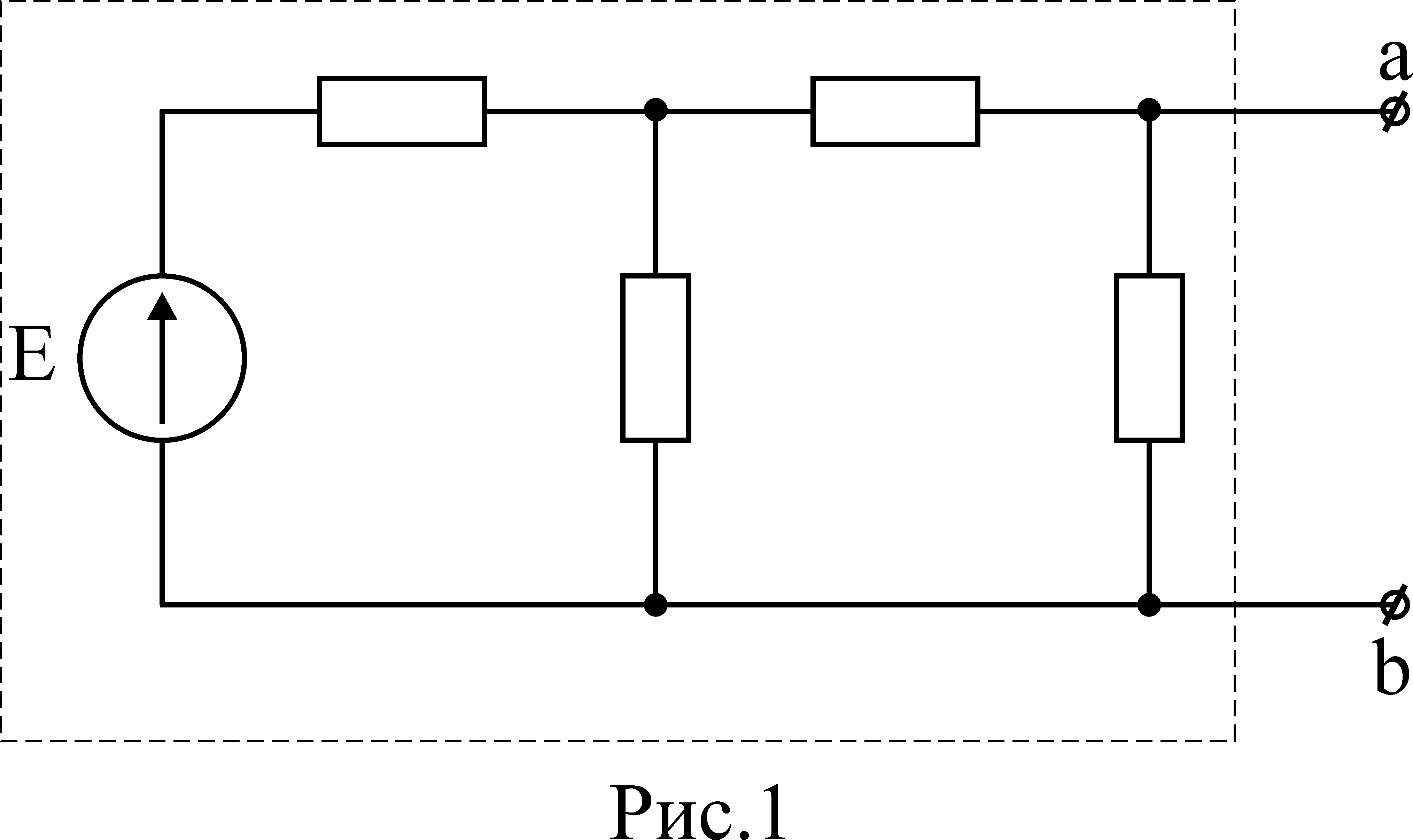ример: В цепи, изображенной на рис.1 измерено напряжение между зажимами a-b вольтметром с весьма большим сопротивлением: U_a-b=60B. Затем между зажимами a-b включили амперметр, сопротивлением которого можно пренебречь, ток, показанный амперметром I=1,5A. Сколько покажет вольтметр с сопротивлением R_V=760(Ом), если его включить между зажимами a-b?

Решение: Решим задачу методом эквивалентного генератора. Генератором будем считать цепь, очерченную пунктиром. Пусть это будет генератор напряжения. Э.д.с. этого генератора, равная напряжению холостого хода, измерена вольтметром с большим внутренним сопротивлением. Следовательно E_экв.=60B. Ток короткого замыкания показал амперметр: I_к.з.=1,5A. Но ток короткого замыкания ограничен только внутренним сопротивлением генератора. Следовательно, его внутренне сопротивление:

Если теперь к зажимам a-b подключить сопротивление R_V=760(Ом), ток через это сопротивление будет равен:

А падение напряжения на этом сопротивлении:

U=IR_V=57(B).

Это напряжение покажет второй вольтметр.

Решим задачу, выбрав в качестве эквивалентного генератора генератор тока:

П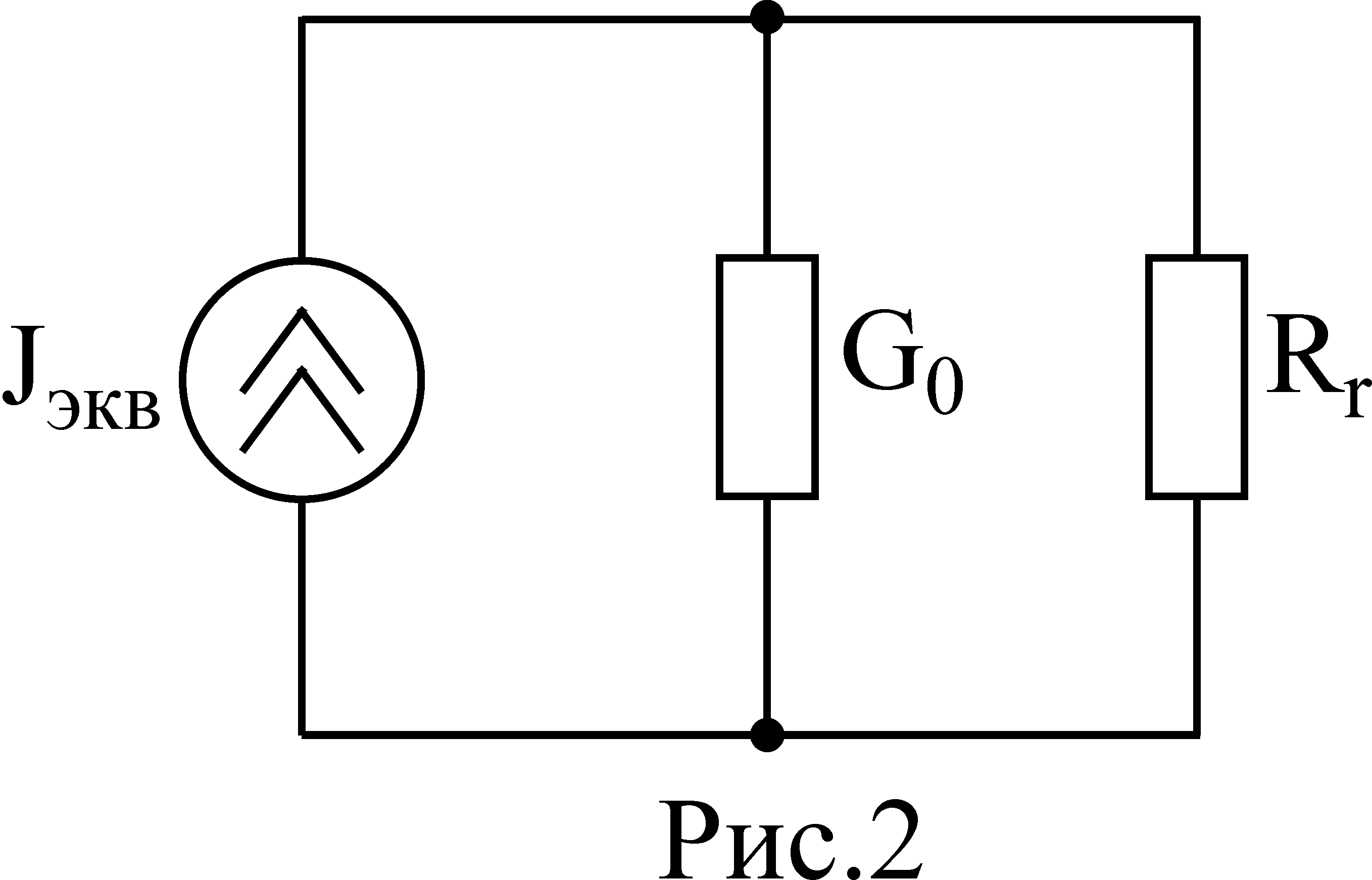араметрами генератора тока являются его задающий ток J_экв. И внутренняя проводимость G₀. Задающий ток может быть измерен или определен как ток короткого замыкания: J_экв.=J_к.з.=1,5(A).

Внутренняя проводимость может быть определена из опыта холостого хода, т.к. в этом опыте ток генератора замыкается только через G₀:

Эквивалентная проводимость цепи при подключенном вольтметре равна:

Напряжение между зажимами генератора при подключении второго вольтметра:

Контрольные вопросы.

1. Изложить суть метода взаимности.

2. В каких случаях целесообразно применить метод взаимности?

3. Привести пример применения теоремы компенсации.

4. Изложить суть метода эквивалентного источника для расчета цепей.

5. Когда наиболее целесообразно применять метод эквивалентного источника?