Теория ЭСОЭ / +Комплексный метод расчета электрических цепей

Комплексный (символический)

метод расчета электрических цепей

при периодическом синусоидальном воздействии.

Из курса "Математики" известно, что комплексное число можно представить в виде вектора на комплексной плоскости, а действительная и мнимая части комплексного числа есть проекции вектора на вещественную и мнимую оси.

(В электротехнике, т.к. буква i изображает ток, за признак мнимости принята буква j, а само число или сверху точка, или снизу подчеркнуто , ).

;

А – модуль;

– аргумент или фаза.

Если допустить, что вектор А на комплексной плоскости вращается против часовой стрелки с угловой скоростью , то это комплексное число запишется:

Величину назвали – оператор вращения.

Можно видеть, что мгновенное значение периодического синусоидального тока и напряжения , похоже на мнимую часть нашего вращающегося комплексного числа, т.е. можно утверждать:

,

.

Комплексное число назвали комплексной амплитудой тока, а – комплексном действующего значения тока.

Комплексное число назвали комплексной амплитудой напряжения, – комплексом действующего значения напряжения (как мы помним , ).

Можно видеть, что мгновенное значение периодического синусоидального тока и напряжения есть мнимая часть произведения комплексной амплитуды тока или напряжения на оператор вращения .

Пример:

А, А, А.

; , В.

Таким образом, реальные мгновенные значения синусоидального тока и напряжения мы можем заменить неким символом – комплексной амплитудой или комплексом действующего значения тока и напряжения, помня все время об операторе и (отсюда и название метода – комплексный или символический).

Посмотрим на расчете простейшей электрической схемы, что нам это даст.

Последовательное соединение R, L, C.

По 2-му закону Кирхгофа:

(1)

Тогда (1) можно записать:

(2)

В математике давно доказано, что операции над мнимыми частями комплексных чисел равноценны операциям над комплексным числом с выделением из результата мнимой части.

Тогда (2) примет вид:

Решили данное уравнение:

.

Видим, что на можно сократить, и помня, что , , , в результате получим:

где – назвали комплексным сопротивлением,

–комплексным индуктивным сопротивлением,

–комплексным емкостным сопротивлением,

–комплексным реактивным сопротивлением (знак  показывает, какое сопротивление больше – индуктивное или емкостное).

Следует помнить: , , , , .

В результате получим, что нашу исходную схему с реальными мгновенными синусоидальными токами и напряжениями можно заменить схемой с комплексным сопротивлением , в которой есть комплексные амплитуды или комплексы действующих значений токов или напряжений.

,

Получили закон Ома в комплексной форме, а также переход от комплексной величины тока и напряжения к мгновенному значению имеет только одно решение, можно записать законы Кирхгофа в комплексной форме:

1-й закон (в узле электрической цепи)

2-й закон (в замкнутом контуре цепи)

\

.

Используя при расчетах схемы с комплексными сопротивлениями, комплексами токов и напряжений мы от интегрально-дифференциальных уравнений для мгновенных значений токов и напряжений в реальной схеме, имеем уравнения обычной алгебры, но с комплексными числами. В этом основное преимущество данного метода.

Комплексное число всегда можно представить в виде вектора на комплексной плоскости. Диаграмма, отражающая совокупность векторов токов и напряжений с учетом их фаз по 1 и 2 законам Кирхгофа на комплексной плоскости называется векторной диаграммой (она широко используется при расчетах).

Для нашей схемы:

,

(надо помнить, что )

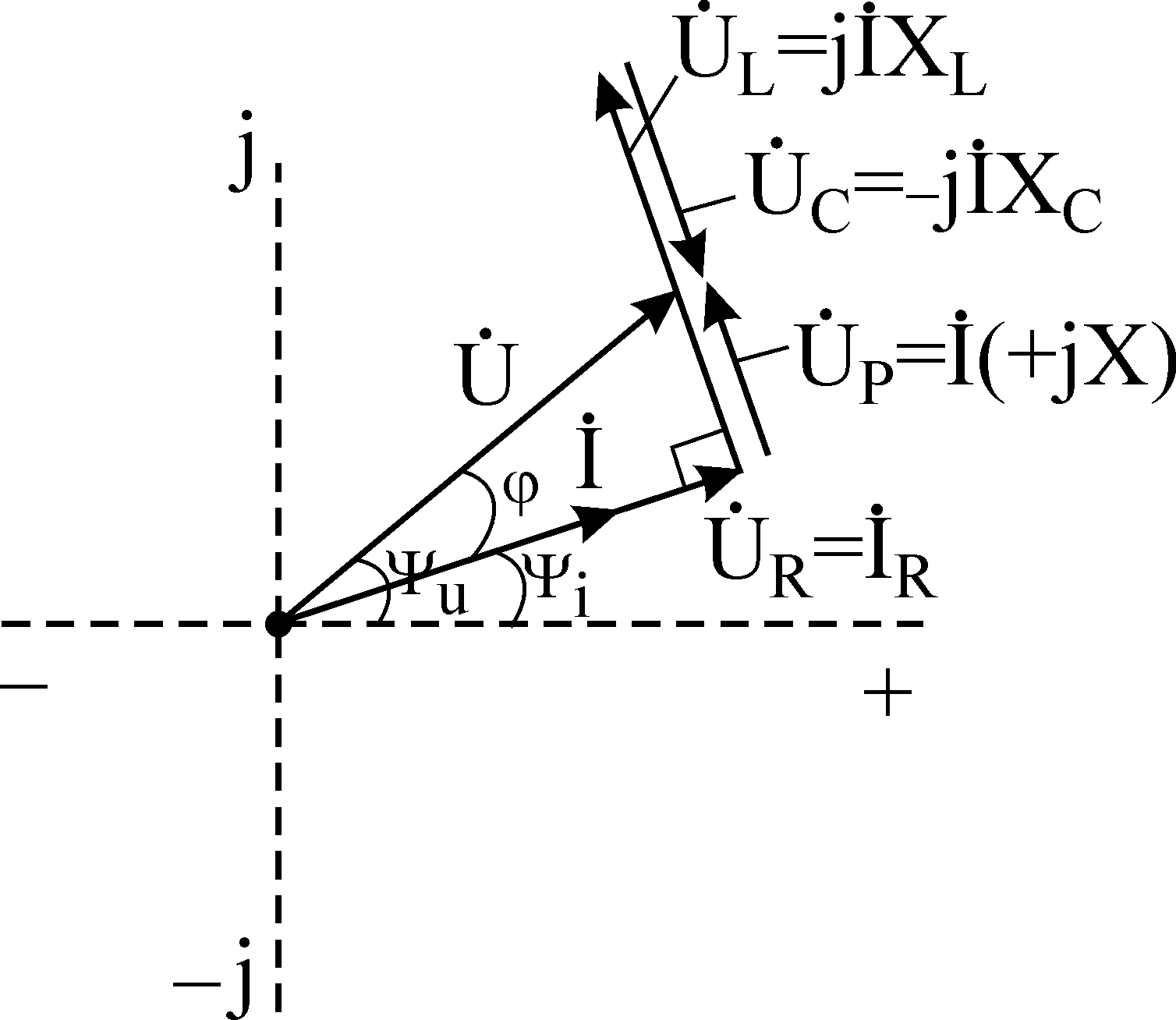
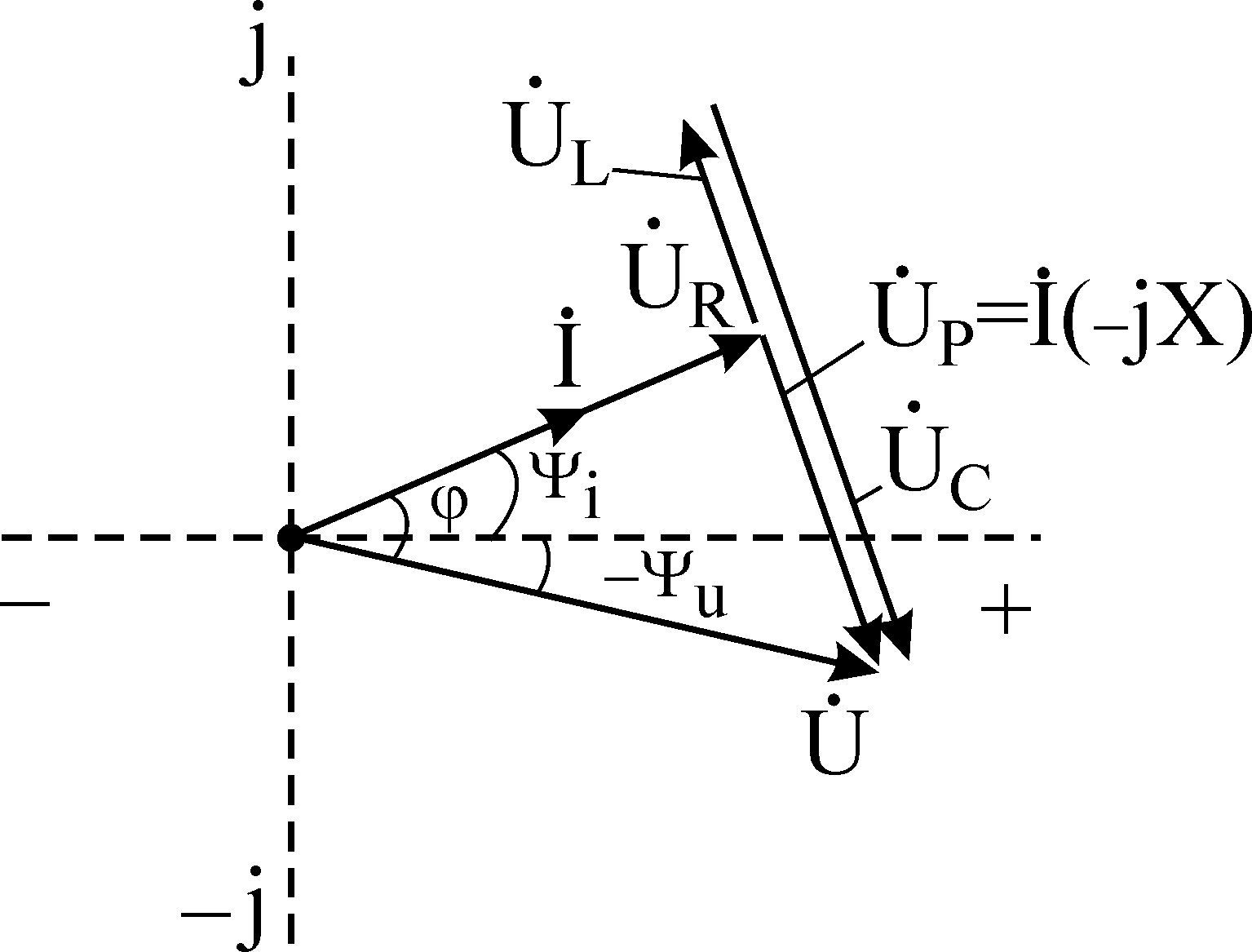
Параллельное соединение R, L, С.

Примем

Оперируем комплексом тока и напряжения и отбросим .

,

где , , , ,

, .

– комплексная полная проводимость;

– комплексная индуктивная проводимость;

– комплексная емкостная проводимость;

– комплексная реактивная проводимость.

Связь между комплексными сопротивлениями и проводимостями:

;

;

;

;

;

;

; ;

;

; .

Комплексная мощность

За комплексную мощность приняли произведение комплекса действующего значения напряжения на сопряженный комплекс действующего значения тока (сопряженный комплекс изменен на обратный () знак прямого комплексного числа (, )).

Если , , тогда учитывая известные ранее полную мощность , активную мощность , реактивную мощность , имеем:

В электрических цепях при периодическом синусоидальном воздействии имеет место баланс мощностей источников и нагрузок, т.е. комплексная мощность источников энергии должна быть ровна комплексной мощности нагрузок и активные и реактивные мощности источников равны активной и реактивной мощностям нагрузок.

,

, ,

, .

Знак реактивной мощности означает преимущество индуктивного (+) или емкостного (–) сопротивлений.