1. Источник сообщений выдает символы из ансамбля . Распределения вероятностей приведены в таблице 1. Найти количество информации, содержащееся в каждом из символов источника при их независимом выборе (источник без памяти). Вычислить энтропию и избыточность заданного источника.

Таблица 1

Вариант
г)	0,4	0,25	0,05	0,3	-	-	-	-

Количество информации в передаваемом символе определяется в битах. Чем меньше вероятность появления того или иного символа, тем больше количество информации извлекается при его получении. Если источник может выдать один из двух независимых символов (а₁ и а₂) и первый из них выдается с вероятностью р(а₁)=1, то символ а₁ не несет информации, ибо он заранее известен получателю.

Количество информации определяется выражением:

I(a_i)=log₂1/p(a_i)= -log₂p(a_i).

I(a₁)= -log₂0,4 = 1,3;

I(a₂)= -log₂0,25= 2;

I(a₃)= -log₂0,05= 7,64;

I(a₄)= -log₂0,3= 1,73;

Энтропия – это среднее количество информации Н(А), которое приходится на один символ:

где: a_i - символ выдаваемый источником сообщений;

K – объём алфавита;

H(A)= 1,773 бит/симв.

Избыточность источника зависит как от протяженности статистических связей между последовательно выбираемыми символами, так и от степени неравно вероятности отдельных символов.

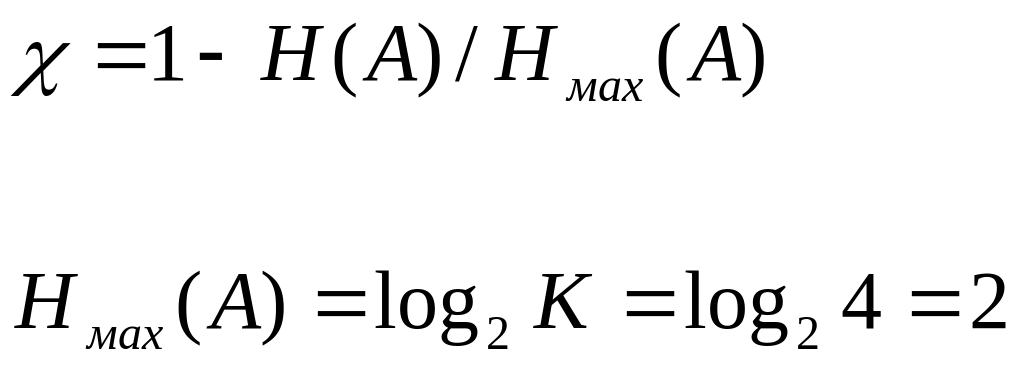
1.6. Сообщения, составленные из букв русского алфавита, передаются в коде МТК-2 при помощи стартстопного телеграфного аппарата. В начале передачи идёт стартовая посылка, а в конце – стоповая. Буква передаётся пятью элементарными посылками длительностью ₁ = 20 мсек. Длина стартовой посылки ₂ = 20 мсек, стоповой - ₃ = 30 мсек. Определить:

а) скорость передачи информации;

Вероятность появления стартовой посылки: p₁=1/7;

Вероятность появления элементарной посылки: p₂=5/7;

Вероятность появления стоповой посылки: p₃=1/7;

Скорость передачи информации для взаимно независимых символов, имеющих разную длительность:

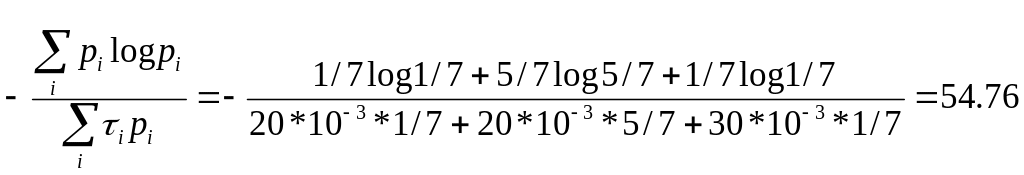симв/с.

1.17(Г). Определите пропускную способность канала (рис.1). Символы на входе канала считать равновероятными.

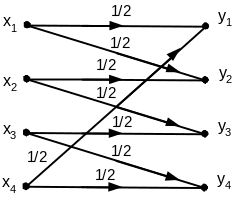
Рисунок 1

Пропускная способность канала связи , бит/симв:

log K=log4 =2; - =-[ ]=

=p(x₁)p(x₁|y₁)log(x₁|y₁)+ p(x₁)p(x₁|y₂)log(x₁|y₂)+ p(x₂)p(x₂|y₂)log(x₂|y₂)+p(x₂)p(x₂|y₃)log(x₂|y₃)+

+p(x₃)p(x₃|y₃)log(x₃|y₃)+ p(x₃)p(x₃|y₄)log(x₃|y₄)+p(x₄)p(x₄|y₄)log(x₄|y₄)+ p(x₄)p(x₄|y₁)log(x₄|y₁)=

=0,25·0,5·log0,5+0,25·0,5·log0,5+0,25·0,5·log0,5+0,25·0,5·log0,5+

+0,25·0,5·log0,5+0,25·0,5·log0,5+0,25·0,5·log0,5+0,25·0,5·log0,5=8·0,25·0,5·(-1)=-1;

=2+1=3 бит/симв.

1. Дискретный источник выдает символы из ансамбля с вероятностями, приведенными в таблице. Закодировать символы данного ансамбля кодом Хаффмена, кодом Шеннона-Фано и равномерным кодом. Определить среднюю длину кодовой комбинации и сравнить с энтропией сообщения. Показать, какой код является наиболее эффективным.

Таблица 2

Вариант
г)	0,4	0,25	0,05	0,3	-	-	-	-

Код Хаффмена:

Средняя длина кодовой комбинации данного кода:

Код Шеннона-Фано:

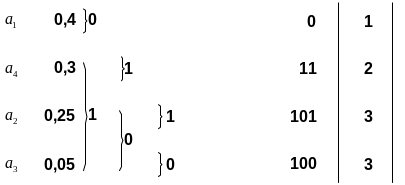
Средняя длина кодовой комбинации данного кода:

Равномерный код:

Число разрядов в кодовых комбинациях равно n=log4=2

Граф двухразрядного двоичного кода:

Символ	Разложение числа по основанию 2	Кодовые комбинации
а1	0*21+0*20	00
а2	0*21+1*20	01
а3	1*21+0*20	10
а4	1*21+1*20	11

Рисунок 2

Кодовые комбинации:

Таблица 3

Средняя длина кодовой комбинации будет равна 2.

При оптимальном двоичном кодировании средняя длинна кодовой комбинации, должна равняться энтропии сообщения т.е.;

= 1,921(бит/символ),

Сравним среднюю длину кодовых комбинаций с энтропией сообщения;

Код Шеннона – Фано: = = 7,16%;

Код Хаффмена = = 7,16%;

Равномерный код = = 12,8%;

Вывод: Наиболее эффективным кодом для кодирования данного источника являются код Хаффмена и код Шеннона – Фано.

2.4. Найти код Лемпела-Зива для двоичной последовательности источника:

г) 110000011000001;

1. Последовательность с выхода дискретного источника делятся на блоки переменной длины, которые называются фразами.

2. Каждая новая фраза должна отличаться от всех предыдущих и в одном символе от одной из предыдущих фраз.

3. Все фразы записываются в словарь, который сохраняет расположение существующих фраз.

4. Кодовые слова состоят из двух частей. Первая часть представляет собой номер словаря в двоичной форме предыдущей фразы, которая соответствует новой фразе, кроме последнего символа. Вторая часть – это новый символ, выданный источником. Первоначальный номер ячейки словаря 0000 используется, чтобы кодировать пустую фразу, т. е. «0» или «1».

Последовательность символов делится на фразы:

Номера ячеек словаря, фразы и полученные кодовые слова приведены в таблице 4.

Таблица 4

Расположение в словаре	Фразы	Кодовое слово
0001	1	0000 0
0010	10	0001 0
0011	00	0010 0
0100	001	0011 1
0101	100	0010 0
0110	0001	0101 0

1. Сообщения источника, имеющего алфавит объемом , кодируется двоичным блочным кодом. Количество разрядов в каждой кодовой комбинации . Какое число информационных и проверочных символов содержится в каждой кодовой комбинации? Сколько разрешенных и запрещенных комбинаций в используемом коде? Определить избыточность и относительную скорость кода.

Таблица 5

Вариант
г)	64	10

Для корректирующих кодов, число комбинаций N удовлетворяет неравенству:

N=mⁿ>K N = 2¹⁰ = 1024 > 32.

При этом часть кодовых комбинаций используется для кодирования, эти кодовые комбинации называются разрешенными, их число:

N_p=K=64

А другая часть при кодировании не используется. Число неиспользуемых при кодировании комбинации, называемых запрещенными, равна:

N_з=N-N_p=1024-64=960

В пятиразрядной кодовой комбинации корректирующего кода k=log₂K символов являются информационными:

k=log₂64=6.

r=n-k символов – проверочными (избыточными).

r=10-6=4.

Избыточностью равномерного блочного кода является величина:

а относительная скорость кода:

3.4. Построить порождающую матрицу для кода с минимальным кодовым расстоянием , количеством информационных элементов . Написать правила формирования проверочных элементов для полученного кода. Найти проверочную матрицу. Определить, сколько ошибок такой код может обнаружить и исправить. Нарисовать структурные схемы кодирующего и декодирующего устройства. Составить таблицу соответствия между местоположением одиночных ошибок и видом синдрома.

Таблица 6

Вариант
г)	2	4