Взам. инв. №

Подпись и дата

ТПЖА.712002.002 КР

Изм.

Кол.

Лист

№док

Подпись

Дата

Инв. № подл.

Разраб.

Зырянова

«Организация контроля качества результатов анализа в лаборатории»

Лит.

Лист

Листов

Пров.

Казиенков

2

48

Н. контр.

Кафедра ТЗБ Гр. РСП – 31

Т. контр.

Утв.

Содержание

Введение……………………………………………….…………….…….......3

1. Критерии качества результатов экоаналитических исследований …...4

   1. Погрешность………...……………………………………….……......4

1.2 Точность и правильность, повторяемость и воспроизводимость....14

2 Особенности организации внутрилабораторного контроля качества результатов анализа…………………………………………………………20

2.1 Внутрилабораторный контроль..………………………………..…...20

2.2 Оперативный контроль…………………………………………….....22

2.3 Контроль стабильности результатов анализа……………….……....25

2.3.1 Контроль стабильности при наличии стандартного образца…26

2.3.2 Контроль стабильности в условиях отсутствия стандартного образца……………………………………………………………….....27

3 Подтверждение технической компетентности лабораторий, осуществляющих контроль качества окружающей среды……………….30

3.1 Факторы, определяющие правильность и надежность………….....30

3.2 Аккредитация лабораторий………………………………………….37

Заключение…………………………………………………………………..42

Библиографический список………………………………………………...43

Приложение А……………………………………………………………….46

Приложение Б……………………………………………………………….47

Приложение В……………………………………………………………….48

Введение

Организация контроля качества результатов анализа в лаборатории очень важна для всех исследований в лабораториях, так как на ней основывается точность всех результатов.

Целью данного курсового проекта является ознакомление с организацией контроля качества результатов анализа в лаборатории. А также ознакомление с нормативно-правовым и нормативно-техническим обеспечением процесса. В данном курсовом проекте рассматриваются критерии качества результатов экоаналитических исследований, особенности организации внутрилабораторного контроля качества результатов анализа. А также разбирается подтверждение технической компетенции лабораторий, которые осуществляют контроль качества окружающей среды.

1 Критерии качества результатов экоаналитических исследований

1.1 Погрешность

Погрешность измерения (ошибка измерения) – это любое отклонение измеренного значения от ее истинного (действительного) значения. При этом истинное значение — это значение, которое идеальным образом характеризует в качественном и количественном отношении соответствующую величину.

Доверительные границы погрешности – это верхняя и нижняя границы интервала, которая с данной вероятностью захватывает погрешность измерения. То есть это наименьшее и наибольшее значения погрешности измерений, ограничивающие интервал, внутри которого с определенной заданной вероятностью находится истинное значение погрешности результата измерений

(1)

где Хизм – измеренное значение;

∆_p – доверительная граница погрешности.

Так как применяемые методы и средства измерения далеко не совершенны, то результат абсолютно каждого измерения несет в себе погрешность.

Погрешности измерений могут быть классифицированы по различным признакам.

1. По способу выражения (форме представления):

а) абсолютные погрешности;

б) относительные погрешности.

2. По характеру проявления:

а) систематические погрешности;

б) случайные погрешности;

в) грубые погрешности.

Теперь рассмотрим все эти погрешности более подробно.

Абсолютная погрешность – это погрешность измерения, которая выражается в единицах измеряемой величины. Она является оценкой абсолютной ошибки измерения (испытания) и рассчитывается как разность между истинным и полученным значением.

Абсолютная погрешность рассчитывается по формуле

(2)

где А – оценка абсолютной погрешности;

И – истинное значение;

П – полученное значение.

Абсолютная погрешность не зависит от значения измеряемой величины.

Она обычно записывается со знаком ± (пример: 100±0,05) и измеряется в тех же единицах измерения, что и сама величина.

Эта погрешность не может в полной мере служить показателем точности измерений, так как одно и то же ее значение может одновременное соответствовать, и достаточно высокой, и достаточно низкой точности измерений [7].

Например: длина листа бумага формата А4 равна (29,7±0,1) см, а расстояние между Кировом и Москвой (950±0,1) км. Погрешность в первом случае будет меньше одного миллиметра, а во втором – одного километра.

Кроме абсолютной погрешности существует очень взаимосвязанная с ней относительная погрешность.

Относительная погрешность – это отношение абсолютной погрешности измерения к истинному значению измеряемой величины. Относительную погрешность можно выразить с помощью формулы

, (2)

где О – оценка относительной погрешности.

Относительная погрешность является безразмерной величиной, но её численное значение может указываться, например, в процентах. Тогда формула приобретает вид

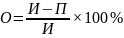(3)

Относительная погрешность зависит от значения измеряемой величины, так как она непосредственно отнесена к этому измеренному значению [7].

В качестве примера продолжим разбирать предыдущий пример, рассчитывая погрешность листа бумаги. В первом случае (с листом бумаги) мы получим

А при расчете расстояние между городами

И так мы видим, что расстояние между городами измерено точнее, чем длина листа формата А4.

Тут можно говорить сразу и о роли абсолютной погрешности (так как одно и то же ее значение применимо к разным величинам, но при этом результат разный), и об относительной погрешности

По характеру проявления погрешности делятся на случайные, систематические и грубые.

Случайная погрешность – это разброс, который характеризует случайные изменения в серии повторных измерений одной и той же величины, проводимых в одинаковых условиях [7].

Источником этой погрешность является неопределенность результатов, которые могут быть персонального, инструментального или методического происхождения [7]. Примером персонального происхождения может служить, к примеру, разное цветовое восприятие людей, а методического – факт того, что в методике рассчитывают на идеальные условия, которые в жизни могу быть просто невоспроизводимы.

В появлении случайных погрешностей не наблюдается какой-либо закономерности, они выявляются при повторных измерениях одной и той же величины в виде небольшого разброса получаемых результатов. То есть, если рассматривать этот же фотоколориметр, то выявить случайную погрешность будет возможно только при проведении нескольких опытов. Каждый раз результаты будут похожи друг относительно друга, но все же будут отличаться на определенное значение. Это и будет случайной погрешностью.

Случайные погрешности, как правило, возникают из-за одновременного влияния многих независимых причин, каждая из которых в отдельности слабо влияет на результаты испытаний. Таким образом, случайные погрешности могут быть связаны с особенностями приборов и объекта измерений (пример: при определении диаметра тонкой проволоки, может оказаться, что ее сечении вовсе не круглое).

Величина разброса определяется как качеством работы оператора, так и качеством применяемой методики. Степень близость друг к другу отдельных значений в серии результатов повторных (параллельных) измерений, то есть степень разброса данных относительно среднего, называется воспроизводимость (для параллельных – повторяемость), которые будут рассмотрены ниже. Но пока можно сказать, что случайные погрешности определяют воспроизводимость [7].

Случайная погрешность оценивается из серии параллельных измерений. Все полученные результаты, как правило, будут отличаться друг от друга. Простейшая операция, которую можно провести над этими данными – усреднение, например, путем вычисления среднего арифметического

(4)

где n – серия независимых испытаний [7].

Случайные погрешности присутствуют всегда, они неустранимы, но их влияние всегда можно снизить за счет аккуратности в работе и простой статической обработкой результатов, то есть увеличением числа параллельных измерений. Эту ситуацию можно опять же встретить при работе с фотоколориметром: если каждое измерение прибор будет проверяться на точность установки (то есть настраиваться на ноль), то случайная погрешность сводится к минимуму.

Систематическая погрешность – это часть погрешности измерения, остающаяся постоянной или же закономерно изменяющаяся при повторных измерениях одной и той же величины. Количественно данная погрешность характеризуется как разность между средним и истинным значениями. В зависимости от характера измерения систематические погрешности подразделяют на постоянные и переменные.

Постоянные погрешности – это погрешности, которые длительное время не изменяют свое значение, например, в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто. Пример: неправильная градуировка, неправильная установка отсчета.

Переменные погрешности - погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора. Пример: временное изменение температуры. [17]

Источником систематической погрешности может быть как лабораторная погрешность, так и погрешность методики. Погрешность методики можно разобрать на примере методик по почвоподготовке. Во многих методиках по определению различных характеристик почв, нужно подготовить почвенную вытяжку. Методики описывают как это делать, но не учитывают, что часть вещества, содержащаяся в почве, не попадает в почвенную вытяжку, что может существенно повлиять на качество результатов. Таким образом, у этой методики всегда присутствует систематическая погрешность, при чем, также будет присутствовать и случайная, так как каждый раз в почвенную вытяжку будет попадать разное количество веществ, которое удастся вымыть из почвы.

Также подобное влияние можно встретить в титровании. Как известно, последняя капля всегда будет лишней, но без нее не определить, что вещество оттитровано, поэтому оператор всегда будет определять не точное количество вещества.

Систематические погрешности в зависимости от причин классифицируют:

1. погрешности метода (теоретические погрешности), которые связаны с недостаточной проработкой теории методических указаний измерений, а также могут быть связаны с упрощениями при проведении анализа;

2. инструментальные погрешности, обусловленные неправильной установкой средств измерений (пример: неправильная настройка длины волны в фотоколориметре);

3. персональные погрешности, которые обусловлены индивидуальными особенностями наблюдателя (пример: запаздывание или опережение при регистрации сигнала, разное восприятие цветовой гаммы).

Чаще всего систематические погрешности могут быть связаны с ошибками приборов, которые не были учтены экспериментатором до проведения анализа. Систематические погрешности подлежат исключению насколько возможно. Наиболее известный способ это введение поправок на известные систематические погрешности, в ходе которой в результат измерения вносят поправки, которые равны этим погрешностям, но с обратным знаком. Однако исключить эту погрешность до конца практически невозможно, хотя бы потому, что условия измерения, а значит и условия возникновения систематических ошибок постоянно изменяются.

Систематические погрешности могут быть выявлены и уменьшены, а при возможности и полностью устранены [7].

Также необходимо учесть, что в условиях параллельных измерений главная задача выявление и оценка. А исключение в таких случаях чисто техническая задача: откалибровать прибор, например, или приготовить заведомо перетитрованный раствор для сравнения.

При этом систематическую погрешность нельзя выявить и оценить повторными измерениями, потому, что, например, если ее исключить введением поправки, то случайные отклонения погрешности от значений все равно останутся не исключенными. Такое случайное по характеру различие значений систематической погрешности при повторении измерения, которое невозможно исключить, называют остаточным действием систематической погрешности.

Грубая погрешность (промах) - это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Причины грубой погрешности, как привило, происходят из-за следующих возможных факторов:

- неправильных действий оператора, в том числе его ошибки (неверные записи, вычисления, неверный отсчет, неправильное обращение с приборами и т.д.);

- сбоя технических средств;

- кратковременных резких изменений условий измерения.

Грубые погрешности обязательно должны быть исключены, после обнаружения.

Также необходимо отметить, что классификация погрешностей на случайные и систематические очень условно. Примером может послужить ошибка округления, которая может носить как систематический, так и случайный характер.

Очень важно отметить два следствия из всех погрешностей:

1. чем меньше измеряемая величина, тем больше погрешность (пример с листом бумаги и расстояние между городами);

2. чем больше размер измеряемой величины, тем меньше погрешность. Это следствие из верхнего: чтобы снизить величину погрешности, нужно увеличивать измеряемые величины. Здесь можно привести пример разбавления в 500 раз. Это можно сделать многими способами, самый простой из которых – взять аликвотную часть в 1 мл и довести дистиллированной водой до метки мерной колбы. А более правильно будет то, что мы, отобрав аликвотную часть 1 мл, сначала разбавим в 50 раз, а далее из этого раствора отберем 10 мл и разбавим их еще в 10 раз.

Для подтверждения этого фактора можно привести в пример ситуацию с лупой. Можно взять лупу, которая увеличивает предмет в 2 раза, и лупу, которая увеличивает в 4 раза. Мы можем рассмотреть предмет и в более слабую лупу, но более точное изображение мы получим, если возьмем лупу, увеличивающую в 4 раза.

Также существует понятие общей погрешности. Это сумма случайной и систематической погрешности. Сюда не входит грубая погрешность, так как они, как было сказано выше, должны быть обязательно исключены после обнаружения. Чем меньше общая погрешность, тем выше точность измерений.

Необходимость в общей погрешности заключается во том, что измерения, выполняемые на предположительно идентичных материалах при предположительно одинаковых условиях, не дают, как правило, похожих результатов. Это зависит от влияния многих факторов на результат измерения, не поддающимся полному контролю, так как включают в себя целый спектр различных условий. К таким факторам относится температура, давление, освещение, погрешность применяемого оборудования, качество используемых реактивов и многое другое, в том числе многообразный человеческий фактор [15].

При этом при практическом объяснении результатов измерений эта изменчивость должна быть всегда учитана. К примеру, нельзя учитывать фактическое различие между полученным результатом измерений и какой-либо точной величины, если она лежит в области неизбежных случайных погрешностей измерительной процедуры, которые представлены в таблицах в начале методик по проведению измерений.

Таким же образом, сопоставление результатов испытаний двух существенно различающихся проб материала не выявит какого-либо серьезного отличия в качестве, если расхождение между результатами лежит в вышеупомянутой области.

Обобщенной характеристикой средств измерения является класс точности. Это характеристика прибора, которая определяет допустимые значения всех погрешностей, которые непосредственно влияют на точность. То есть класс точности описывает максимально возможную погрешность прибора. Самый точный класс – первый. Чем меньше класс точности, тем меньше точность прибора и больше погрешности, получаемые при использовании этого средства измерения.

Для стрелочных приборов принято указывать класс точности в виде числа. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Например, у вольтметра, который работает в диапазоне измерений 0 – 30В, класс точности 1,0 определяет, что указанная погрешность не превышает 0,3В.

Как привило, половина цены деления шкалы прибора соответствует погрешности этого прибора. И, при условии, что класс точности не известен, за погрешность прибора как раз применяют половину цены его деления [9, 10, 11].

Мерная посуда тоже имеет свои классы точности. Стоит отметить, что мерная посуда включает в себя цилиндры, мензурки, колбы, бюретки, пипетки и др. Для мерной посуды устанавливается два класса точности: первый устанавливается для более высокой точности измерений, второй – для менее точных измерений. Так, по ГОСТ 1770-74 цилиндры изготавливают 1 и 2 классов точности. В качестве примера может служить цилиндр вместимостью 250 м³, 2 класса точности. Тогда его можно записать: Цилиндр 1-250-2 ГОСТ 1770-74, где первая цифра (1) – исполнение (в данном случает 1 означает, что цилиндр изготовлен с носиком), 250 – объем цилиндра, последняя цифра (2) – класс точности [12, 14].

Пипетки с одной меткой изготавливаются по ГОСТу 29169-91 первого и второго классов точности. Они изготавливаются разной вместимостью. Для каждой вместимости и класс точности существуют предельные отклонения, зависимость которых можно наблюдать в таблице 1.

Таблица 1 – Предельные отклонения от номинальной вместимости пипеток с одной отметкой при 20˚С.

Номинальная вместимость,  см3	Предельные отклонения, см3
	1 класс	2 класс
0,5	±0,005	±0,01
1	±0,008	±0,015
2	±0,01	±0,02
5	±0,015	±0,03
10	±0,02	±0,04
20	±0,03	±0,06
25	±0,03	±0,06
50	±0,05	±0,01
100	±0,08	±0,15
200	±0,1	±0,2

Пример условного обозначения пипетки 1 класса точности, номинальной вместимости 10 см³: Пипетка 1-50 ГОСТ 29169-91 [13, 14].