4.1 Приведение масс частей кривошипно-шатунного механизма

Для упрощения динамического расчета действительный КШМ заменяется эквивалентной системой сосредоточенных масс (рисунок 4.2), которая состоит из массы m_J, совершающей возвратно-поступательное движение и сосредоточенной в точке А, и массы m_R, совершающей вращательное движение и сосредоточенной в точке В.

Сосредоточенные массы m_J, кг, и m_R, кг, определяются по формулам:

m_J = m_П + m_ШП; (4.3)

m_R = m_К + m_ШК, (4.4)

где m_П – масса поршневой группы, кг;

m_ШП – часть массы шатунной группы, сосредоточенная в точке А (на оси поршневого пальца), кг; m_ШП = 0,275  m_Ш;

m_ШК – часть массы шатунной группы, сосредоточенная в точке В (на оси кривошипа), кг; m_ШК = 0,725  m_Ш;

m_К – часть массы кривошипа, сосредоточенная в точке В.

Рисунок 4.2 – Схемы системы сосредоточенных масс, динамически эквивалентной кривошипно-шатунному механизму

Полная масса шатунной группы m_Ш, кг, равна:

m_Ш = m_ШП + m_ШК. (4.5)

Часть массы кривошипа m_К, кг, определяется по формуле

m_К = m_ШШ + 2 m_Щ  /r, (4.6)

где m_ШШ – масса шатунной шейки с прилегающими частями щек, кг;

m_Щ – масса средней части щеки, заключенная в контуре abсd, центр тяжести которой расположен на расстоянии  от оси вращения вала.

Для приближенного определения значений m_П и m_Ш следует использовать конструктивные массы m_i' (массы, отнесенные к площади поршня), значения которых представлены в [1, таблица 4.1], то есть по формулам:

m_П = m_П'  F_П = 100  0,00689 ≈ 0,689 кг; (4,7)

m_Ш = m_Ш'  F_П = 150  0,00689 ≈ 1,034 кг. (4.8)

По формуле (4.3) получаем:

m_J = 0,689 + 0,275  1,034 _≈0,973 кг.

4.2 Расчет сил инерции

Силы инерции, действующие в КШМ, в соответствии с характером движения приведенных масс (см. рисунок 4.1) подразделяются на силы инерции поступательно движущихся масс Р_J и центробежные силы инерции вращающихся масс K_R.

Значение силы Р_J , Н, определяется по формуле

Р_J = – m_J  j, (4.9)

где j – ускорение поршня, м/с². Причем:

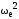
j = r  (cos  + λcos 2). (4.10)

Значение силы K_R, Н, определяется по формуле

K_R = – m_R  r . (4.11)

Центробежная сила инерции К_R является результирующей двух сил:

– силы инерции вращающихся масс шатуна К_RШ, Н, равной:

К_RШ = = – 2,23 МПа; (4.12)

– силы инерции вращающихся масс кривошипа K_RK, Н, равной:

K_RK = – m_К  r . (4.13)

Силы инерции возвратно-поступательно движущихся масс Р_J действуют по оси цилиндра и как силы давления газов, являются положительными, если направлены к оси коленчатого вала. Центробежная сила инерции K_R действует по радиусу кривошипа и направлена от оси коленчатого вала.