2.3 Определение оптимальных значений дебита и давления на забое скважины при совместной работе пласта и скважины

Точка пересечения, полученная при совместном решении уравнения работы подъёмника и уравнения притока жидкости из пласта в скважину, определяет условие совместной работы пласта и скважины, т.е. даёт дебит скважины и соответствующее ему забойное давление .

Рисунок 2.3 – График совместной работы пласта и скважины

2.4 Определение параметров фильтрации нефти к скважине Определение соблюдения закона а. Дарси

Определим выполнение закона А. Дарси при фильтрации нефти к скважине, используя найденные оптимальные значения дебита скважины Q = 240 м³/сут при давлении на забое скважины р_с = 19,22 МПа.

Для этого необходимо определить значение фильтрационного числа Рейнольдса по формуле В. Н. Щелкачева:

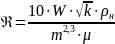, (2.29)

где W – скорость фильтрации флюида, м/с;

k – проницаемость породы, м²;

m– пористость породы, доли.

и сравнить его с интервалом критических значений - . Если вычисленное по формуле В.Н. Щелкачева число Re окажется меньше критического значения Re_кр, то закон Дарси справедлив, если число Reбольше верхнего значения Re_кр, то закон Дарси заведомо нарушен.

Скорость фильтрации можно определить по формуле:

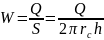. (2.30)

Подставим значения, согласно заданию и вычислим скорость фильтрации нефти:

Тогда значение фильтрационного числа Рейнольдса:

Следовательно, закон Дарси выполняется.

Построение графика распределения давления в пласте

График распределения давления в пласте получим, задаваясь различными значениями r, определяя соответствующие значения давления p по закону распределения давления. Для нахождения давления в пласте воспользуемся следующей формулой:

где – оптимальное давление на забое скважины;

r – расстояние от центра скважины до точки в пласте.

Таблица 2.3- Данные к построению графика распределения давления в пласте

1	20,13	500	22,55
5	20,75	550	22,59
50	21,65	600	22,62
100	21,92	650	22,65
150	22,08	700	22,68
200	22,19	750	22,71
250	22,28	800	22,73
300	22,35	850	22,76
350	22,41	900	22,78
400	22,46	950	22,8
450	22,51	1000	22,82

Рисунок 2.4

Построение индикаторной диаграммы

Индикаторная линия представляет собой кривую, выражающую зависимость расхода (дебита) от перепада давления (депрессии):

. (2.31)

При выполнении закона А. Дарси график этой зависимости представляет собой кривую линию, проходящую через начало координат.

Таблица 2.4 - Данные к построению индикаторной кривой

Q, м3/сут	∆pc, Мпа	Q, м3/сут	∆pc, МПа
0	0,00	160	2,45
20	0,3	180	2,77
40	0,63	200	3,08
60	0,92	220	3,4
80	1,24	240	3,7
100	1,55	260	4,01
120	1,85	280	4,32
140	2,16	300	4,62

Рисунок 2.5 – Индикаторная диаграмма