Определение потерь давления при подъёме нефти по нкт

Потери напора определяются по формуле:

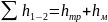, (2.19)

где 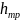– потери напора на трение, м;

– местные потери напора, м.

Потери энергии по длине обусловлены силами трения, возникающими при трении между жидкостью и твердыми стенками, а также между частицами от взаимного соприкосновения.

Местные сопротивления возникают при резких изменениях движения жидкости по величине и направлению в результате конструктивных особенностей трубы.

Поскольку изменений направления движения нефти по рассматриваемому участку насосно-компрессорных труб нет, то потерями напора в местных сопротивлениях можно пренебречь.

Для определения потерь напора на трение используется формула Дарси-Вейсбаха:

, (2.20)

которую можно записать в ином виде

, (2.21)

где λ – коэффициент гидравлического сопротивления;

l – длина участка трубы, м;

d – диаметр участка трубы, м;

υ – скорость в данном сечении, м/с.

Учитывая, что скорость потока можно определить как , где S– площадь поперечного сечения, выразим формулу (2.20) для определения потерь давления через расход:

. (2.22)

Следующим шагом будет определение значений коэффициента гидравлического сопротивления, для чего сначала необходимо определить число Рейнольдса – критерий, характеризующий характер течения.

Критерий Рейнольдса представляет собой безразмерную величину, значение которой не зависит от применяемой для её определения системы единиц измерения. Он является мерой отношения кинетической энергии жидкости к работе сил вязкого трения:

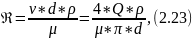
Движение в трубах всегда ламинарное, если Re ≤ 2300, тогда коэффициент гидравлического сопротивления рассчитывается по формуле Стокса:

При значении числа Re> 2300 движение жидкости турбулентное, тогда при определении коэффициента гидравлического сопротивления следует учитывать относительную шероховатость стенок трубы – Δ/d. Для значений чисел Рейнольдса, лежащих в интервале, когда , коэффициент гидравлического сопротивления рассчитывается по формуле Блазиуса:

Область со значениями чисел Рейнольдса, лежащих в интервале 2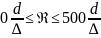 , принято называть областью шероховатых труб или областью смешанного трения. В этом пределе значений используется формула Альтшуля:

. (2.26)

При значении числа Рейнольдса, попадающего в интервал, когда , используется формула Шифринсона для квадратичной области сопротивления или вполне шероховатых труб:

, (2.27)

С учётом всех преобразований уравнение (2.18) примет вид:

Построение графика зависимости дебита от давления в нкт

Для построения графика зависимости дебита от давления в НКТ задаёмся различными значениями дебита от 0 до 300 м³/сут. с шагом 20 м³/сут.

Определим по формуле (2.28), выражающей общее условие работы фонтанного подъёмника значения давлений на забое скважины, согласно соответствующим значениям дебита.

График зависимости давления на входе в НКТ от дебита представляет собой кривую эффективности лифта, характеризующую пропускную способность НКТ при фиксированном устьевом давлении.

Таблица 2.2 – Значения для построения графика

Q, м3/с	υ, м/с	Re	λ	Δpтр, кПа	Рс, Мпа
0	0	0	0	0	18,927
0,00023	0,076	1295	0,05	4,35	18,932
0,00046	0,153	2607	0,044	15,5	18,943
0,00069	0,23	3919	0,04	31,86	18,96
0,00093	0,31	5282	0,037	53,55	18,98
0,00116	0,386	6577	0,0357	78,53	19
0,00139	0,463	7889	0,0353	112,99	19,04
0,00162	0,54	9202	0,034	149,3	19,075
0,00185	0,62	10565	0,0337	191,04	19,115
0,00208	0,69	11758	0,0333	238,76	19,167
0,00231	0,77	13121	0,0327	291,98	19,22
0,00255	0,85	14484	0,0321	349,27	19,274
0,00278	0,926	15779	0,0317	409,35	19,334
0,00301	1	17040	0,0313	471,37	19,398
0,00324	1,08	18403	0,0309	542,78	19,466
0,00347	1,156	19698	0,0306	615,82	19,54

Рисунок 2.2 - График зависимости пропускной способности НКТ от забойного давления