2. Расчетная часть

Одной из основных задач при эксплуатации скважины является задача расчётных дебита скважины соответствующего пропускной способности насосно-компрессорных труб (НКТ), что определяет устойчивую работу системы ″пласт – скважина″.

Совместная работа пласта и скважины (фонтанного подъемника) заключается в установлении общего забойного давления при условии обеспечения пластом такого дебита, который фонтанный подъемник будет в состоянии пропустить при данной глубине скважины, противодавлении на устье, диаметре колонны насосно-компрессорных труб и т.д.

2.1 Определение зависимости дебита от забойного давления при эксплуатации нефтяной залежи Вывод зависимости дебита от забойного давления

Расчёт дебита скважины базируется на уравнении притока жидкости из пласта в скважину, выраженного формулой Дюпюи в случае рассмотрения установившегося притока однородной несжимаемой жидкости в однородном недеформируемом пласте к гидродинамически совершенной скважине:

, (2.1)

где Q ‒ дебит скважины, м³/с;

k – коэффициент проницаемости пласта, м²;

µ ‒ коэффициент динамической вязкости жидкости, Па·с;

h ‒ мощность (толщина) пласта, м;

‒ радиус контура питания, м;

‒ радиус скважины, м;

‒ давление на контуре питания (пластовое давление), Па;

‒ давление на забое скважины, Па.

‒ приведенный радиус скважины.

Данную формулу можно записать, используя коэффициент продуктивности скважины, характеризующий её производительность, то есть дебит, приходящийся на единицу перепада давления (депрессии):

, (2.2)

где K ‒ коэффициент продуктивности скважины, м³/с·Па;

‒ депрессия, Па.

Тогда уравнение притока жидкости к забою скважины имеет вид:

(2.3)

решая, которое относительно давления на забое скважины получим:

. (2.4)

Приведенный радиус скважины можно рассчитать по формуле:

, (2.5)

где – радиус скважины,

– коэффициент несовершенства скважины по характеру скрытия.

Коэффициент несовершенства скважины по степени вскрытия находим по графику В. И. Щурова. Для этого необходимо:

1. Вычислить отношение :

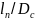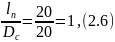
где 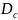– диаметр скважины.

2. Вычислить отношение :

3. Найти значение :

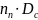4. По графику В. И. Щурова находим :

Рассчитываем приведенный радиус скважины:

Определение пластового давления

Для определения пластового давления необходимо рассмотреть распределение давления в затрубном пространстве.

Пространство между эксплуатационной колонной и насосно-компрессорными трубами в нижней части заполнено - неподвижной жидкостью, в верхней – газом. Соответственно, необходимо применить основное уравнение гидростатики и закон Паскаля.

Закон распределения давления в покоящемся газе задаётся в барометрической форме:

, (2.9)

где p_г– давление в покоящемся газе, Па;

–давление в затрубном пространстве до начала эксплуатации, Па;

– плотность газа при нормальных условиях, кг/м³;

–высота столба газа в затрубном пространстве до начала эксплуатации, м;

p_атм – атмосферное давление, Па.

Таким образом,

.

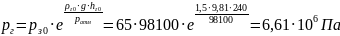Давление в покоящейся жидкости рассчитывается по формуле:

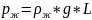, (2.10)

где – плотность жидкости,кг/м³;

L – глубина погружения НКТ, м.

, (2.11)

где H – глубина скважины, м.

Таким образом,

,

Па.

В случае если задвижка закрыта, т.е. притока флюида нет, то давление на забое скважины, будет равно пластовому давлению.

Пластовое давление определим согласно закону Паскаля, как сумму давления в покоящемся газе и давления в покоящейся жидкости:

. (2.12)

Таким образом,

.

Определение коэффициента продуктивности скважины

По условию задания эксплуатируется гидродинамически несовершенная скважина по степени вскрытия. Так как пласт по условию задания однородный кольцеобразной формы, то формула дебита скважины будет иметь вид:

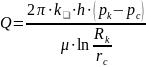, (2.13)

Найдем значение коэффициента продуктивности скважины:

м³/Па·с.