1.3.2. Статистичні міри інформації

Нам досить часто доводиться чути таку фразу: “Я отримав дуже мало інформації, оскільки знав, що буде сказано, ще до початку розмови”. Подібні висловлювання свідчать про те, що кількість інформації в деякому повідомленні зменшується, якщо одержувач знає заздалегідь або може вгадати якусь частину повідомлення, що передається. Це стає можливим, коли деякі повідомлення (із загальної кількості можливих) формуються джерелом частіше, порівняно з іншими. Оскільки кожному повідомленню, як правило, ставлять у відповідність деякий стан джерела, то в даній ситуації можна казати про наявність деяких “кращих” станів, у яких джерело повідомлення перебуває частіше.

У разі статистичного підходу отримання конкретного повідомлення та оцінку кількості інформації в ньому розглядають як результат деякого вибору серед можливих повідомлень.

Коли приходить повідомлення про події, що часто відбуваються, ймовірність появи яких p прямує до одиниці, таке повідомлення мало інформативне. Стільки ж мало інформативні в середньому повідомлення про події, ймовірність яких прямує до нуля, тобто майже неможливих подій, оскільки повідомлення про такі події надходять дуже рідко.

Утворення конкретного повідомлення можна представити як подію, що є результатом перебування джерела в одному з можливих станів. Оскільки джерело завжди знаходиться в одному зі станів, усі можливі повідомлення (події) складають ансамбль або повну групу. Ансамбль характеризується тим, що сума ймовірностей усіх повідомлень у ньому дорівнює одиниці, тобто

.

(1.54)

Наприклад, як події можна розглядати дискретні значення вимірюваної величини, стан елементів обладнання, розташування регулювальних органів тощо. Таблицю, що пов’язує події ансамблю та ймовірності їх появи, називають статистичною схемою ансамблю.

Прикладом може бути статистична схема джерела повідомлення, що використовує m елементів алфавіту (табл. 1.1)

Таблиця 1.1

Елементи алфавіту	x1	x2	x3	...	xi	...	xm
Ймовірності появи елементів	p1	p2	p3	...	pi	...	pm

У загальному випадку ймовірності не залишаються постійними, а можуть змінюватись за часом, у залежності від умов і т. д. У такому випадку статистичні характеристики стають змінними величинами.

Розглянемо повідомлення, що складаються з n елементів, кожен з яких є незалежним та вибирається з алфавіту, що містить m літер, з ймовірностями вибору елементів p₁, p₂,..., p_i,..., p_m відповідно. Уявімо, що в деяке повідомлення увійшло n₁ елементів x₁ алфавіту, n₂ елементів x₂ і т. д. Таке повідомлення характеризує табл. 1.2.

Таблиця 1.2

Елементи алфавіту	x1	x2	x3	...	xi	...	xm
Число елементів	n1	n2	n3	...	ni	...	nm
Ймовірності вибору елементів	p1	p2	p3	...	pi	...	pm

Ймовірність того, що в повідомлення увійдуть n_i елементів x_i дорівнює , а ймовірність утворення повідомлення з n₁, n₂,..., n_i,..., n_m відповідних елементів буде дорівнювати

.

(1.55)

За великої довжини n джерелом будуть формуватися типові повідомлення, в яких відносна частота появи окремих елементів x_i, тобто відношення числа даних елементів n_i до загального числа елементів у повідомленні прямує до ймовірності появи цих елементів, тобто

.

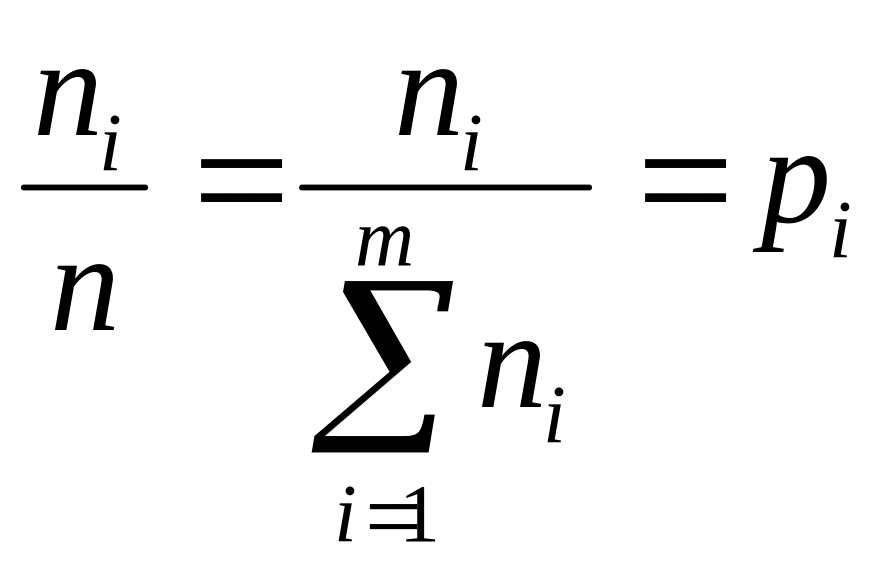(1.56)

Таким чином, у типове повідомлення достатньо великої довжини n, що виробляється джерелом з наведеною статистичною схемою, будуть входити n_i = p_in елементів виду x_i, а ймовірності появи типових повідомлень p будуть однакові [    ] і можуть бути знайдені з урахуванням виразів (1.55) та (1.56)

.

(1.57)

Оскільки сумарна ймовірність усіх типових повідомлень прямує до одиниці у разі збільшення довжини повідомлення, число типових повідомлень можна визначити за формулою

.

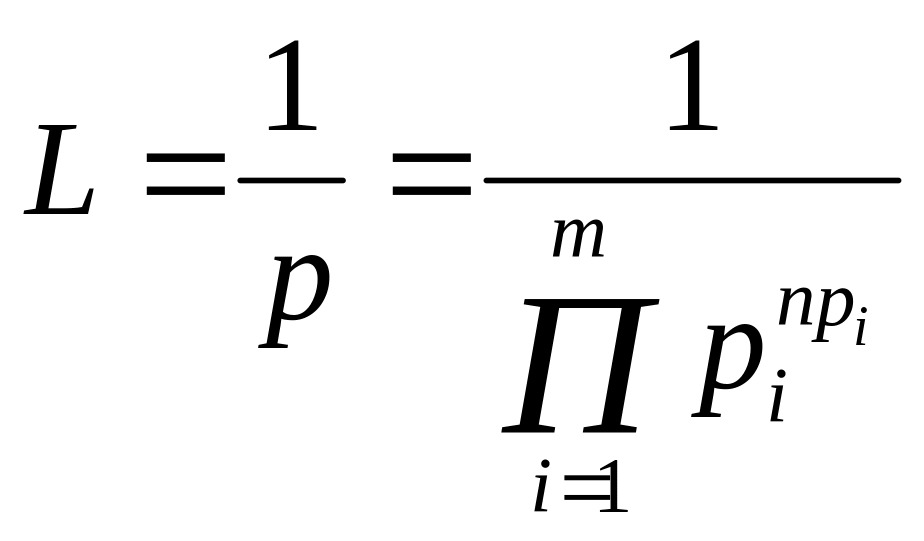(1.58)

Хоча число можливих повідомлень джерела mⁿ, джерело майже завжди буде виробляти тільки L типових повідомлень. Ясно, що оцінюючи інформаційні властивості джерела, слід враховувати саме цю частину можливих повідомлень, оскільки ймовірність появи інших повідомлень прямує до нуля [1-15].

Кількість інформації І в одному повідомленні

І = .

(1.59)

Кількість інформації в повідомленні залежить не тільки від кількості елементів, але й від його складу, тобто ймовірності елементів, що входять до повідомлення¹⁾.

Кількість інформації, яка приходиться на один елемент повідомлення, називають питомою інформативністю або ентропією. Ентропія характеризує джерело повідомлення із заданим алфавітом та є мірою невизначеності, яка є в ансамблі повідомлення цього джерела. Чим більша ентропія, тим більше інформації несе повідомлення джерела, тим більша невизначеність усувається у разі отримання повідомлення. Звичайно ентропію позначають літерою Н та визначають виразом

.

(1.60)

Кількість інформації та ентропія є логарифмічними мірами, їх вимірюють у одних і тих самих одиницях. Основа логарифму визначає одиницю вимірювання кількості інформації та ентропії. Двійкова одиниця відповідає основі логарифму, що дорівнює двом, та називається бітом. 1 біт – це кількість інформації в повідомленні про одне з двох рівноймовірних результатів одного досліду. Використовують також натуральні та десяткові логарифми. У цих випадках кількість інформації виражають у натуральних та десяткових одиницях відповідно. Аналогічні одиниці використовують для оцінки кількості інформації за допомогою адитивної міри Хартлі (1.51).