1.2. Повідомлення та відповідні їм сигнали

Д жерела та форми повідомлення та відповідні їм сигнали можна поділити на дискретні та неперервні.

Дискретними називають повідомлення, що складаються з окремих елементів (символів, букв, імпульсів), які приймають скінченну кількість різних значень. Прикладами дискретних повідомлень є команди в системах керування, вихідна інформація ЕОМ у вигляді кодових груп або масивів чисел, телеграфні повідомлення. Такі повідомлення складаються зі скінченної кількості елементів, що слідують один за одним у деякій послідовності. Набір елементів, з яких складаються повідомлення, як правило, називають алфавітом.

Неперервними називають такі повідомлення, я кі можуть приймати в деяких межах будь-які значення та являються неперервними функціями часу (рис. 1.3).

Прикладами таких повідомлень і відповідних їм сигналів є телефонні повідомлення, сигнали телеметрії, відеосигнали, що відображають розподіл яскравості в телевізійному зображенні.

У реальних умовах згадані відмінності неперервних та дискретних повідомлень можуть бути непринциповими. Шляхом дискретизації (за часом) та квантування (за рівнем) можна неперервне повідомлення з допустимим степенем наближення замінити дискретним (рис.1.4.).

З інформаційної точки зору сигнали можна розділити на детерміновані та випадкові.

Детермінованим називають сигнал, математичним представленням якого є деяка задана функція часу. Це означає, що детермінований сигнал відповідає відомому повідомленню і тому його миттєве значення в будь-який момент часу можна передбачити досить точно.

Прикладами детермінованих сигналів є: гармонічний сигнал з відомими амплітудою, частотою та фазою; імпульси або послідовність імпульсів з відомими формою, амплітудою та розташуванням у часі.

Випадковим називають сигнал, математичним представленням якого є випадкова функція часу. Це означає, що точні значення такого сигналу невідомі й можуть бути передбачені лише приблизно, з деякою ймовірністю.

Прикладами випадкових сигналів є мовні сигнали, сигнали електрокардіограм, сигнали на вході радіолокаційних приймачів тощо.

З точки зору теорії інформації детерміновані сигнали інформації не несуть, тому будь-який сигнал, який несе інформацію, слід розглядати як випадковий.

Реальні сигнали поєднують властивості як детермінованих, так і випадкових сигналів.

В ластивості випадкових сигналів розглядають, використовуючи теорію випадкових процесів, у відповідності з якою реальний сигнал являє собою одну з можливих реалізацій випадкового процесу. Сукупність реалізацій випадкового процесу називають ансамблем, який є множиною реалізацій випадкового процесу {x(t)} (рис. 1.5).

Характеристики випадкового процесу визначають у середньому не за одною, а за сукупністю великої кількості реалізацій випадкового процесу. Основними характеристиками є закони розподілу значень випадкового процесу.

Одновимірний інтегральний закон розподілу характеризується функцією розподілу F₁, що визначають для часового перетину, який відповідає моменту t₁

F1(x1,t1) = P[x(t1) ≤ x1],

(1.1)

де P[x(t₁) ≤ x₁] – ймовірність того, що в момент t₁ значення випадкового процесу знаходяться в межах

x_min < x < x₁,

де x_min та x_max – межі можливих значень випадкового процесу.

Функція F₁(x₁,t₁) може бути знайдена з виразу

,

(1.2)

де p₁(x,t) – одновимірна щільність імовірності випадкового процесу для моменту часу t₁.

Одновимірна щільність імовірності, так само як і одновимірний закон розподілу, недостатні для повного опису випадкового процесу, оскільки характеризують його лише в окремі моменти часу.

Повніше випадковий процес характеризують двовимірні, тривимірні і т. д. закони розподілу, що дають змогу враховувати зв’язок значень випадкового процесу в моменти часу (t₁, t₂), (t₁, t₂, t₃), (t₁, t₂…t_n), що вибирають довільно. Найбільш повною характеристикою випадкового процесу є n-вимірний закон розподілу. Багатовимірні закони характеризуються багатовимірними функціями розподілу та багатовимірною щільністю ймовірності.

Зокрема, двовимірний закон описують функцією розподілу

(1.3)

та характеризують двовимірною щільністю ймовірності P₂(x₁,t₁; x₂,t₂).

Вичерпною характеристикою випадкового процесу є n-вимірний закон розподілу, що описує розподіл значень x(t) для n довільно вибраних моментів часу

.

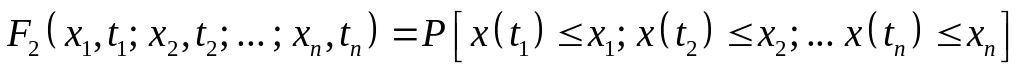(1.4)

Вважають, що випадковий процес X(t) заданий, якщо його n-вимірний розподіл відомий для будь-якої кількості n довільно вибраних моментів часу t₁, t₂, ... t_n.

Коли значення випадкового процесу для будь-яких t незалежні, n-вимірну щільність ймовірності p_n(x₁,t₁; x₂,t₂;...; x_n,t_n) можна записати у вигляді добутку одновимірних щільностей імовірності

pn(x1,t1; x2,t2;...; xn,tn)=p1(x1,t1)·p1(x2,t2)...p1(xn,tn).

(1.5)

Поряд із законами розподілу випадкові процеси характеризують рядом параметрів, які отримують у загальному випадку шляхом усереднення за множиною реалізацій (усереднення за множиною реалізацій позначено прямою рискою над функцією в (1.6) і далі).

Середнє значення – математичне очікування випадкового процесу

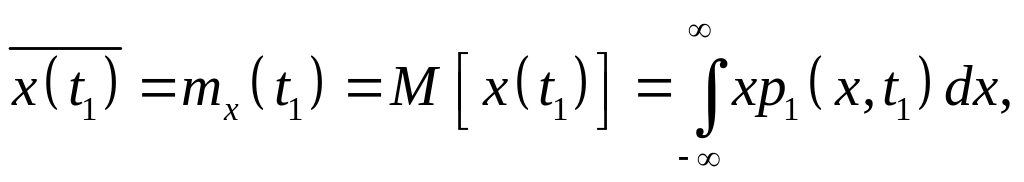
(1.6)

де М – символ операції обчислення математичного очікування.

Середнє значення квадрата випадкового процесу

(1.7)

Дисперсія – математичне очікування квадрата відхилення випадкового процесу

(1.8)

У даному випадку – середнє квадратичне відхилення.

Дисперсія – це міра відхилення випадкового процесу від середнього значення. Якщо , дисперсія дорівнює середньому значенню квадрата випадкового процесу. Наведені параметри характеризують випадковий процес у визначений момент часу t₁. Випадковий процес X(t) – m_x(t) називають центрованим.

Статистичний зв’язок між значеннями випадкового процесу оцінюють функцією кореляції

,

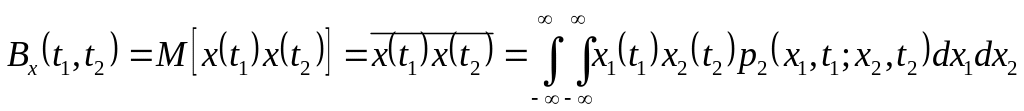(1.9)

що являє собою статистично усереднений добуток значень випадкового процесу, які взяті в моменти часу t₁ та t₂.

Статистичний зв’язок між двома випадковими процесами описують взаємною кореляційною функцією

,

(1.10)

де p₂(x₁,t₁; y₂,t₂) – двовимірна взаємна щільність імовірності випадкових процесів X(t) та Y(t).

Якщо випадкові процеси X(t) та Y(t) статистично незалежні, то p₂(x₁,t₁; y₂,t₂) = p₁(x₁,t₁)p₁(y₂,t₂) і тоді функція взаємної кореляції може бути знайдена як добуток середніх значень випадкових процесів, тобто .

Відмітимо ще раз, що наведені параметри визначають шляхом статистичного усереднення за множиною реалізацій. Можливе визначення цих параметрів і шляхом усереднення за часом на деякому часовому інтервалі, який принципово можна розширити до нескінченності. Наприклад, середнє за часом (позначають хвилястою лінією зверху)

,

(1.11)

а середнє значення квадрата випадкового процесу

і т. д.

(1.12)

У загальному випадку середні за ансамблем реалізації та середні за часом не рівні, оскільки середні за ансамблем є функціями моментів часу t₁ або t₁, t₂ (кореляційна функція).

Наведені співвідношення надані для неперервного випадкового процесу. Якщо ж випадковий процес є дискретним і є ансамблем випадкових величин x_i, то можна записати співвідношення, аналогічні (1.6) – (1.9):

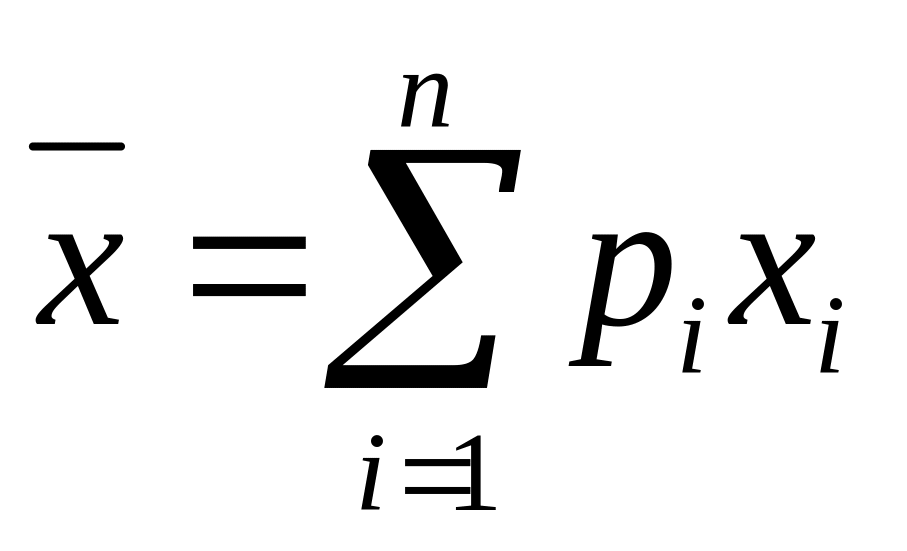,	(1.13)
,	(1.14)
,	(1.15)
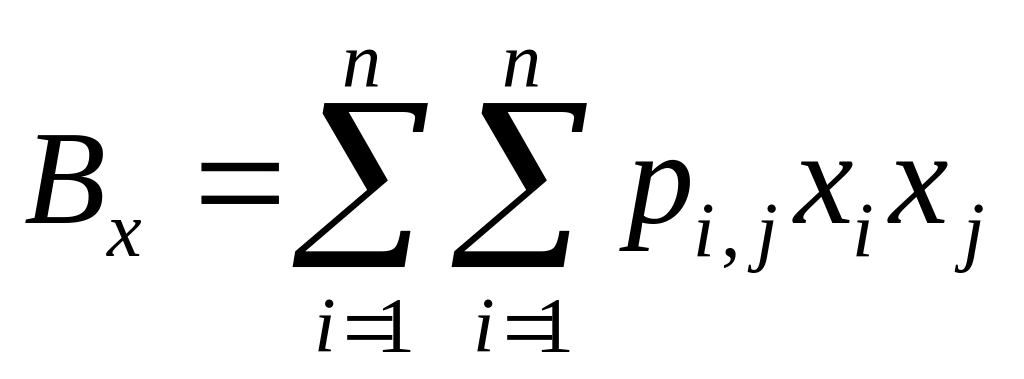,	(1.16)

де p_i – апріорна ймовірність випадкової величини x_i; p_i,j – сукупна апріорна ймовірність величин x_i та x_j; n – кількість значень випадкової величини x.