1.4.3. Принцип дискретизації Желєзнова

Н. А. Желєзновим було розв’язано задачу визначення максимального інтервалу між відліками випадкового повідомлення [1-8]. У моделі, що використовувалась, повідомлення характеризуються такими параметрами: скінченною тривалістю T_с, спектром, відмінним від нуля на всій частотній осі, тобто S(ω) ≠ 0, якщо –∞ ≤ ω ≤ ∞.

Вводять допущення обмеженості інтервалу кореляції (тобто вважається, що функція кореляції дорівнює нулю поза інтервалом τ₀) та малості інтервалу кореляції порівняно з тривалістю повідомлення (T_с >> τ₀). Розглядають повідомлення, які є стаціонарними та нестаціонарними функціями часу. Введені допущення не вступають у протиріччя з природою реальних повідомлень. Оскільки внаслідок скінченної тривалості їх значення в будь-який момент залежать тільки від деякого відрізку минулого обмеженої тривалості. Тому інтервал кореляції реальних повідомлень є обмеженою величиною.

Н. А. Желєзновим доведено, що такі повідомлення можна відновити за допомогою системи лінійного прогнозування із середньоквадратичною помилкою, яка скільки завгодно мало відрізняється від нуля, тільки на проміжку часу, що дорівнює інтервалу кореляції τ₀. Таким чином, згідно [1-8] дискретизацію слід проводити з інтервалом, що не перевищує τ₀, оскільки лише в цьому випадку можливе безпомилкове відновлення початкового повідомлення.

Сформульована Н. А. Желєзновим теорема, згідно якої “ неперервні квазістаціонарні сигнали з необмеженим спектром можна передавати за допомогою чисел, що слідують одне за одним через проміжок часу ∆t, з достовірністю, скільки завгодно близькій до граничної вірності δ², якщо проміжок ∆t не перевищує інтервал кореляції τ₀, а тривалість сигналу Т_с набагато більша за інтервал кореляції τ₀”, є узагальненням теореми В. А. Котєльнікова.

Неперервна функція x(t) представлена у вигляді ряду

,

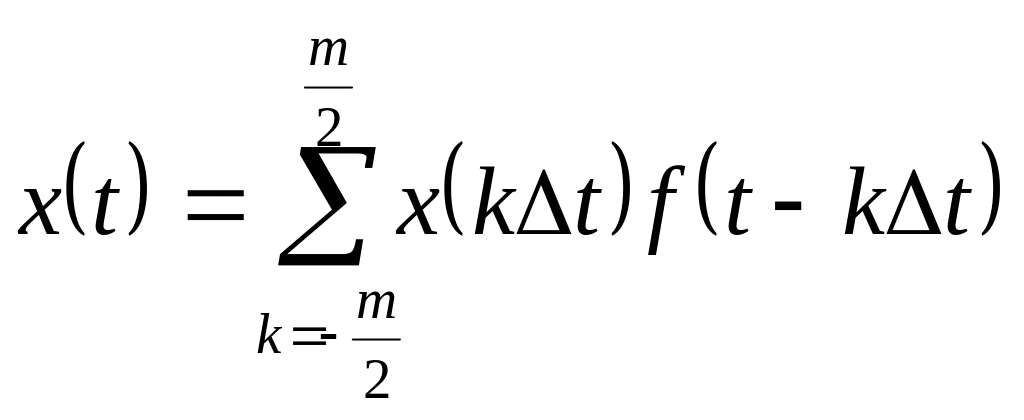(1.138)

в якому вибір базисної функції f(t – k∆t) залежить від характеру кореляційної функції B_x(τ). Для випадку, коли

середньоквадратична похибка визначиться виразом

,

(1.139)

де τ₀ – інтервал кореляції.

Кількість некорельованих відліків m дорівнюватиме

.

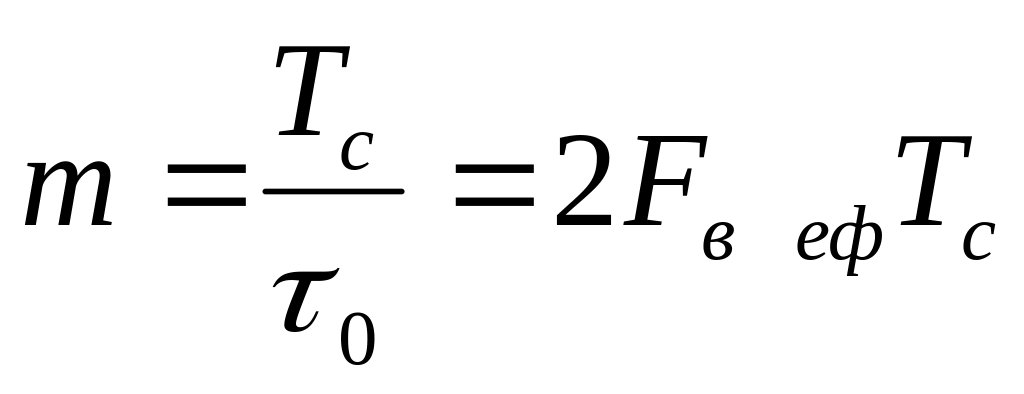(1.140)

Визначення інтервалу кореляції здійснюють за формулами (1.25), (1.26), (1.46).

Для нестаціонарних функції використовують поняття поточного інтервалу кореляції, який є функцією часу τ₀ = τ₀(t). У цьому випадку відлікові значення неперервного повідомлення будуть розташовані на осі часу нерівномірно.

1.4.4. Дискретизація неперервних повідомлень з використанням критерію найбільшого відхилення

Вибір інтервалу дискретизації з використанням даного критерію відбувається з припущенням, що початкове повідомлення відновлюється за допомогою поліному степеня n. На деякому відрізку часу [t₀, t_n] для рівновіддалених відліків повідомлення x΄(t) може бути представлено виразом

.

(1.141)

Вводячи скорочений запис, отримаємо

.

(1.142)

Для відновлення функції x(t) за допомогою поліному степеня n необхідно мати n + 1 відліків.

Похибка відновлення початкового повідомлення в цьому випадку визначиться залишковим членом

,

(1.143)

де x⁽ⁿ⁺¹⁾(ξ) – значення (n + 1)-ої похідної повідомлення x(t), взятої в деякій точці ξ, яка лежить усередині інтервалу t_n – t₀. Оскільки положення точки ξ невідоме, для оцінки використовують модуль максимуму похідної М_n+1 на заданому інтервалі. Тоді

.

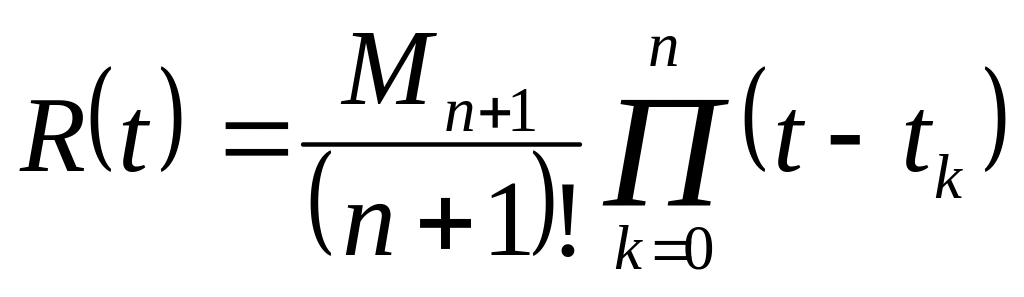(1.144)

Вводячи обмеження

,

(1.145)

де ε₀ – припустима похибка дискретизації за часом, можна знайти інтервал дискретизації t або довжину інтервалу t_n – t₀, на якому необхідно визначити n + 1 відлікових значень неперервного повідомлення. За цих умов інтервал t_n – t₀ є деякою функцією похибки ε₀, степеня відновлюючого поліному і т. д.

Інтерес представляє визначення інтервалу дискретизації у разі використання відновлювальних поліномів нульового та першого степеню.

Нульовому степеню відновлювального поліному відповідає ступінчаста апроксимація неперервного повідомлення. У цьому випадку (1.145) прийме вигляд

,

звідки

.

(1.146)

Якщо n = 1 (лінійна апроксимація), залишковий член визначиться як

.

Максимізуючи добуток 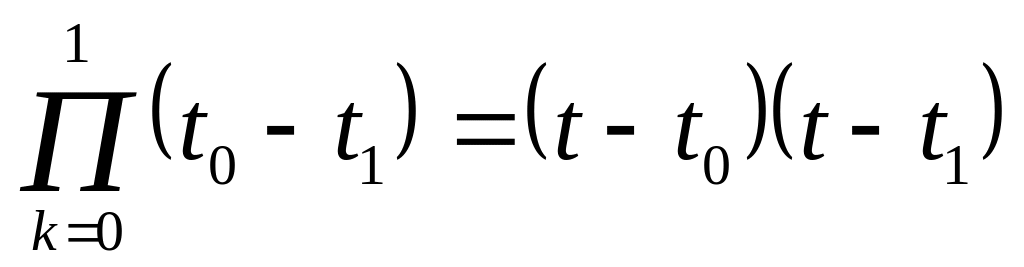, отримаємо , звідки

.

(1.147)

Відновлення неперервного повідомлення з використанням поліномів нульового та першого степеня представлено на рис. 1.18.

Значення кроку дискретизації для поліномів вищих степенів наведено в табл. 1.5.

Таблиця 1.5

Степінь поліному	0	1	2	3	4
Крок дискретизації

С лід відмітити, що деяких видів повідомлень частота дискретизації, визначена вказаним методом, значно менша за частоту, знайдену за теоремою Котєльнікова. Наприклад, для відновлення повідомлення, описаного експоненціальною функцією , якщо τ = 1 с, з похибкою 0,5%, за теоремою Котєльнікова потрібна частота дискретизації більша 8 кГц, тоді як за критерієм найбільшого відхилення для n = 1 частота дискретизації становить 5 Гц. Якщо похибка становить 0,05%, значення частоти будуть відповідно більшими: 700кГц та 15,9 Гц. Різниця, обумовлена використанням різних методів відновлення повідомлення, є досить суттєвою.

Розглянуті способи не вичерпують усіх можливих способів відновлення неперервних повідомлень на основі їх дискретних значень. Для цієї цілі можуть використовуватись різні фільтри, характеристики яких суттєво впливають на вибір частоти дискретизації. Проте основними даними і в цьому випадку є ширина спектра повідомлення та припустима похибка відновлення неперервного повідомлення. Значення частоти дискретизації у разі використання деяких видів фільтрів (фільтр Батерворта, оптимальний фільтр, RC-фільтр) можна знайти в монографії [ 1-13].