
- •Содержание
- •Введение
- •Перечень практических занятий по учебной дисциплине «Математика»
- •Методические указания к практическому занятию №1
- •I вариант
- •II вариант
- •Методические указания к практическому занятию №2
- •Методические указания к практическому занятию №3
- •I вариант
- •II вариант
- •Методические указания к практическому занятию №4
- •I вариант II вариант
- •Методические указания к практическому занятию №5
- •Методические указания к практическому занятию №7
- •1. Справедливы соотношения:
- •Методические указания к практическому занятию №8
- •Методические указания к практическому занятию №9
- •Методические указания к практическому занятию №10
- •Методические указания к практическому занятию №11
- •Методические указания к практическому занятию №12
- •1. Перпендикулярность прямой и плоскости.
- •2. Признак перпендикулярности прямой и плоскости.
- •3. Теоремы о перпендикулярности прямой и плоскости.
- •4. Расстояние от точки до плоскости.
- •Методические указания к практическому занятию №13
- •Методические указания к практическому занятию №14
- •Методические указания к практическому занятию №15
- •I вариант
- •II вариант
- •Методические указания к практическому занятию №16
- •1. Возрастание и убывание функции
- •3.Схема исследования функции и построения ее графика
I вариант II вариант
1. Упростите выражение:
а) tgα ctgα – cos2α а) sin2α – ctgα tgα
б)
![]() б)
б)
![]()
2. По заданному значению одного из выражений найдите значения трех остальных:
sinα
=
![]() ,
< α < π cosα
= -
,
< α < π cosα
= -![]() ,
π < α
<
,
π < α
<
3. Докажите тождество:
![]() tg2α
– ctg2α
=
tg2α
– ctg2α
=
![]()
Контрольные вопросы
1. Запишите формулы суммы и разности аргументов.
2. Запишите формулы преобразования суммы в произведение.
3. Запишите формулы двойного аргумента.
4. Запишите формулы преобразования произведения в сумму.
Задание на дом
[1] с. 157-159, 160-164, №2.182; 2.1
Методические указания к практическому занятию №5
Тема: Свойства и графики тригонометрических функций
Цель: выполнять задания на построение и преобразование графиков тригонометрических функций, применять их свойства при решении задач.
Оснащение: таблица значений тригонометрических функций, модель «Тригонометрический круг», ТБ инструкция №48.
Литература: Алгебра. 10 кл Е.П. Кузнецова Минск “Народная асвета” 2008
Справочный материал
Функция y=sin x.
Рассмотрим функцию синус, заданную формулой y=sin x, с областью определения – множеством R.

Теорема (о свойствах функции y = sinx).
Область определения функции y = sinx — множество R.
Область (множество) значений функции y = sinx — промежуток [-1; 1].
Функция y = sinx периодическая с периодом
 .
.Наименьшее значение у = -1 функция y-sinx принимает в точках
 Наибольшее значение у
= 1 — в точках
Наибольшее значение у
= 1 — в точках
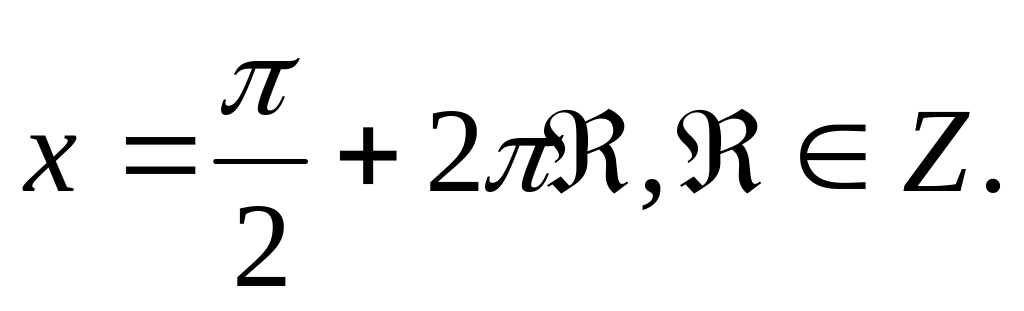
Нулями функции
 являются
значения аргумента
являются
значения аргумента
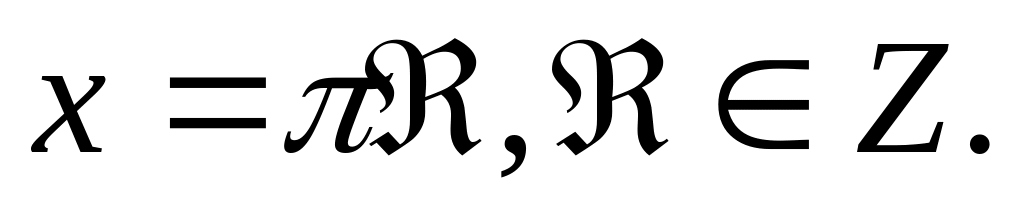
Функция y = sinx принимает отрицательные значения на каждом из промежутков (
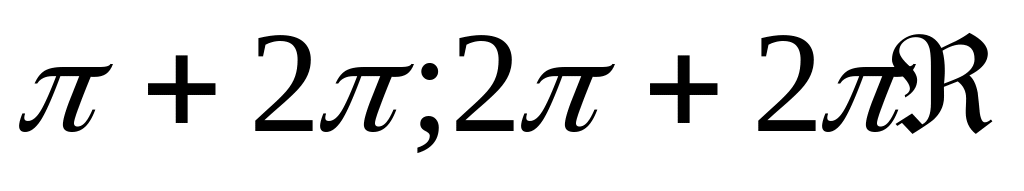 ),
), и
положительные значения на каждом из
промежутков
и
положительные значения на каждом из
промежутков
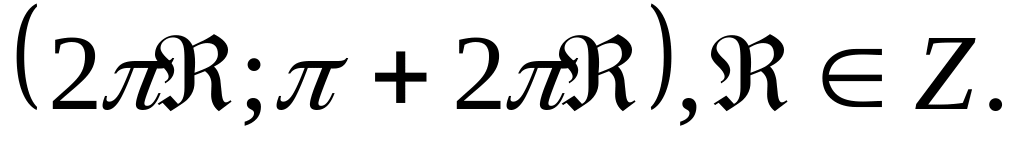
Функция y = sinx нечетная.
Функция y = sinx возрастает на каждом из промежутков
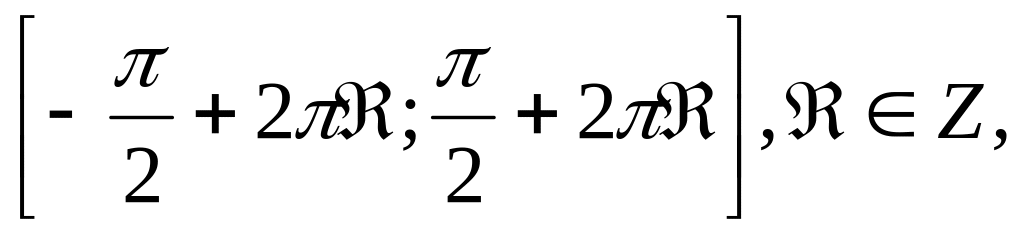 и
убывает на каждом из промежутков
и
убывает на каждом из промежутков
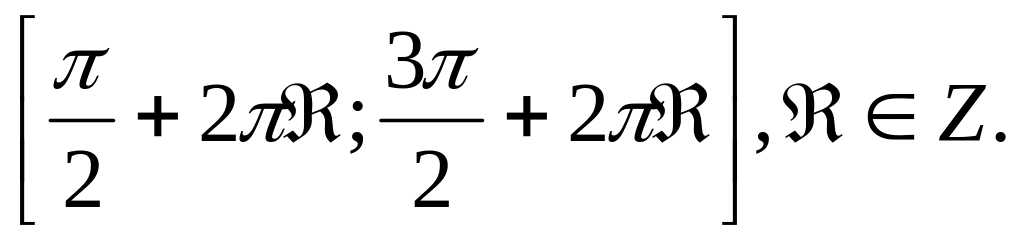
Пример 1. Сравнить значения выражений sin 7, sin 1, sin 4.
Решение. Имеем
![]() так
как 0,72 и 1 принадлежат промежутку
так
как 0,72 и 1 принадлежат промежутку
![]() а
на этом промежутке функция y=sin
x
возрастает и её значения неотрицательны.
а
на этом промежутке функция y=sin
x
возрастает и её значения неотрицательны.
Так как угол, радианная мера которого равна 4, оканчивается в III четверти, то sin 4<0.
Ответ: sin 4<sin 7<sin 1.
Функция y=cos x.
Рассмотрим функцию косинус, заданную формулой y=cos x, с областью определения – множеством R.

Теорема (о свойствах функции y=cos x).
Область определения функции y=cos x – множество R.
Область (множество) значений функции y=cos x – промежуток [-1;1].
Функция y=cos x периодическая с периодом .
Наименьшее значение y=-1 функция y=cos x принимает в точках
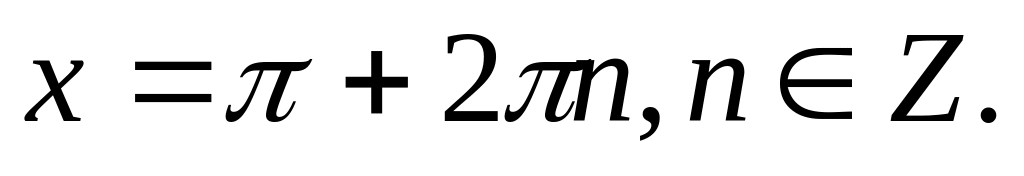 Наибольшее значение y=1
функция y=cos
x
принимает в точках
Наибольшее значение y=1
функция y=cos
x
принимает в точках

Нулями функции y=cos x являются значения аргумента

Функция y=cos x принимает отрицательные значения на каждом из промежутков
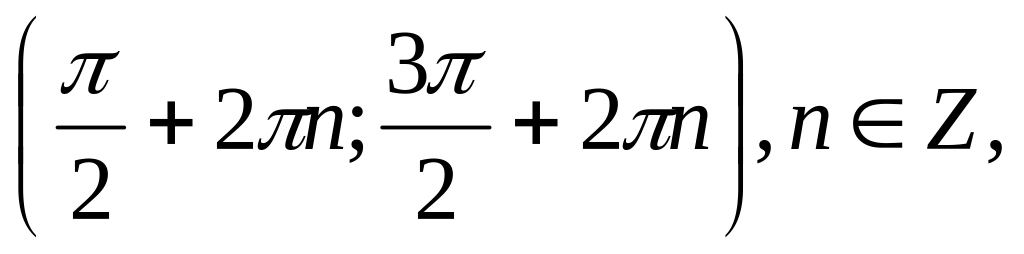 и
положительные значения на каждом из
промежутков
и
положительные значения на каждом из
промежутков

Функция y=cos x чётная.
Функция y=cos x убывает на каждом из промежутков
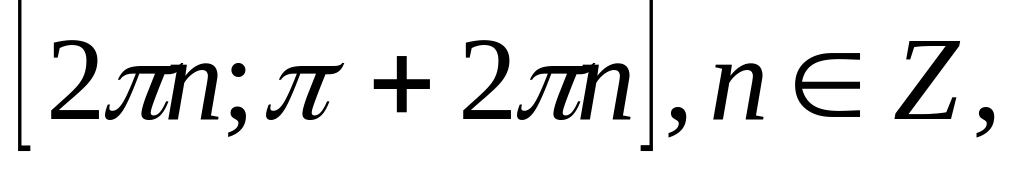 и возрастает на каждом из промежутков
и возрастает на каждом из промежутков
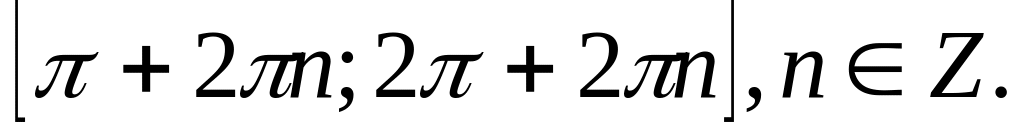
Пример 1.
Функция задана формулой
![]() на множестве D.
Является ли эта функция четной, если:
на множестве D.
Является ли эта функция четной, если:
а)
![]() б) D=Z?
б) D=Z?
Решение. а) Функция
не является чётной, так как промежуток
D
– ее область определения – несимметричен
относительно начала координат:
![]()
б) Функция четная,
так как ее область определения D=Z
– множество,
симметричное относительно нуля, и для
любого
![]() имеем
имеем
![]()
Функция y=tg x
Рассмотрим функцию
тангенс, заданную формулой y=tg
x,
с область определения – множеством
действительных чисел
![]()

Теорема (о свойствах функции y=tg x).
Область определения функции y=tg x – множество действительных чисел
Область (множество) значений функции y=tg x – все действительные числа, т.е.множество R.
Функция y=tg x периодическая с периодом

Наибольшего и наименьшего значений функция y=tg x не имеет.
Нулями функции y=tg x являются значения аргумента
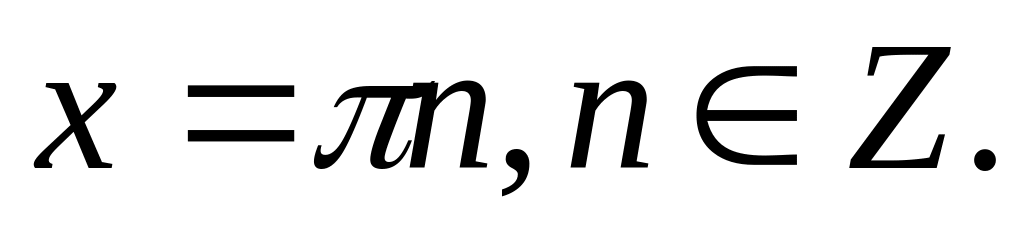
Функция y=tg x принимает отрицательные значения на каждом из промежутков
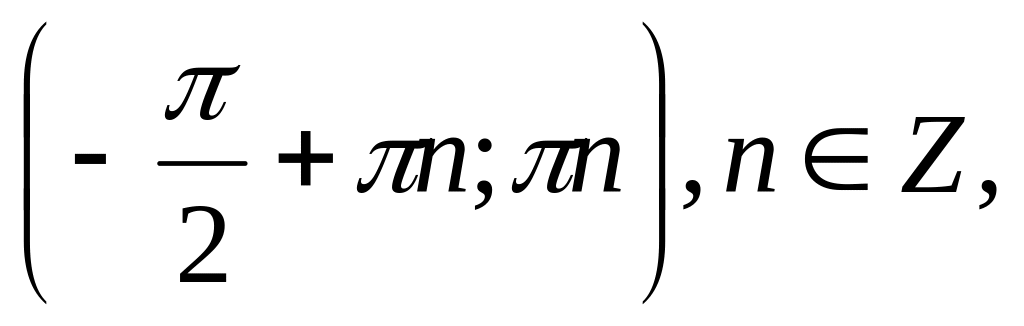 и
положительные значения на каждом из
промежутков
и
положительные значения на каждом из
промежутков
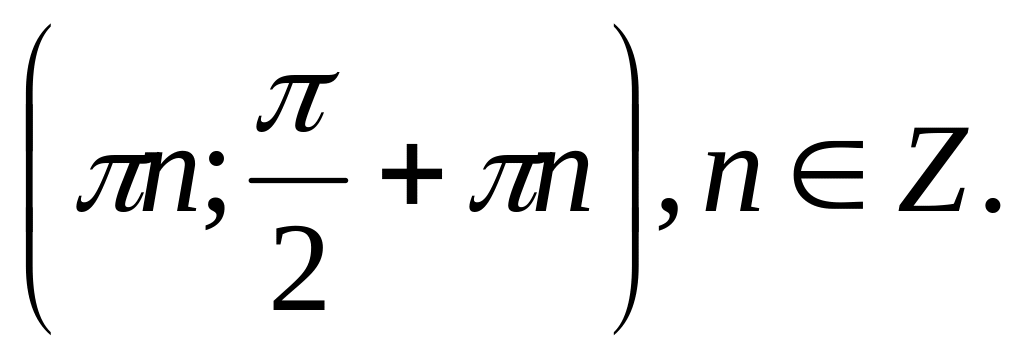
Функция y=tg x нечетная.
Функция y=tg x возрастает на каждом из промежутков

Функция y=ctg x.
Рассмотрим функцию
котангенс, заданную формулой y=ctg
x,
с областью определения – множеством
действительных чисел
![]()

Теорема (о свойствах функции y=ctg x).
Область определения функции y=ctg x – множество действительных чисел
Область (множество) значений функции y=ctg x – все действительные числа, т.е. множество R.
Функция y=ctg x периодическая с периодом
Наибольшего и наименьшего значений функция y=ctg x не имеет.
Нулями функции y=ctg x являются значения аргумента
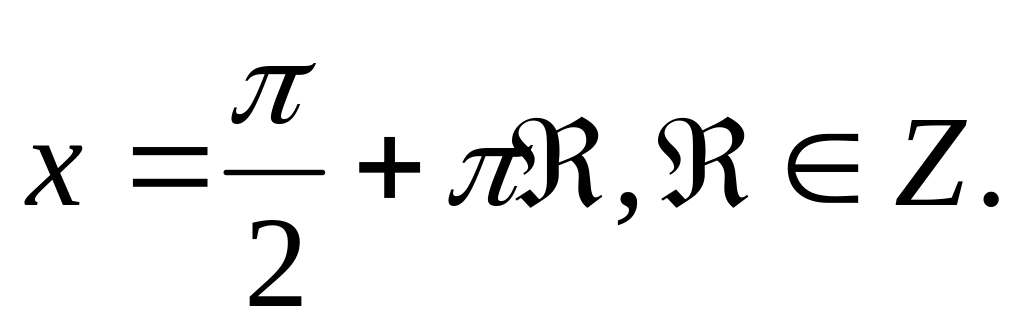
Функция y=ctg x принимает отрицательные значения на каждом из промежутков
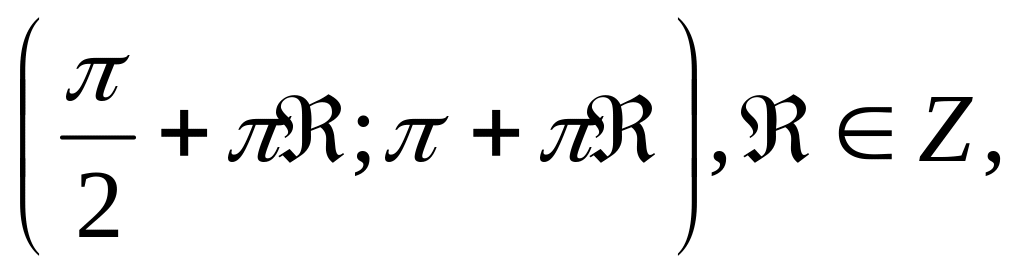 и
положительные значения на каждом из
промежутков
и
положительные значения на каждом из
промежутков
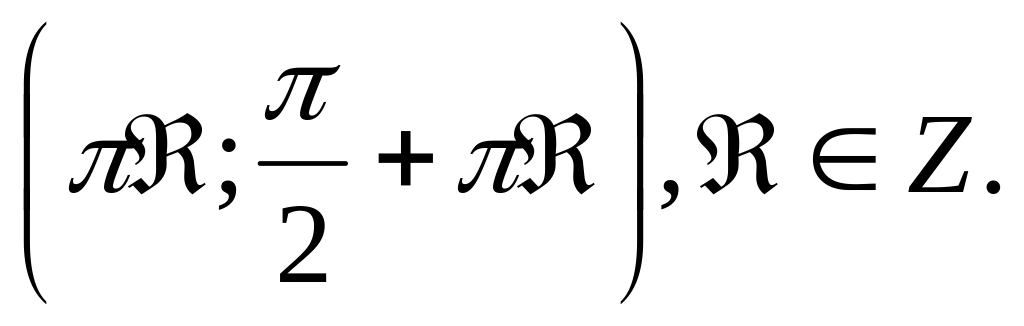
Функция y=ctg x нечетная.
Функция y=ctg x убывает на каждом из промежутков



Упражнения:
1.Среди перечисленных функций укажите тригонометрические функции:
а) y =-5 – tg x; б) y = 2ctg2 x + sin x;
в) г) у=5+5х2
2.Какими из перечисленных свойств обладает функция y = ctg x:
а) нечетная; б) периодическая; в) D(х) =R; г) Е(у) = [-1; 1]?
4.Постройте график функций у=sin 2х и укажите наибольшее и наименьшее значения функции.
5. Определите период функции:
а) f(x) = sin2 x – cos2 x; б) f(x) = 2sin 2x cos 2x.
Самостоятельная работа
I вариант
1.Среди перечисленных функций укажите тригонометрические функции:
а) у = 2cos 2x +5; б) у=сtg2x + sin3 x;
2.Какими из перечисленных свойств обладает функция y = sin x:
а) четная; б) непериодическая; в) D(х) =R; г) Е(у) = [-3; 4]?
§.
4.Постройте график функций у =2 cos х и укажите наибольшее и наименьшее значения функции.
5. Определите период функции:
а) f(x) = cos2 x – sin2 x; б) f(x) = 2sin 3x cos 3x.
II вариант
1.Среди перечисленных функций укажите тригонометрические функции:
а) у = sin x + 7; б) у= 2 cos 2 x + 3 tg2x;
§.
2.Какими из перечисленных свойств обладает функция y = cos x:
а) нечетная; б) периодическая; в) D(х) =R; г) Е(у) = [-3; 4]?
4.Постройте график функции b у =0,5 sin х и укажите наибольшее и наименьшее значения функции.
5. Определите период функции:
Контрольные вопросы:
Укажите наибольшее (наименьшее) значение функции y=sin x.
Укажите промежутки убывания (возрастания) функции y=cos x.
Чему равен наименьший положительный период функции y=tg x?
Назовите промежутки знакопостоянства функции y=ctg x.
Задание на дом
[1] с. 180-186, 189-194, 197-201, 204-208, №3.27; 3.61
Методические указания к практическому занятию №6
Тема: Решение простейших тригонометрических уравнений
Цель: решать простейшие линейные и квадратные уравнения относительно тригонометрических функций.
Оснащение: таблица значений тригонометрических функций, модель «Тригонометрический круг», ТБ инструкция №48.
Литература: Алгебра. 10 кл Е.П. Кузнецова Минск “Народная асвета” 2008
Справочный материал
1. Определение обратных тригонометрических функций и их простейшие свойства
Определения:
1) α = arc sinα sin α = a
-µ §
2) α = arc cosα cos α = a
0 ≤ х ≤ π
3) α = arc tgα tg α = a
-![]()
α = arc ctgα ctg α = a
0 < α < π
Свойства:
arc sin (-x) = - arc sin x
arc tg (-x) = - arc tg x
arc cos (-x) = π – arc cos x
arc ctg (-x) = π – atr ctg x
2. Простейшие тригонометрические уравнения
(n
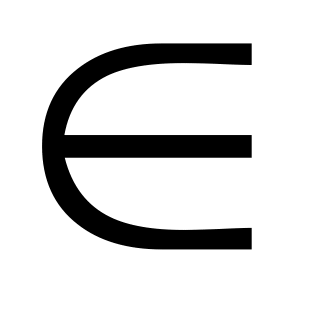 z)
z)
sin x = a x = (-1)n arc sin a + πn
![]()
2) cos x = a x = ± arc cos a + 2πn
tg x =
a
![]() x = arc tg a + πn
x = arc tg a + πn
ctg x = a x = arc ctg a +πn
а) sin x = 0 x = πn, д) cos x = 0 x = + πn,
б) tg x = 0 x = πn е) ctg x = 0 x = + πn,
в) sin x = 1 x = + 2πn, ж) sin x = -1 x = - + 2πn,
г) cos x = 1 x = 2πn, з) cos x = -1 π + 2πn
Упражнения
1.Корнем уравнения
cos
x
=1 является
число: а) π; б)
![]() ; в) 2π; г) 1.
; в) 2π; г) 1.
2.Решите уравнения:
а) tg x = 1;
![]()
3.Найдите множество корней уравнения:
![]()
![]()
![]()
![]()
Cамостоятельная работа
Вариант 1
1.Корнем уравнения cos x = - 1 является число: а) π; б) ; в) 2,5π; г) 1.
2.Решите уравнения:
![]()
3.Найдите множество корней уравнения:
![]()
![]()
![]()
Вариант 2
1.Корнем уравнения sin x = 0 является число: а) π; б) ; в) 2,5π; г) 1.
2.Решите уравнения:
![]()
3.Найдите множество корней уравнения:
![]()
![]()
![]()
Контрольные вопросы
1. Как называется и обозначается функция, обратная функции синуса?
2. Дать определение арксинуса и числа а.
3. Формула решения уравнения вида sin х = а.
4. Как называется и обозначается функция, обратная функции косинуса?
5. Дать определение арккосинуса числа а.
6. Формула решения уравнения вида cos х = а.
7. Как называется и обозначается функция, обратная функции тангенса?
8. Определение арктангенса числа а.
9. Формула решения уравнения вида tg х = а.
Задание на дом
[1] с. 211-216, 219-222, №3.102; 3.116
