Методические указания к практическому занятию №14
Тема: Углы между прямыми и плоскостями.
Цель: Решать задания на нахождение углов между геометрическими объектами в пространстве.
Оснащение: Модель «Теорема о трех перпендикулярах». ТБ инструкция №48.
Литература: Геометрия. 10 кл. В.В. Шлыков Минск «Народная асвета» 2008
Справочный материал
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые, параллельны данным скрещивающимся прямым.
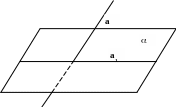
Пусть плоскость, а – пересекающая её прямая, не перпендикулярная плоскости . Основание перпендикуляров, опущенных из точек прямой а на плоскость , лежат на прямой а1. Эти прямая называется проекцией прямой а на плоскость . Углом между прямой и плоскостью называется угол между этой прямой и её проекцией на плоскость.
Упражнения:
Вершины A и D параллелограмма ABCD лежат в плоскости . Докажите, что прямые BA и CD образуют с плоскостью равные углы.
Прямая МА проходит через точку А плоскости и образует с этой плоскостью угол 0 90°. Докажите, что 0 является наименьшим из всех углов, которые прямая МА образует с прямыми, проведёнными в плоскости через точку А.
Наклонная АМ, проведённая из точки А к данной плоскости, равна d. Чему равна проекция этой наклонной на плоскость, если угол между прямой АМ и данной плоскостью равен: а) 45°; б) 60°; в) 30°?
Под углом к плоскости проведена наклонная. Найдите , если известно, что проекция наклонной вдвое меньше самой наклонной.
Из точки А, удалённой от плоскости на расстояние d, проведены к этой плоскости наклонные АВ и АС под углом 30° к плоскости. Их проекции на плоскость образуют угол в 120°. Найдите ВС.
Самостоятельная работа
Вариант I
Из точки S к плоскости проведена наклонная SA. Найдите длину наклонной и её проекции, если точка S удалена от плоскости на 6 см, а наклонная образует с плоскостью угол 30°.
Через гипотенузу АВ прямоугольного треугольника ABC проведена плоскость . Найдите угол наклона катета ВС к плоскости , если АС = 24 дм, АВ = 26 дм, а точка С удалена от плоскости на 5 дм.
Из точки к плоскости проведены две наклонные. Найдите расстояние от данной точки до плоскости, если наклонные образуют с плоскостью углы, равные 30°, между собой – угол 60°, а расстояние между основаниями наклонных равно 8 дм.
Вариант II
Из точки S к плоскости проведена наклонная SA. Найдите длину проекции наклонной и расстояние от точки S до плоскости , если наклонная равна 6 см и образует с плоскостью угол 60°.
Через катет АВ прямоугольного треугольника ABC (А = 90°) проведена плоскость . Найдите угол наклона гипотенузы к плоскости , если АС = 6 дм, АВ = 8 дм, а точка С удалена от плоскости на 5 дм.
Из точки к плоскости проведены две наклонные. Найдите расстояние между основаниями наклонных, если данная точка удалена от плоскости на 2√2 дм, а наклонные образуют с плоскостью углы, равные 45°, между собой – прямой угол.
Контрольные вопросы:
1.Что такое угол между пересекающимися прямыми?
2.Что такое угол между скрещивающимися прямыми?
3.Что такое проекция прямой на плоскость?
4.Как определяется угол между прямой и плоскостью?
Задание на дом
[3] с. 133-135, 141-145, №420; 422