3.3. Расчет косвенных затрат на производство при I-м уровне цен на основные ресурсы

Косвенные (условно-постоянные) затраты (З_{пост i}) при i-м уровне цен на ресурсы рассчитывают как произведение коэффициента косвенных затрат (К_кос) (см. табл. 6) на годовой фонд прямой заработной платы основных рабочих при i-м состоянии «внешней среды» (ПЗП_i):

З_{пост i} = К_кос·ПЗП_i . (3.3.1)

З_{пост 1} = 2763189 грн.

З_{пост 2} = 4605315 грн.

3.4. Определение оптимальных программ выпуска продукции при различных состояниях «внешней среды»

При условии полной определенности i-го состояния «внешней среды», которое характеризуется вектором уровня цен на ресурсы и готовую продукцию:

. (3.4.1)

Оптимальная программа выпуска определяется решением задачи линейного программирования, сформулированной в подразд. 3.1:

(3.1.7)

которая может быть представлена в следующей развернутой форме:

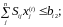
где – вектор переменных x_j, характеризующих объёмы производства изделий

– вектор коэффициентов целевой функции при i-м состоянии «внешней среды» ( );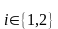

– вектор констант ограничений при i-м состоянии «внешней среды» ( ): b₁ = Т_год , b_i2 = D - З_{пост i} ,

– матрица технико-экономических характеристик t_j, S_ij производства изделий при i-м состоянии «внешней среды»,

Целевая функция для первого уровня цен товаров будет иметь вид:

7870x₁+ 7043x₂+ 4878x₃+ 3056x₄+ 2222x₅  max

при следующих ограничениях:

200x₁+300x₂+400x₃+500x₄+700x₅ ≤ 1100000

9837x₁+7825x₂+6969x₃+6112x₄+5554x₅ ≤ 5736811

Представленная задача линейного программирования, имеющая только два ограничения, может быть решена графоаналитическим методом с помощью использования двойственной задачи, алгоритм составления которой следующий:

Целевая функция двойственной задачи образуется как скалярное произведение вектора констант ограничений исходной (прямой) задачи и вектора новых переменных, размерность которого соответствует числу ограничений прямой задачи:

(3.4.2)

Критерий оптимальности задается диаметрально противоположным критерию прямой задачи:

. (3.4.3)

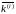Система ограничений двойственной задачи получается, если заданную матрицу A_i умножить слева на вектор новых переменных , в качестве вектора констант ограничений взять вектор коэффициентов целевой функции прямой задачи, а знак неравенства поменять на противоположный

.

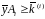Полученная двойственная задача линейного программирования

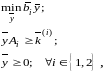(3.4.4)

которая может быть представлена в следующей развернутой форме:

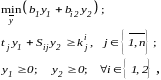(3.4.5)

решается графоаналитическим методом.

Итак, имеем двойственную функцию для первого типа товара:

1100000у₁ + 5736811у₂  min

При следующих ограничениях:

200у₁+ 9837у₂ ≥ 7870

300у₁+ 7825у₂ ≥ 7043

400у₁+ 6969у₂ ≥ 4878

500у₁ + 6112у₂ ≥ 3056

700у₁ + 5554у₂ ≥ 2222

Рис.3.4.1. Графоаналитическое представление двойственной функции линейного программирования первого уровня цен

Графическим методом получили точки с координатами: А (0; 0,9) и В (5;0,7), С (39; 0).

Подставляем координаты полученных точек в двойственную функцию

1100000у₁ + 5736811у₂ → min

А) 1100000*0 + 5736811*0,9 = 5163130

В) 1100000*5+ 5736811*0,7 = 9515768

С) 1100000*39+5736811*0=42900000

Получили минимальное значение двойственной функции в точке А, что соответствует количеству изделий х₂. Таким образом:

7825 * x₂ = 5163130

X₂ = 733

Для проверки правильности найденного решения использовали теорему двойственности. Допустимый вектор является решением задачи линейного программирования тогда и только тогда, когда существует такой допустимый вектор двойственной задачи, что значение целевых функций обеих задач на этих векторах равны.

Таким образом, в нашем случае выполняется равенство:

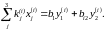(3.4.6)

7044* 733 = 1100000*0 + 3894685*0,9 = 5163130

Выполнение этого равенства гарантирует правильность полученного решения исходной задачи линейного программирования.

Для найденного решения ограничение по производственной мощности предприятия обращается в строгое неравенство

219900 < 1100000 и, с точки зрения практической интерпретации, это означает, что рассчитанные производственные мощности предприятия при i-м состоянии «внешней среды» будут недоиспользоваться, так как имеется их избыток.

Следовательно, численность работников предприятия должна быть пересчитана заново исходя из новой величины годовой трудоемкости

(3.4.7)

= 300*733=219900

Это повлечет за собой изменение условно-постоянных производственных затрат при i-м состоянии «внешней среды», что соответственно изменит решение исходной задачи линейного программирования.

ПЗП* = 283275 грн.

З*_пост. = 552387 грн.

D-З*_пост. = 7947613 грн.

Получаем новую функцию:

219900*у₁ + 7947613*у₂ → min

Подставляем координаты полученных точек А (0; 0,9) и В (5;0,7), С (39; 0) и определяем минимум функции:

А) 219900*0 + 7947613*0,9 = 7152851

В) 219900 *5 + 7947613*0,7 = 6662829

С) 219900*39 + 7947613*0=8576100

Минимальное значение функция принимает в точке A, что соответствует количеству продукции х₅.

Х₅= 510

Аналогично производим расчеты для второго уровня цен.

Целевая функция для второго уровня цен товаров будет иметь вид:

7999x₁+ 5874x₂+ 9582x₃+ 13122x₄+ 18327x₅  max

при следующих ограничениях:

200x₁+300x₂+400x₃+500x₄+700x₅ ≤ 1100000

12083x₁+9808x₂+8920x₃+8031x₄+7640x₅ ≤ 3894685

Имеем двойственную функцию для второго типа товара:

1100000у₁ + 3894685у₂  min

При следующих ограничениях:

200у₁+ 12083у₂ ≥ 3625

300у₁+ 9808у₂ ≥ 4904

400у₁+ 8920у₂ ≥ 6244

500у₁ + 8031у₂ ≥ 6425

700у₁ + 7640у₂ ≥ 7640

Рис.3.4.2. Графоаналитическое представление двойственной функции линейного программирования второго уровня цен

Получили две точки с координатами: А (0; 1), В (6,8;4,1), С(14;0,08),D(18;0).

Подставляем координаты полученных точек в двойственную функцию

1100000у₁ + 3894685у₂  min

А) 1100000*0 + 3894685*1 = 3894685

В) 1100000*6,8+ 3894685*4,1=23448209

С) 1100000*14+3894685*0,08=15711575

D) 1100000*18+3894685*0 =19800000

Получили минимальное значение двойственной функции в точке А, что соответствует количеству изделий х₅. Таким образом:

7634*x₅ = 3894685

x₅ = 510

Для проверки правильности найденного решения использовали теорему двойственности.

7634 * 510 = 1100000*0 + 3894685*1 = 3894685.

Выполнение этого равенства означает правильность полученного решения исходной задачи линейного программирования.

Для найденного решения ограничение по производственной мощности предприятия обращается в строгое неравенство

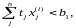
357000 < 1100 000.

Следовательно, численность работников предприятия должна быть пересчитана заново исходя из новой величины годовой трудоемкости:

= 700 * 510 = 357000

Это повлечет за собой изменение условно-постоянных производственных затрат при i-м состоянии «внешней среды», что соответственно изменит решение исходной задачи линейного программирования.

ПЗП* = 766479 грн.

З*_пост. = 1494634 грн.

D-З*_пост. = 7005366 грн.

Получаем новую функцию:

357000у₁ + 7005366 у₂ → min

Подставляем координаты рассчитанных точек А (0; 1), В (6,8;4,1), С(14;0,08), D(18;0) и определяем минимум функции.

А) 357000*0 + 7005366*1 = 7005366

В) 357000*6,8+ 7005366*4,1=31149600

С) 357000*14 + 7005366*0,08=11162722

D) 357000*18 +7005366*0=6426000

Минимальное значение функция принимает в точке А, что соответствует количеству продукции х₂ и х₅.

x₅ = 510.