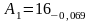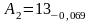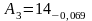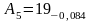Обратная задача
Способ равноточных допусков (метод одного класса точности).
Условно принимаем, что возрастание линейного размера допуска имеет ту же закономерность, что и возрастание допуска диаметра, а именно для 5-17 квалитетов.
i
= 0,45
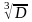 +
0,001D
– величина номинального допуска , где
D
в (мм), i
в (мкм).
+
0,001D
– величина номинального допуска , где
D
в (мм), i
в (мкм).
Номинальные верхние отклонения единичного допуска см. в таблице 2
Таблица 2.
Номинальные верхние отклонения единичного допуска
Обозначение допуска |
IT5 |
IT6 |
IT7 |
IT8 |
IT9 |
IT10 |
IT11 |
IT12 |
IT13 |
IT14 |
IT15 |
IT16 |
Значение допуска |
7i |
10i |
16i |
25i |
40i |
64i |
100i |
160i |
250i |
400i |
640i |
1000i |
Таким образом , в общем виде
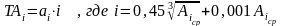
Значения i для основных интервалов в диапазоне до 400 мм приведены в таблице 3.
Таблица 3
Значения I для основных интервалов в диапазоне до 500 мм
Интервалы диаметров, мм |
i = 0,45 + 0,001D |
|||||||||||
3 |
3-6 |
6-10 |
10-18 |
18-30 |
30-50 |
50-80 |
80-120 |
120-180 |
180-250 |
250-315 |
315-400 |
|
Значения i, мкм |
0,55 |
0,73 |
0,90 |
1,08 |
1,31 |
1,56 |
1,86 |
2,51 |
2,52 |
2,9 |
3,23 |
3,54 |
TN
=
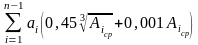 , где
, где
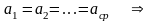
TN
=
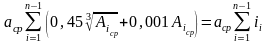
Откуда
находим, что
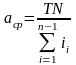 . Эта величина определяет по какому
квалитету нужно обрабатывать деталь.
. Эта величина определяет по какому
квалитету нужно обрабатывать деталь.
N = , TN = 120-(-380)=500
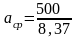 =
59,73 , поэтому выбираем 10квалитет с
единичным допуском 64.
=
59,73 , поэтому выбираем 10квалитет с
единичным допуском 64.
Для

Назначим отклонения всех составляющих охватываемых размеров с “ минусом ” (как для основного вала) и определим отклонения охватывающего размера из формул:
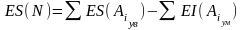
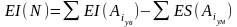
Причем
разницу в 42 мкм вносим в допуск на
=22
, как на самый большой номинальный из
охватываемых размеров, т.е. получим
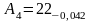 .
.
Далее по формулам найдем отклонения для :
500
=
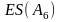 -
(-69-69-69-42-84) ,
=500-167=333
-
(-69-69-69-42-84) ,
=500-167=333
0
=
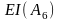 -
0
=
0
-
0
=
0
Получили,
что
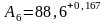
Таблица 4
Таблица результатов вычислений.
|
i ,мкм |
ТА |
, мм |
=16 |
1,08 |
69 |
|
=13 |
1,08 |
69 |
|
=14 |
1,08 |
69 |
|
=22 |
1,31 |
84 |
|
=19 |
1,31 |
84 |
|
=88,6 |
2,51 |
167 |
|
|
8,37 |
542 |
500 |

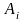 ном.
, мм
ном.
, мм
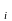 ,
мкм
,
мкм