
7-9 сыныптардағы алгебра курсын қайталауға арналған жаттығулар
Өрнекті ықшамдаңдар:
А) -
-
Ә)
Б){ }:
}: ;
;
В)
{ }:
}: ;
;
Г) +
+ ;
;
Ғ) ;
;
Д)25√b-0.5√4b+100√0.16b;
Е)√94a+3√242a-17√512a.
2. Теңдеуді шешіңдер:
А)
Ә)
Б)
В)
Г) ;
;
Ғ) ;
;
Д)
Е)
3. Теңдеудің түбірлерін табыңдар:
А) Ә)
Ә)
Б)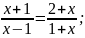 В)
В)
Г) ;
Ғ)
;
Ғ) ;
;
Д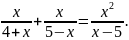
4. Теңдеулер жүйесін шешіңдер:
А)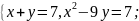 Ә)
Ә)
Б)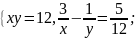 В)
В) .
.
5. Теңдеулер жүйесңн графикалық тәсілмен шешіңдер:
А) Ә)
Ә)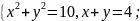
Б) В)
В) .
.
6. Теңсіздікті квадраттық функцияның графигі көмегімен және интервалдар әдісімен шешіңдер:
А) Ә)
Ә)
Б) В)
В) +5
+5 .
.
7. Теңсіздікті шешіңдер:
А) Ә)
Ә) Б)
Б)
В) Г)
Г) ;
Г)
;
Г) ;
;
8. Теңсіздікті қанағаттандыратын ең кіші бұтін санды табыңдар:
А) Ә)
Ә)
Б) В
В .
.
8. Теңсіздікті қанағаттандыратын ең үлкен бұтін санды табыңдар:
А) Ә)
Ә)
Б) В
В .
.
10. Теңсіздік жүйесін шешіңдер:
А) Ә)
Ә)
Б) В)
В) .
.
11. Теңсіздіктер жүйесімен берілген нүктелер жиынын координаталық жазықтықта кескіндеңдер:
А) Ә)
Ә)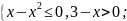
Б) В)
В)
Г) ;
Ғ)
;
Ғ) .
.
12. Функцияның нрафигін салыңдар және мәндер жиынын көрсетіңдер:
А) Ә)
Ә)
Б) В)
В)
Г)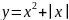 ;
Ғ)
;
Ғ) .
.
13. а) Бірінші натурал сан екінші натурал санның 75%-ына, ал олардың көбейтіндісінің мәні 1200-ге тең болатын екі натурал санды табыңдар.
ә)
Егер бөлшектің алымын екіге, ал бөлімін
үшке арттырса, онда берілген бөлшектен
 артық бөлшек шығады. Бастапқы бөлшекті
табыңдар.
артық бөлшек шығады. Бастапқы бөлшекті
табыңдар.
б) Екі таңбалы санның цифрларының қосындысының мәні 9-ға, ал цифрларының квадраттарының айырымының мәні 27-ге тең. Берілген екі таңбалы санды табыңдар.
в) Катер өзен ағысымен 36км, ал өзен ағысына қарсы 48км жүріп, барлық жолға 6 сағ уақыт жіберді. Егер өзен ағысының жылдамдығы 3 км/сағ болса, онда катердің меншікті жылдамдығы қандай?
г) Аралығы 180 км жолға бірінші пойыз екінші пойызға қарағанда 1,5 сағ артық уақыт жібереді. Егер пойыз 3 сағ-та бірге 162 км аралықта жүзсе, онда әр пойыздың жылдамдығы қандай?
14. а)3,2; 4; 4,8;... арифметикалық прогрессияның айырымын, тоғызыншы мүшесін және алғашқы он мүшесінің қосындысының мәнін табыңдар.
ә) 40; 39,6; 39,2; ... арифметикалық прогрессияның жетінші мұшесін және алғашқы жиырма мүшесінің қосындысының мәнін табыңдар.
б) Арифметикалық прогрессияның алтыншы мүшесі 35-ке, ал алғашқы сегіз мүшесінің қосындысының мәні 220-ға тең. Прогрессияның бірінші мүшесі мен айырымын табыңдар.
в) Арифметикалық прогрессияның екінші және сегізінші мүшелерінің айырымының мәні – 60-қа, ал үшінші және жетінші мүшелерінің қосындысының мәні – 40-қа тең. Прогрессияның бірінші мүшесін табыңдар.
15. а) 1,5; 3; 6; ... геометриялық прогрессиясының еселігін, жетінші мүшесін және алғашқы сегіз мүшесінің қосындысының мәнін табыңдар.
ә)
 ;
-2; 6; ... геометриялық прогрессияның
бесінші мүшесін және алғашқы алты
мүшесінің қосындысының мәнін табыңдар.
;
-2; 6; ... геометриялық прогрессияның
бесінші мүшесін және алғашқы алты
мүшесінің қосындысының мәнін табыңдар.
б) Геометриялық прогрессияның бесінші мүшесі 8-ге, ал алғашқы үш мүшесінің қосындысының мәні 112-ге тең. Прогрессияның бірінші мүшесі мен еселігін табыңдар.
в)
Геометриялық прогрессияның бесінші
және алтыншы мүшелерінің қосындысының
мәні
 -ке,
ал үшінші және бірінші айырымыныі мәні
24-ке тең. Прогрессияның бірінші мүшесін
табыңдар.
-ке,
ал үшінші және бірінші айырымыныі мәні
24-ке тең. Прогрессияның бірінші мүшесін
табыңдар.
16. Өрнектің мәнін табыңдар:
а)

ә)

б)
-
в)

г)
-
ғ) .
.
17.
а)
 және
және
 және
және
 -ның
мәндерін табыңдар.
-ның
мәндерін табыңдар.
ә) және
және
 және
және
 -ның
мәндерін табыңдар.
-ның
мәндерін табыңдар.
18. Өрнекті ықшамдаңдар:
а) ;
ә)
;
ә)
 ;
;
б)
 ;
в)
;
в)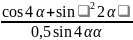 ;
;
г)
 ;
ғ)
;
ғ)
 ;
;
д)
 е)
е)

19. Тепе-теңдікті дәлелдеңдер:
а)
ә)
б)

в)
І тарау. ФУНКЦИЯ, ОНЫҢ ҚАСИЕТТЕРІ ЖӘНЕ ШГРАФИГІ
Нақты сандар жиыны, шамалар, жиын, айнымалы, сәйкестік, координаталар жазықтығы, нүктенің координаталары, график.
Осы тақырыпты оқу барысында сендер нені үйренесіңдер?
Бұл тақырыпты игеру барысында функция ұғымы, оның анықталу облысы, мәндерінің жиыны, графигі, берілу тәсілдері (кестелік, графиктік және аналитикалық) бойынша білім, билік, дағдыларыңды дамытасыңдар.
Математикада өте мағызды және күрделі ұғымдардың бірі – функция ұғымы. Сендер 7-9 сыныптардың алгебра курсынан кейбір элементар функциялармен таныссыңдар. Енді функция ұғымын тереңірек қарастырамыз. Алдымен функция ұғымына қатысты шамалардың түрлеріне тоқтайық. Шамалар тұрақты және айнымалы болып екіге бөлінеді. Тұрақты шамалар абсолют тұрақты және параметр, ал айнымалылар тәуелді және тәуелсіз болып бөлінеді.
Анықтама: Белгілі бір сандық мән қабылдайтыншаманы тұрақты шама деп атайды.
Анықтама: Кез келген жағдайда тек қана бір сандық мән қабылдайтын шаманы абсолют тұрақты шама деп атайды.
Мысалы,
кез келген шеңбер ұзындығын, оның
диаметріне қатынасы тұрақты
 санын береді. Ол иррационал сан, оның
0,01 дәлдікпен есептегендегі жуық мәні
3,14-ке теі екені белгілі.
санын береді. Ол иррационал сан, оның
0,01 дәлдікпен есептегендегі жуық мәні
3,14-ке теі екені белгілі.
Анықтама: Берілген жағдайларда ғана белгілі бір сандық мәнін сақтайтын тұрақты шаманы параметр деп атайды.
Анықтама: Әр түрлі сандық мәндер қабылдайтын шаманы айнымалы шама деп атайды.
Анықтама: Сандық мәндерін басқа айнымалыға тәуелсіз қабылдайтын айнымалыны тәуелсіз айнымалы шама деп атайды.
Анықтама: Сандық мәндерін басқа айнымалыға тәуелді қабылдайтын айнымалыны тәуелді айнымалы шама деп атайды.
Мысалы: бірқалыпты қозғалыстағы дененің t уақыт ішіндегі жүрген жолы s=v*t формуласымен анықталатыны белгілі. Бұл формуладағы s дененің жүрген жолы және t уақыт – айнымалы шамалар. s айнымалысы t –ға тәуелді, ал v- бірқалыпты қозғалыстағы дененің тұрақты жылдамдығы, яғни v- пераметр.
Енді функция ұғымының анықтамасын берейік.
Анықтама: Х жиынындағы х-тің әрбір мәніне Ү жиынның нақты бір у мәнін сәйкес қоятын ереже немесе заңдылық функция деп аталады.
Функцияны у = f{x), у = ф (х), у = g(x) жене т.с.с. белілейда, мұндағы х — тәуелсіз айнымалы немесе функцияның аргументі у - тәуелді айнымалы немесе функция, f, ф, g жене т.с.с. — ереже немесе заңдылык.
Функция белгілі 6ip мән кабылдайтын теуелсіз айнымалының мәндер жиынын функцияныц аныкталу облысы (D), ал аныкталу облысынан алынған әp6ip теуелсіз айнымалыға сейкес табылган (функцияның мәндерін оның мәндер жиыны (Е) деп атайды.
Сонда аныктамадагы X жиыны функцияның аныкталу облысы, Y жиыны функция мендерінің жиыны болады.
Функцияның жоғарыда берілген аныктамасына сейкес темендеп үш жағдайды анықтай білу керек:
1) функцияныц D (/) аныкталу облысын;
2) х пен у айнымалыларыныц арасьшдагы / ереже немесе зац-дыльщты;
3) функцияныц Е (/) мендер жиынын. Мысалдар келтарейпс.
2 I—
1-мысал. а) у = х2 + 2х - 5; е) у = —^-7; б) у = у/х функциясыныц
аныкталу облысын табайык.
Шешуй а)г/ = х2 + 2х-5 функциясы кепмуше (бутш рациона л (функция) болгандыктан, аргументтщ кез келген мешнде аныкталады. Демек, функцияныц аныкталу облысы барлык накты сандар жиыны, ягни D (f) = R.
2
е)У=
х+
i
белшек-рационалфункция,оныцбел1м1
х
+ 1
Ф0болуы
шарт немесе хф —\. Демек, х = -1 меншде функция аныкталмаган. Сонда бершген функцияныц аныкталу облысы -1 санынан баска барлык накты сандар немесе D (/) = (-<*>; -1) и (-1; +°°);
б) у = Jx функциясыныц аныкталу облысын табу ушш Ty6ip 1ш1ндег1 орнект1 Tepic емес деп аламыз, ягни х > 0. Будан D(f) = [0; +«.).
Жауабы: a) R; е) (-°°;-1)и(-1;+°°); б) [0; +<»). 4
2-мысал.
у = 3
+ _
1
функциясыныц аныкталу облысын жене
мендершщ жиынын табайык.
Шешу1 Алдымен функцияныц аныкталу облысын аныктаймыз. Бул функция туракты жене белшек-рационал функцияныц крсын-дысына тец. Туракты функция барлык накты сандар жиынында аныкталган. Демек, бершген функцияныц аныкталу облысын табу ушш белшек рационал функцияныц аныкталу облысын табу керек. 4
Ал
1
ернеи х
Ф 1
жагдайда аныкталады. Олай болса,
бершгенфункцияныц аньщталу облысы
туракты жене белшек-рационал функцияныц
аныкталу облыстарыныц киылысуына тец
болады, ЯГНИ D
(/)
= (-оо; 1) и (1; +°°).
4
Ещц
функцияныц мендершщ жиынын табайык.
_
^
*
0 болган-
444 дыктан, и = 3 + -—г ф 3 жене -«> <-- < 0, жене 0 <-- < +«э
" X - L х - 1 X - 1
екеш анык. Демек, функцияныц мендершщ жиыны 3-тен баска барлык накты сандар жиыны, ягни Е (/) = (-оо; 3) и (3; +°°).
Жауабы: D (/) = (-~; 1) и (1; +~); Е (/) = (-оо; 3) и (3; +«»).
3-мысал. у = 3 sin х функциясыныц мвндер жиынын табайык.
Illeuiyi. у = sinx функциясыныц мендер жиыны [-1; 1] кесшдас1 екеш белгип, ягни бер1лген функцияныц мендер жиынын табу ушш -1 < sin х < 1 кос тецс1здц1не кешем1з. Ещц кос тецйзджтщ ep6ip белтн 3-ке квбейтем1з: -3 < 3 sin х < 3. Демек, бер1лген функцияныц мвндер жиыны [-3; 3] кесшдий.
Жауабы: [-3; 3].
Жалпы, функцияныц аныкталу облысын табу жолдарын келтарейж:
1) бутш рационал функцияныц (квпмуше туршде бершу!) аныкталу облысы барлык накты сандар жиыны;
2) белшек-рационал функцияныц аныкталу облысы бвлшектщ бел1м1 нелге тец болатын аргумент мендершен езге барлык накты сандар жиыны;
3) егер функция иррационал врнек туршде бер1лсе, онда функцияныц аныкталу облысы туб1рдщ дереже керсеткншне теуелд1, ягни туб1рдщ дереже керсеткнш так болса, онда оныц аныкталу облысы — бел1м1 нолге айналмайтын сандардан баска барлык накты сандар жиыны; ал, егер туб1рдщ дереже керсеткпш жуп болса, онда ту-6ip астындагы ернек тернз емес (туб1р ернектщ тек алымында болса) немесе оц (туб1р — бвл1мшде) болатын аргумент мендершщ жиыны;
4) курдел1 трансцендент функциялардыц аныкталу облыстары сейкес элементар функциялардыц аныкталу облыстары нешзшде табылады.
5) егер функция ер турл1 функциялардыц алгебралык косындысы туршде 6epince, онда оныц аныкталу облысы косылгыш функциялардыц аныкталу облыстарыныц киылысуына тец.
Координаталык жазыктьщтагы абсциссалары теуелс1з айны-малы х, ал ординаталары теуелда айнымалы у болатын, (хг, Дх)) нуктелерпнц геометриялык орны у = Дх) функциясыныц графип болатыны белгип (1-сурет).
2-суретте бершген кисык функцияныц графип болмайды, ейткеш хг аргументше функцияныц б1рнеше мендерд., ягни уг, у2, у3 мендер1 сейкес.
Функциялардыц кестелж, графиктж жене аналитикалык твс1л-дермен бершетпп белгип.

1-сурет 2-сурет
Мунда бгршпп жолда i уапым Колда уакыт мендерше сейкес аныкталган Т ауа температурасы. Демек, кестеде температура мен теулж мезплшщ арасындагы тоуелдипк керсетшген.
5-мысал. (Функцияныц графиктж твсшмен бершуь). 3-суретте BepinreH функцияныц графип бойынша оныц мына касиеттерш
Гмшкауга болады:
1) функцияныц аныкталу облысы D (/) = [-5; 5];
2) функцияныц мендер жиыны E(f) = [-3; 3];
3) функцияныц нвлдер1: х = -3; 0; 4;
4) Д-5) = 1, /(0) = 0, /(2) = 2, /(3) = 3; /(4) = 0; /(5) = -3. Кунделжта ем1рде, практикада, гылымныц барлык салаларында,
атап айтсак, физика, химия, медицина, метереология т.с.с. графиктж т.гсш кеншен колданылады. Метерео-погияда колданылатьш курал — барограф атмосфералык кысымныц ез-геру графил барограмманы сызса, ал медицинада электрокардиограф жу-ректщ согуын т1ркеп, оны график туршде (электрокардиограмма) бе-реда. График бойынша етш жаткан процесс туралы жалпы сипаттама жасауга болады.
Emii ep6ip тесшге мысалдар карастырайык.
4-мысал. Функцияныц кестелж твсшмен бершу!. Кыс аиларыныц Ирщдеп 6ip твулж шпнде ауа температурасыныц взгеру кестесш
/ (саг) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
'/'(С) |
-12 |
-15 |
-16 |
-12 |
-6 |
-4 |
-6 - |
-9 |
-11 |
Мунда бгршпп жолда i уапым Колда уакыт мендерше сейкес аныкталган Т ауа температурасы. Демек, кестеде температура мен теулж мезплшщ арасындагы тоуелдипк керсетшген.
5-мысал. (Функцияныц графиктж твсшмен бершуь). 3-суретте BepinreH функцияныц графип бойынша оныц мына касиеттерш
 Гмшкауга
болады:
Гмшкауга
болады:
1) функцияныц аныкталу облысы D (/) = [-5; 5];
2) функцияныц мендер жиыны E(f) = [-3; 3];
3) функцияныц нвлдер1: х = -3; 0; 4;
4) Д-5) = 1, /(0) = 0, /(2) = 2, /(3) = 3; /(4) = 0; /(5) = -3. Кунделжта ем1рде, практикада, гылымныц барлык салаларында,
атап айтсак, физика, химия, медицина, метереология т.с.с. графиктж т.гсш кеншен колданылады. Метерео-погияда колданылатьш курал — барограф атмосфералык кысымныц ез-геру графил барограмманы сызса, ал медицинада электрокардиограф жу-ректщ согуын т1ркеп, оны график туршде (электрокардиограмма) бе-реда. График бойынша етш жаткан процесс туралы жалпы сипаттама жасауга болады. 3-сурет
6-мысал. Функцияныц аналитикалык тесшмен 6epuiyi. 1 -х
a) f(x) = х2 + ——; в) Ах) = sinx + х аналитикалык тесшмен бершген функциялар.
О вздер1н,е белгШ аналитикалык тэсшмен бершген элементар функция-ларга мысалдар келтлрщдер.
Ендд функциянын бершу твсшдершщ вркдйсысыныц ерекшелпс-терше токталайык:
1) кестелгк тэсшмен бершудщ ерекшелЫ— аргументтщ мвндерше свйкес функциянын мвндер1 катар бершед1;
2) графиктт твсшдщ ерекшелЫ — кернекшшшде;
3) аналитикалык; твсш функцияны толык зерттеу ушш ете ынгайлы.
1. Функциянын аныктамасындагы ереже, зандыльщ дегенд1 калай тусл.-несщдер? Мысал келпрщдер.
2. Функцияныц аныкталу облысына кандай жиын свйкес койылады?
3. Функциянын аныкталу облысын табу yniiH кандай шарттар карасты-рылады. Мысалдар келпрщдер.
4. Функциянын графигш у = Ь жене х = а тузулер1 б1рнеше нуктеде киюуы мумкш бе? Жауабын тусшддрщдер.
Жаттыгулар А
20. у = f(x) функциясыньщ бершген нуктелердеп мвндерш табындар: a) fix) = 2x2 + 3, х = -1; 2,5; 3; в) f(x) = | - 5х, х = -0,5; ^; 0;
бШ*)=;^з +2, х=4;5; |; B)f(x)=j~, х=-1;0; -\.
21. а) /(х) = 2Х2; в) f(x) = 2х2 + Зх-4; б) /(х) = ; в) f(x) = \
функциясыньщ /(-2), ffij, /(1) мвндерш табындар.
22. Функцияныц аныкталу облысын табындар:
a) g (х) = 2,5х - 4,2; в) g (х) = Зх2 - 7х + 4;
б)£(х)=^; в)£(х)=£+3.
1 з
23. /(х) = -— 4х жене g (х) = —Ь 7:
Ах х
Я)/(1) + |(1)+^(4); eyf{l)*hi~l)> б)/(-2)-^(3); в) 4 / (2) + 3g\ ^ J ернегшщ менш есептецдер.
14. 4-суреттеп кай график функцияныц графип болмайды?
У, |
1 |
О |
*х |
а
6
4-сурет
25./(х) = 2х2-Зх+4 функциясы бершген. Аргументтщ кандай мпидершде бершген функция a) f(x) = 4; э) fix) = 9; б) f(x) = 18; n) /'(х) = 6 мвндерш кабылдайды?
26. f(x) функциясыньщ графип бершген (5-сурет).
а) Функцияныц аныкталу облысын; в) функцияныц мвндер жиынын;
б) функцияныц нелш;
в) /(-4), /40), /(4) мвндерш табындар.
27. fix) = x2 - 5x + 2 функциясы берьлген. f(2) = -4, /(-1) = Щ тещцктершщ орындалатынын тексерщдер.
28. Бершген нуктелердел. у = g(x) функциясыныц мвндерш табьщцар: j a)g(x) = 2xi-~, х, = 4; *о=2: *L=l.fi:
|
1 _ 4 ' |
*2 |
= 2; |
х3 1,5; |
|
= 4; |
% |
= 2; |
х3= -% |
|
—71. |
|
л |
|
Xj |
|
*2 |
|
X =-- • |
«1 |
|
*2 |
= t.,+ 2; |
2 ^3 - ( • |
б) g(x) = 2 + sin 2х, ^i=f; х2 = \' *3=_f;
2 2
в) g(x) = —2 + Зх, xl = t; x2 = t + 2; х3 = -.
29. Функцияньщ аныкталу облысын табындар: а) Дх) = 0,5 - л/х-3 ; в) Дх) = л/2х2-7х+ 5 ;
б)Д*)
=
4Й;
***il4j-9f
|
30. Функцияныц аныкталу облысын жене мвндер жиынын табындар:
а) г/ = х2 - 4х + 4; в) у = - - 5;
б) у = | - 2 sinx; в) у = 5cos ~.
3 4
31. f(x) = — 2Х2 жене g(x) =— + 2 функциялары бершген.
а)Л-3) + £<-2) + /(i); e)f(0,5)-g[\y,
б) / [|] ' - ! в) 3/(а) + 4g-(a) функциясыныц менде-
рш табындар.
32. Af-|; о), в(^; 2J, С(-1; 1), D(3; 0,5) нуктелершщ кайсысы у = 2Х2 + х функциясыныц графигше тиклт.?
33. Тлктертбурыштыц eHi 5 см-ге тец. Оныц ауданыныц узындыгына теуелдшггш керсетётш функцияны жазындар.
34. Шецбер радиусыныц оныц узь*нДыгына теуелддлтн керсетётш функцияны жазындар. t
% 2. ФУНКЦИЯНЬЩ ГРАФИКТЕРШ КАРАПАЙЫМ ТТРЛЕНД1РУ
Сызыцтыц функция, квадраттык функция, Kepi пропорцио-налдык теуелдшт жене олардыц графиктерг, фигураларды турлендЬру турлерЬ, нукте мен гщзуге карагандагы симметрия, параллель квииру, гомотетия.
