3.3 Задача ползучести
Необходимо определить величину прогиба бетонного стержня для каждой равномерно распределённой нагрузки в разные моменты времени с помощью уравнения выведенного из математической модели деформаций ползучести бетонного стержня.
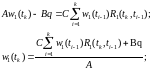
Где к- число шагов условной единицы времени, принимаем равное 10
Аналогично вычисляем прогиб при оставшихся нагрузках:
Таблица 5 – Результаты решения задачи ползучести для бетонного стержня
|
W1(t0) |
W1(t1) |
W1(t2) |
W1(t3) |
W1(t4) |
W1(t5) |
W1(t6) |
W1(t7) |
W1(t8) |
W1(t9) |
W1(t10) |
R1 |
0,02011 |
0,02093 |
0,021784 |
0,022674 |
0,023599 |
0,024562 |
0,025564 |
0,026608 |
0,027693 |
0,028824 |
0,03 |
q1 |
0,196184 |
0,200129 |
0,204318 |
0,208769 |
0,213502 |
0,218541 |
0,223909 |
0,229633 |
0,235743 |
0,242271 |
0,249254 |
q2 |
0,23425 |
0,23896 |
0,243962 |
0,249276 |
0,254928 |
0,260944 |
0,267354 |
0,274188 |
0,281484 |
0,289279 |
0,297617 |
q3 |
0,272315 |
0,277791 |
0,283605 |
0,289784 |
0,296354 |
0,303348 |
0,310799 |
0,318744 |
0,327225 |
0,336287 |
0,34598 |
q4 |
0,310381 |
0,316622 |
0,323249 |
0,330291 |
0,33778 |
0,345751 |
0,354243 |
0,363299 |
0,372966 |
0,383295 |
0,394343 |
q5 |
0,348446 |
0,355453 |
0,362893 |
0,370798 |
0,379206 |
0,388155 |
0,397688 |
0,407855 |
0,418707 |
0,430303 |
0,442705 |
q6 |
0,386512 |
0,394284 |
0,402537 |
0,411306 |
0,420632 |
0,430558 |
0,441133 |
0,452411 |
0,464448 |
0,47731 |
0,491068 |
Анализ полученных результатов
4.1 Линейно-упругая задача
Рисунок 2 – график зависимости прогиба стержня (бетонного и стального) от приложенных внешних нагрузок
Проанализировав график зависимости величины прогиба от величины приложенной нагрузки, можно заключить, что при использовании математической модели линейно-упругих деформаций, конечная зависимость действительно линейна, что только подтверждает название математической модели.
4.2 Нелинейно-упругая задача
Рисунок 3 – график зависимости прогиба стального стержня от приложенных внешних нагрузок
Проанализировав график зависимости величины прогиба от величины приложенной нагрузки, можно заключить, что при использовании математической модели нелинейно-упругих деформаций, конечная зависимость действительно нелинейна, что только подтверждает название математической модели.