Министерство образования и науки Российской Федерации

Санкт-Петербургский государственный архитектурно-строительный университет

Кафедра Прикладной математики и информатики

Дисциплина: Математическое моделирование

Курсовая работа

по теме

Изучение влияния внешних нагрузок на деформации строительных конструкций

Вариант №27

Выполнил студент группы 1-См-I

Хренов Г. М.

Принял преподаватель

Семёнов А.А.

Санкт-Петербург

2015 г.

Содержание

Введение 3

1. Описание математических моделей 4

1.1 Модель линейно-упругих деформаций 4

1.2 Модель нелинейно-упругих деформаций 4

1.3 Модель деформаций, возникающих в результате ползучести 5

2. Исходные данные 6

3. Решение 7

3.1. Линейно-упругая задача 7

3.2. Нелинейно-упругая задача 8

3.3. Задача ползучести 10

4. Анализ полученных результатов 12

4.1. Линейно-упругая задача 12

4.2. Нелинейно-упругая задача 13

4.3. Задача ползучести 14

Заключение 15

Список использованной литературы 16

Введение

В данной курсовой работе рассмотрено влияние внешних нагрузок на деформации строительной конструкции на примере стержня, путём применения различных математических моделей, и постановки соответствующего вычислительного эксперимента.

Эксперимент заключается в поочерёдном приложении к стрежню распределённых нагрузок различной величины и определению прогиба в средней точке с помощью различных математических моделей. Для проведения эксперимента выбрано три математические модели:

1. Модель линейно-упругих деформаций

2. модель нелинейно-упругих деформаций

3. модель деформаций вызванных ползучестью материала

1. Описание применяемых моделей

1. Модель линейно-упругих деформаций:

Даная модель подразумевает линейную зависимость, где величина упругих деформации зависит от приложенной внешней нагрузки. В данной модели поведение стержня описывает закон Гука:

(1.1)

При этом функционал полной потенциальной энергии деформации равен разности между потенциальной энергией системы и работы внешних сил:

(1.2)

Продифференцировав данное уравнение по W и прировняв полученное выражение к нулю получаем:

(1.3)

Используя метод Ритца получаем:

(1.4)

2. Модель нелинейно-упругих деформаций:

Даная модель подразумевает наличие нелинейной зависимости между величиной деформаций и приложенной нагрузкой, и добавляет нелинейный член в функционал полной потенциальной энергии системы:

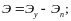(1.5)

(1.6)

Продифференцировав по неизвестной переменной и прировняв функционал полной потенциальной энергии деформации к нулю и проведя ряд математических преобразований получаем следующее уравнение:

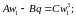
(1.7)

где:

(1.8)

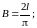(1.9)

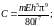(1.10)

Полученное уравнение можно решить с помощью метода итераций, полученное в результате значение подставляем в следующее уравнение и получаем прогиб в средней точке стержня:

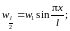
(1.11)

1.3 Модель деформаций, возникающих в результате ползучести материала:

Даная модель подразумевает изменение величины прогиба стержня под действием статической нагрузки с течением времени из-за ползучести материала, из-за чего необходимо ввести новую переменную (переменную времени), а также функции влияния времени на величину прогиба. В таком случае функционал полной потенциальной энергии системы принимает следующий вид:

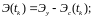(1.12)

(1.13)

Прировняв данное уравнение к нулю, получим:

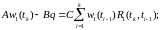
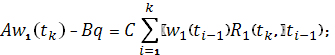(1.14)

Для решения полученного уравнения так же придётся воспользоваться методом итераций.