10. Үлгінің сәйкестігін тексеру

Үлгінің коэффициенттерін есептегеннен кейін және олардың маңыздылығын анықтағаннан соң үлгінің сәйкестігін тексереді.

Сәйкестік – бұл үлгінің кейбір аумақтарда талап етілетін дәлдікпен тәжірибелердің нйтижелерін алдын-ала айта алу мүмкіндігі.

Сәйкестік туралы болжамды F – Фишер өлшемінің көмегімен тексереді:

F= / ,

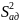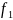мұндағы – бостандықтың -деңгейінің саны арқылы анықталған тәжірибенің дисперсиясы;

– жеткіліктілік дисперсиясы (қалдықтық дисперсия), эмпирикалық мәннің У алынған регрессия теңдігінен анықталған есептелген қатысты шашырауын сипаттайды.Сәйкестік дисперсиясын мына формула бойынша анықтайды:

= ,

мұндағы 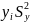– жеткіліктілік дисперсиясы (қалдықтық дисперсия), эмпирикалық мәннің У алынған регрессия теңдігінен анықталған есептелген қатысты шашырауын сипаттайды.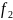 -бостандық деңгейлердің саны;

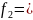N-r,

мұндағы r- статикалық маңызды коэффициенттер саны.

N-r= 16-9= 7.

Оңтайландыру параметрлерінің мәндерін есептейміз:

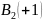= (+1) + (+1) + + (+1)+ 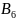(+1)+ (+1) + 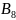(+1) + + (+1)=

=222,15+6,6-6,34+12,28+39,28-0,34+21,09+9,97-4,34=300,35;

=222,15-6,6-6,34+12,28+39,28+0,34-21,09+9,97+4,34=254,33;

=222,15+6,6+6,34+12,28+39,28-0,34+21,09-9,97+4,34=301,77;

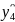=222,15-6,6+6,34+12,28+39,28+0,34-21,09-9,97-4,34=238,39;

=222,15+6,6-6,34-12,28+39,28-0,34-21,09-9,97+4,34=222,35;

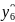=222,15-6,6-6,34-12,28+39,28+0,34+21,09-9,97-4,34=243,33;

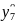=222,15+6,6+6,34-12,28+39,28-0,34-21,09+9,97-4,34=246,29;

=222,15-6,6+6,34-12,28+39,28+0,34+21,09+9,97+4,34=284,63;

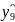=222,15+6,6-6,34+12,28-39,28+0,34+21,09-9,97+4,34=211,21;

=222,15-6,6-6,34+12,28-39,28-0,34-21,09-9,97-4,34=146,47;

=222,15+6,6+6,34+12,28-39,28+0,34+21,09+9,97-4,34=235,15;

=222,15-6,6+6,34+12,28-39,28-0,34-21,09+9,97+4,34=187,77;

=222,15+6,6-6,34-12,28-39,28+0,34-21,09+9,97-4,34=155,73;

=222,15-6,6-6,34-12,28-39,28-0,34+21,09+9,97+4,34=192,71;

=222,15+6,6+6,34-12,28-39,28+0,34-21,09-9,97+4,34=157,15;

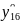=222,15-6,6+6,34-12,28-39,28-0,34+21,09-9,97-4,34=176,77.

=

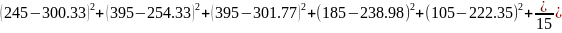
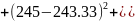
=10790.176.

Есептік Фишер өлшемін табамыз:

F= / .

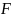= =1.435.

5-қосымшада берілген кесте [2] бойынша маңыздылық деңгейі 0,05 болғандағы F- Фишер өлшемінің мәнін табамыз.

-1= 16-1= 15;

N-r= 16-9= 7;

( α, , )=2,7.

Демек, үлгінің сәйкестігі туралы болжам маңыздылық деңгейі α= 0,05 болғанда қабылданады.

11. Алынған үлгіні пайдалануға қатысты шешімді қабылдау

Регрессияның сәйкес сызықтық теңдеуге арналған шешімді қабылдауды талқылаймыз [3]

Сызықтық үлгі сәйкес. Біздің жағдайда регрессияның кейбір коэффициенттері маңызды;

Егер оңтайландыру аумағы жақын болса, онда үш шешім болуы мүмкін: зерттеудің аяқталуы, екінші реттік жоспарларға көшу және көкжиекке қарай жылжу.

Екінші реттік жоспарлауға көшу оптимум аумағының математикалық сипаттамасын алуға және экстремумды табуға мүмкіндік береді. Біз екінші реттік жоспарларды құру сұрақтарын қарастырмасақ та ол мүмкіндікті де ескеруіміз керек.

Көкжиек бойынша қозғалу тәжірибенің аздаған қателігінде пайдаланылады, себебі үлкен қателік кезінде оңтайландыру параметрінің өсуін бекіту қиынға соғады.

Анықталмаған жағдайда немесе оптимумның қашықтатылған облысында шешім бір: градиент бойынша қозғалу.