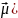3) Найдем оптимальную (по Парето) финансовую операцию.

Каждое решение имеет две характеристики – средний ожидаемый доход М (Q_i) – ячейки В48:В51 (рис.13) и средний ожидаемый риск R_i –ячейки Н48:Н51 (рис.13): I(8,35; 3,45); II(7,45;4,35); III(5,2; 6,6); IV(7,55;4,25).

Отметим найденные решения точками с координатами (М(Q_i); R_i) на плоскости: на оси абсцисс средний доход, а по оси ординат – средний риск. Получим четыре точки (рис. 14).

Рисунок 14 – Поиск оптимальной (по Парето) финансовой операции

Чем выше точка, тем более рисковая операция, чем правее точка, тем она более доходная. Значит нужно выбирать ниже и правее. В данном примере множество Парето состоит из первого решения.

Ответ. В условиях полной неопределенности правило Сэвиджа рекомендует первое, второе или четвертое решение, правило Вальда – первое или четвертое решение, правило Гурвица во всех трех случаях советует принять первое решение, а в условиях частичной неопределенности использовать только первое решение.

Задача 4.

Дан портфель из трех бумаг с доходностями μ₁ = 26%, μ₂ = 17%, μ₃ = 14% и ковариационной матрицей V = .

Найти портфель минимального риска с доходностью μ = 21% и его риск. Написать уравнение минимальной границы.

Решение.

Для нахождения портфеля предварительно надо вычислить:

- обратную матрицу V^-1;

- константы (при этом константы α, γ, 𝛿 – положительные числа):

- α = I^TV^-1I, β = I^TV^-1 = ^TV^-1I,

- γ = ^TV^-1 , 𝛿 = αγ – β²;

- λ = ; ν = .

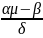Тогда портфель находится по формуле: Х = V^-1(λI + ν ).

Уравнение минимальной границы имеет вид:

σ =

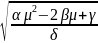
Все громоздкие вычисления проведем в MS Excel. Подготовим рабочий лист и внесем исходные данные (рис. 15).

Рисунок 15 - Исходные данные и шаблон для решения задачи

Заметим, что V является положительно определенной.

Введем зависимости.

Формула	Ячейка	Функция для вычисления
V-1	B6:D8	{=МОБР(В2:D4)}
ITV-1	B10:D10	{=МУМНОЖ(J2:L2;B6:D8)}
α = ITV-1I	G10	{=МУМНОЖ(B10:D10;H2:H4)}
β = ITV-1	C12	{=МУМНОЖ(B10:D10;F2:F4)}
TV-1	B15:D15	{=МУМНОЖ(J4:L4;B6:D8)}
γ = TV-1	G15	{=МУМНОЖ(B15:D15;F2:F4)}
𝛿 = αγ-β2	K7	=G10*G15-C12^2
λ = γ-βμ/𝛿	K9	=(G15-C12*F6)/K7
ν = αμ-β/𝛿	K11	=(G10*F6-C12)/K7
λI+ν	F18	=$K$9*B18+$K$11*D18
	F19:F20	Скопировать формулу из ячейки F18
X = V-1(λI+ν	С22:С24	{=МУМНОЖ(B6:D8;F18:F20)}
XT	H19:J19	{=ТРАНСП(C22:C24)}
XTV	H21:J21	{=МУМНОЖ(H19:J19;B2:D4)}
XTVX	H23	{=МУМНОЖ(H21:J21;C22:C24)}
σ	H25	=КОРЕНЬ(H23)

Теперь перенесем формулы в MS Excel (рис. 16).

Рисунок 16 – Результаты расчета портфеля минимального риска с доходностью 21%

В заключении запишем вид минимальной границы по формуле:

σ = .

Подставляя в нее найденные значения констант α=0,09; β=1,67; γ=31,09; 𝛿=0,12 получим

σ = = .

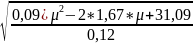Итак, минимальная граница имеет вид σ = .

Ответ. Таким образом, портфель минимального риска с доходностью μ = 27% равен Х = (0,538; 0,181; 0,281): необходимо взять 53,8% бумаг первого вида; 18,1% - второго и 28,1% - третьего вида.

Риск портфеля равен 4,31 и оказался меньше риска первой бумаги (σ₁=8), второй (σ₁=7) и третьей (σ₁=6) бумаг. При этом доходность портфеля μ=21% на 5% меньше доходности первой бумаги, на 4% больше доходности второй и на 7% больше доходности третьей бумаги.

Минимальная граница имеет вид σ = .

Задача 5.

Найти доходность портфеля облигаций, состоящего из двух видов облигаций по 150 и 70 штук с доходностью 30% и 20% с курсами 108% и 104% соответственно.

Решение.

Доходность портфеля облигаций находится по формуле:

ρ = 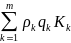/ 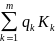, где

ρ_k – доходность облигации,

q_k – количество облигаций данного вида,

K_k – курс облигации.

По условию задачи ρ₁ = 0,3, q₁ = 150, К₁ = 108; ρ₂ = 0,2, q₂ = 70, К₂ = 104.

ρ = ≈ 0,269.

Ответ. Доходность портфеля облигаций, состоящего из двух видов облигаций по 150 и 70 штук с доходностью 30% и 20% с курсами 108% и 104% соответственно, равна ρ ≈ 0,269.