4.2.1. Потенциальная помехоустойчивость АМ. При АМ сигнал имеет вид

Находим частную производную

а среднее значение квадрата этой величины (средняя мощность)

Согласно выражению (4.1) спектральная плотность шума на выходе приемника

Поскольку она не зависит от частоты, то при из выражения (4.3) получим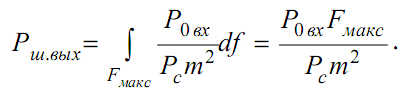

Тогда из выражения (4.5)

Билет 19

Основные понятия

Помехоустойчивостью называют способность системы правильно принимать информацию, несмотря на воздействия помех. Действие помехи проявляется в том, что принятый сигнал (а следовательно, информация) отличается от переданного. Степень соответствия принятой информации переданной называется достоверностью. Оценкой достоверности служит вероятность правильного приёма, равная отношению числа правильно принятых символов сообщений (знаков, цифр, элементов) к общему числу переданных символов при достаточно большом числе передаваемых сообщений. Обычно такое отношение подсчитывают за определённый промежуток времени. Иногда пользуются понятием потери достоверности, которую оценивают частостью ошибок:

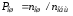, (3.1)

где – число неправильно принятых символов сообщений;

–общее число переданных символов сообщения.

3.2. Помехоустойчивость передачи дискретных элементарных сигналов

Для оценки помехоустойчивости дискретных (двоичных) элементарных сигналов используется вероятностный критерий.

Наиболее высокой помехоустойчивостью обладает так называемый идеальный приёмник Котельникова, который обеспечивает при данном способе передачи наилучшую помехоустойчивость, называемую потенциальной.

Потенциальная помехоустойчивость – это предельно допустимая помехоустойчивость, которая может быть обеспечена идеальным приёмником. Теория потенциальной помехоустойчивости развита для флуктуационных помех. Идея построения идеального приёмника заключается в том, что, зная, какие сигналы должны быть переданы, и имея их образцы, он сравнивает полученные сигналы по очереди с этими образцами [и] и, вычисляя энергию разности принятого сигнала и образца (величиныили), относит принятый сигнал к тому сигналу, для которого эта разность минимальна.

, (3.2)

. (3.3)

Если , то считаем принятым сигнал, а если– сигнал_.

Изменяя величину , можно регулировать соотношение вероятностей превращения одного сигнала в другой. Структурная схема идеального приёмника Котельникова приведена на рис. 3.1.

Помехоустойчивость идеального приёмника может быть рассчитана по формулам:

, (3.4)

. (3.5)

Здесь – табличная ограниченная функция, значения

которой приведены в прил. 1;

–величина, характеризующая потенциальную помехоустойчивость,

; (3.6)

–параметр, характеризующий пороговые свойства приёмника,

, (3.7)

где –удельное напряжение помехи в полосе частот 1 Гц

, (3.8)

где – пороговое значение сигнала;

–среднеквадратическое значение напряжения помехи;

–полоса пропускания приёмника.

Рис. 3.1. Структурная схема идеального приёмника Котельникова

87

При симметричном канале, когда вероятность подавления команды и образования ложной одинаковы, и

. (3.9)

Определим значение для некоторых частных случаев.

Передача двух дискретных сообщений видеоимпульсами с пассивной паузой, т.е. (рис. 3.2, а).

, (3.10)

где – удельная мощность помехи в полосе 1 Гц .

Как видно из (3.10), , а значит, и помехоустойчивость зависит только от энергии сигнала и не зависит от его формы. В частности, это означает, что передача «1» одиночным импульсом эквивалентна передаче кодовой группой, если энергия одного импульса равна энергии группы.

Передача двух дискретных сообщений радиоимпульсами с прямоугольной огибающей и пассивной паузой (рис. 3.2, б). В этом случае , а.

Подставляя в (3.6) и производя интегрирование, получим, что при

. (3.11)

Таким образом, заполнение видеоимпульса частотой не повышает его помехоустойчивость, а при той же амплитуде и длительности снижает её.

Рассмотрим теперь потенциальную помехоустойчивость передачи двух дискретных сообщений с активной паузой. Активная пауза означает, что если сигнал не посылается, то в линию поступает другой сигнал, отличный от нуля. Рассмотрим несколько случаев.

Частотная манипуляция. Передача осуществляется радиоимпульсами на разнесённых частотах и (рис. 3.2, в). Помехоустойчивость характеризуется величиной

При ,и, что имеет место в реальных условиях, получим

. (3.12)

При одинаковом динамическом диапазоне помехоустойчивость такой передачи эквивалентна помехоустойчивости при передаче видеоимпульсами с пассивной паузой (3.10).

Полярная манипуляция. Передача осуществляется разнополярными прямоугольными импульсами длительностью  (рис. 3.2, г), т.е. . Подставив значение в (3.6), получим

. (3.13)

Из сравнения выражений (3.10) и (3.13) следует, что помехоустойчивость при передаче разнополярными импульсами в два раза выше, чем при передаче видеоимпульсами с пассивной паузой.

Фазовая манипуляция. Передача осуществляется поочерёдно радиоимпульсами с одной и той же частотой, но с фазами, отличающимися на 180 (рис. 3.2, д), т.е. , а.

а

б

в

г

д

Рис. 3.2. Передача двух дискретных сообщений:

а – видеоимпульсами; б – радиоимпульсами; в – методом частотной манипуляции; г – с применением полярной манипуляции; д – с применением фазовой манипуляции

Подставляя в (3.6) и учитывая, что , получим

Сравнение выражений (3.10) и (3.14) показывает, что введение фазовой манипуляции приводит к улучшению помехоустойчивости.

Если сравнить дискретные методы манипуляции, то окажется, что самой помехоустойчивой является фазовая манипуляция.

Описанная помехоустойчивость элементарных сигналов предполагает наличие идеального приёмника, для реализации которого требуется знание фазы несущей частоты и амплитуды сигнала, а также наличие синхронизации начала приёма сигнала.