5.7. Фазовые модуляторы

Под фазовой модуляцией, как указывалось выше, понимается изменение фазы несущего колебания по закону изменения модулирующего напряжения. Эта задача может быть решена различными способами.

5.7.1. Фазовый модулятор с изменением расстройки колебательного контура. Схема подобного модулятора представлена на рис. 5.39.

Рис. 5.39. Фазовый модулятор с реактивным транзистором

Реактивный полевой транзистор VT1, с помощью которого осуществляется изменение резонансной частоты контура, включен параллельно контуру L1C4 усилителя, собранного на транзисторе VT2. Сигнал на усилитель подается от стабильного и независимого генератора с частотой ω1 через конденсатор связи С3. Конденсатор С1 и резистор R1 являются элементами реактивного полевого транзистора. Емкость С2 является блокировочной. Она представляет собой короткое замыкание для токов высокой частоты и очень большое сопротивления для модулирующего сигнала с частотой Ω.

Все сказанное о работе реактивного транзистора в подразд. 5.5.1 полностью остается применимым и к случаю фазового модулятора, лишь с той разницей, что изменение резонансной частоты контура приводит не к изменению частоты генерации, а к изменению фазы напряжения на контуре.

Связь между относительным изменением резонансной частоты контура / _P и фазовым изменением легко может быть представлена на основании выражения для фазовой характеристики контура.

Приравнивая  = θ, Р=1 и подставляя  = Дcost (где  Д – максимальное изменение частоты), получаем

Достоинство рассмотренного фазового модулятора – это возможность обеспечения высокой стабильности средней частоты путём применения кварцованного задающего генератора. Недостаток – малые значения θ max.

Получить θ max = (100 – 200)^о позволяют импульсно-фазовые модуляторы.

Экзаменационный билет № 18

АМ-АМ-сигналы. Для повышения помехоустойчивости иногда модулированное (АМ, ЧМ) сообщение дополнительно модулируют по частоте или амплитуде. Такой способ модуляции обозначается двумя индексами: пер- вый означает способ модуляции поднесущей, второй – несущей. Кроме того, двукратная модуляция применяется при передаче сообщений по радиоканалам, а также в выделенной полосе частот проводной линии связи.

АМ-АМ-сигналы в телемеханике используются редко. Однако их шумо-вые характеристики часто служат эталоном для сравнения различных методов модуляции. Рассмотрим АМ-АМ-сигнал, когда промодулированная по ампли- туде поднесущая описывается выражением

(4.17)

где Uω 1– амплитуда поднесущей; 1 – круговая частота поднесущей; m_AM – коэффициент амплитудной модуляции на первой ступени;  – круговая частота модулирующего сообщения. Сигнал U Н(t) является модулирующим по отношению к модулирующему колебанию.

В соответствии с определением амплитудной модуляции АМ-АМ-сигнал можно записать в виде

где M_AM = kU_ω1/U₀ – коэффициент амплитудной модуляции на второй ступени.

Процесс получения АМ-АМ-сигнала показан на рис. 4.9.

Для получения спектра преобразуем выражение (4.19) и окончательно получим

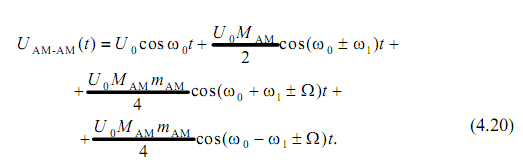
Согласно выражению (4.20) спектр АМ-АМ-сигнала имеет вид, представленный на рис. 4.10. Oн содержит составляющую на несущей частоте ₀, две боковые составляющие на частотах ₀_ и __, вокруг которых имеются по две составляющих на частотах __ и __ соответственно.

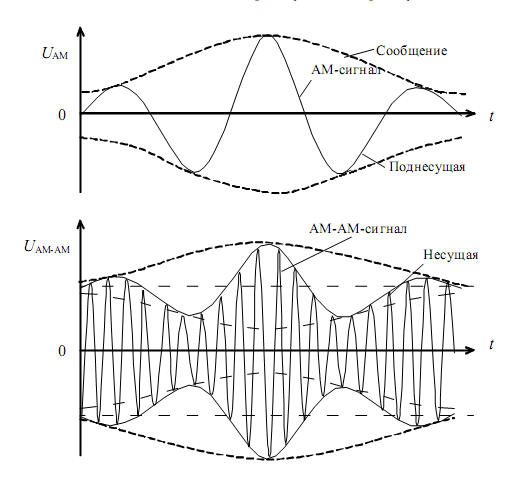
_{Рис. 4.9. Формы сигналов при АМ-АМ}

Рис. 4.10. Спектр АМ-АМ-сигнала

Очевидно, что необходимая полоса частот для передачи такого сигнала определяется разностьючастот верхней и нижней боковых составляющих, т. е.

_AM-AM ____2(_, (4.21)

2.2.7. Код с числом единиц, кратным трем. Этот код образуется добавлением к k информационным символам двух дополнительных контрольных символов (r=2), которые должны иметь такие значения, чтобы сумма единиц, посылаемых в линию кодовых комбинаций, была кратной трем. Примеры комбинаций такого кода представлены в табл. 2.5.

_{Таблица 2.5}

_{Код с числом единиц, кратным трем}

Он позволяет обнаружить все одиночные ошибки и любое четное количе- ство ошибок одного типа (например, только переход 0 в 1) не обнаруживаются двойные ошибки разных типов (смещения) и ошибки одного типа, кратные трем. На приемной стороне полученную комбинацию проверяют на кратность трем. При наличии такой кратности считают, что ошибок не было, два кон- трольных знака отбрасывают и записывают исходную комбинацию. Данный код обладает дополнительной возможностью обнаруживать ошибки: если первый контрольный символ равен нулю, то и второй тоже должен быть равен нулю.

2.2.8. Инверсный код (код с повторением инверсии). Это разновидность кода с двукратным повторением. При использовании данного кода комбинации с четным числом единиц повторяются в неизменном виде, а комбинации с не- четным числом единиц – в инвертированном.

Примеры представления кодовых комбинаций в инверсном коде приведе-

_{ны в табл. 2.6.}

_{Инверсный код}

Таблица 2.6

Прием инверсного кода осуществляется в два этапа. На первом этапе сум- мируются единицы в первой половине кодовой комбинации. Если их количест- во окажется четным, то вторая половина кодовой комбинации принимается без инверсии, а если нечетным – то с инверсией. На втором этапе обе зарегистри- рованные комбинации поэлементно сравниваются, и при обнаружении хотя бы одного несовпадения комбинация бракуется. Это поэлементное сравнение эк- вивалентно суммированию по модулю 2. При отсутствии ошибок в обеих группах символов их сумма равна нулю.

Рассмотрим процесс обнаружения ошибок наследующем примере. Пусть передана последняя кодовая комбинация из табл. 2.6. Ниже показано суммиро- вание для трех вариантов приема переданной комбинации:

В первом варианте принята комбинация 1110101110 10 . В первой половине кодового слова (информационных символах) четное количество единиц, поэтому производится ее суммирование по модулю 2 с неинвертируемыми кон- трольными символами r, что в результате дает нулевую сумму, т.е. комбина- ция принята без искажений.

Во втором варианте принята комбинация 1010101110 10 . Подсчитывая ко- личество единиц в информационных символах и замечая, что оно нечетное, контрольные символы инвертируют и суммируют с информационными симво- лами. Присутствие единиц в результате свидетельствует о наличии ошибки, ануль в этой сумме показывает ее место.

В третьем варианте принята комбинация 111010101010. Поскольку в ин- формационной последовательности четное количество единиц, при проверке контрольныесимволы суммируются с информационными без инверсии. В этом случае в итоге появляется одна единица. Ее место указывает номер искажен- ной позиции в принятой последовательности контрольных символов.

Таким образом, если при суммировании в результате среди единиц появ- ляется один нуль – ошибка появилась в первой половине принятой кодовой комбинации (в информационных символах) и нуль указывает ее место. Если в результате среди нулей появляется одна единица – ошибка во второй половине кодовой комбинации (в контрольных символах) и ее место указывает единица.Если в результате суммирования имеется несколько единиц или нулей, это оз- начает, что комбинация принята с несколькими искажениями.

Кодовое расстояние инверсного кода равно количеству разрядов исходного кода при k<4 и равно 4 при k>=4. Например, при d=4 код может обнаруживать двойные ошибки и исправлять одиночные. Обычно этот код используется только для обнаружения ошибок. Он позволяет обнаруживать ошибки любой кратности за исключением таких, когда искажены 2 информационных символа и соответствующие им 2 контрольных, 4 информационных и соответствующие им 4 контрольных и т.д.

Коэффициент избыточности инверсного кода равен 0,5.