1.6.4. Согласованный фильтр для финитного сигнала произвольной формы

Согласованный фильтр для финитного сигнала произвольной формы S(t) можно построить на основе неискажающей длинной линии, обеспечивающей задержку сигнала на время, с бесконечной плотностью отводов (рис. 1.13). Практически отводы можно брать в соответствии с теоремой отсчетов в дискретных точках с разносом t=0, 5/F, где F – эффективная ширина спектра сигнала.

Действительно, с помощью схемы, показанной на рис. 1.13, можно с хорошей точностью синтезировать любой сигнал S(t), представленный усеченным рядом Котельникова:

где; ; - ширина спектра сигнала. Такой сигнал можно получить на выходе идеального ФНЧ с полосой пропускания F, подавая на его вход последовательность - импульсов с весами через интервалы времени. Это осуществляется с известным приближением в схеме рис. 1.13. Если на вход А линии в начальный момент подается один короткий единичный импульс, аппроксимирующий - функцию, то с отводов снимаются такие же импульсы, разнесенные на интервалы , которые, пройдя через взвешивающие блоки , поступают поочередно на вход ФНЧ. Взвешивающие блоки содержат аттенюаторы или усилители с коэффициентом усиления, а также при отрицательных - инверторы.

Таким образом, схема рис.1.13 представляет собой линейный фильтр, называемый трансверсальным, с импульсной реакцией S(t). Легко видеть, что если входной импульс подать не в точку А., а в точку В, то будет синтезирован сигнал, представляющий зеркальное отображение S(t). Поэтому та же схема с входом в точке В. оказывается фильтром, согласованным S(t).

1.6.5. Согласованный фильтр для “пачки” знакопеременных импульсов

Предположим, что в качестве входного сигнала используется “пачка” из N знакопеременных прямоугольных видеоимпульсов длительностью каждый, длительность пачки равна Т (рис.1.14).

=

Синтез фильтра, согласованного с данным сигналом, осуществляется по тем же правилам, что и в предыдущем примере:

где,

Тогда:

где - частотный коэффициент передачи фильтра, согласованного с одиночным

прямоугольным видеоимпульсом, длительностью .

Схема фильтра, согласованного с сигналом, в виде “пачки” знакопеременных прямоугольных видеоимпульсов приведена на рис.1.15.

Векторная диаграмма напряжений данного согласованного фильтра при подаче на вход сигнала, с которым этот фильтр согласован, изображена на рис.1.16.

1.6.6. Согласованный фильтр для последовательности импульсов кода Баркера

Последовательностью Баркера называется последовательность из n импульсов прямоугольной формы, которые могут принимать значения +/-1, обладающая заданными автокорреляционными свойствами (при B(0)=1,).

Сигналы Баркера удается реализовать при числе позиций: 2,3,4,5,7,11 и 13. Последовательностью Баркера при n=11 и трансверсальный фильтр, согласованный с этим сигналом, синтезированный спектральным методом, показан на рис.1.17.

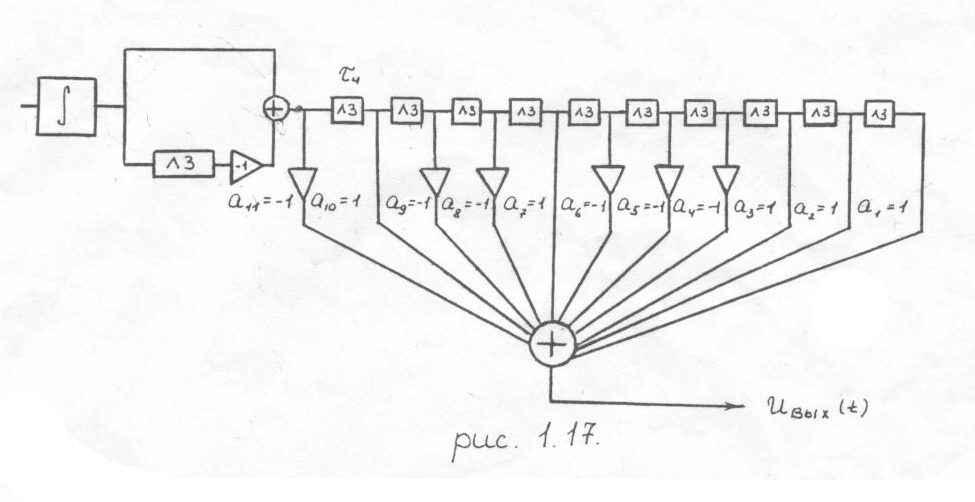
Ниже на рис.1.18 представлены диаграммы напряжений, поясняющие работу данного фильтра при подаче на его вход сигнала, с которым он согласован.

Напряжение на входе фильтра при этом совпадает по форме с автокорреляционной функцией сигнала, имеющей характерную Форму с (рис.1.18).