1.5. Оптимальная фильтрация сигнала, известного точно, при гауссовском “окрашенном” шуме

В отличии от выше рассмотренной задачи обнаружение сигнала известной формы производится на фоне шума с неравномерным энергетическим спектром (небелый, то есть окрашенный шум). Очевидно, что в данном случае передаточная функция фильтра должна быть согласованно не только со спектральной плотностью сигнала , но также с энергетическим спектром шума .

Наиболее простой способ отыскания требуемой передаточной функции заключается в приведении заданного шума к белому шуму. Для выяснения сути этого способа рассмотрим вспомогательную функциональную схему, показанную на рис. 1.6.

На этой схеме обозначает искомую передаточную функции синтезируемого фильтра, а и -передаточные функции двух вспомогательных, условных четырехполюсников, введение которого не оказывает никакого влияния на работу устройства, так как результирующая передаточная функция равна единице.

Так как функцию можно выбирать произвольно то модуль этой функции зададим в виде

где -постоянная величина.

Тогда на выходе первого четырехполюсника будет действовать шум с равномерным энергетическим спектром

, т.е. белый шум.

Само собой разумеется, сигнал на выходе этого четырехполюсника отличается от входного сигнала, так как спектральная плотность

отличается от .

Однако основной задачей является максимизация отношения сигнал/помеха на выходе всего устройства, поэтому важно отношение энергии сигнала к энергетическому спектру шума, а форма сигнала при этом роли не играет.

Так как в рассматриваемом сечении схемы шум является белым, то для получения на выходе максимума отношения сигнал/помеха вся последующая часть устройства должна иметь передаточную функцию, отвечающую условию (1.8). Таким образом, получаем:

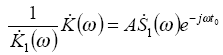
Левая часть этого выражения является результирующей передаточной функцией четырехполюсника, обведенного на рис.1.6 пунктиром, а правая часть – функция, комплексно-сопряженная по отношению к спектру, дополненная множителем .

Из выражения (1.29) следует

Тогда с учетом (1.28)

.

Таким образом,

Или окончательно, подставляя сюда соотношение (1.27),

Физический смысл этого соотношения в том, что и в случае белого шума, для максимизации отношения сигнал/шум в фильтре должна осуществляться компенсация начальных фаз спектра входного сигнала S(t). Поэтому в правую часть (1.31) входит комплексно-сопряженная функция. Однако модуль передаточной функции должен быть, во-первых, пропорционален модулю (как и в случае белого шума) и, во-вторых, обратно пропорционален энергетическому спектру шума на выходе фильтра. Тем самым обеспечивается подчеркивание тех компонентов спектра сигнала, при которых интенсивность шума меньше. Из окончательного результата (1.31) ясно, что задержка должна сопоставляться сигнала T на выходе фильтра.

1.6. Примеры реализации согласованных фильтров

1.6.1. Исходные положения

Основные выражения, определяющие передаточную и импульсную характеристики согласованного фильтра, дают возможность найти физическую структуру устройства для оптимальной фильтрации сигнала известной формы. Рассмотрим примеры такого синтеза.