Министерство образования Республики Беларусь

МИНСКИЙ РАДИОТЕХНИЧЕСКИЙ ИНСТИТУТ

Кафедра автоматической электросвязи

В.А. Овсянников, М.Ю. Хоменок

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

по курсу Теория передачи сигналов", часть I

Минск I982

УДК 621.395

АННОТАЦИЯ

Настоящий лабораторный практикум предназначен для студен­тов специальностей 0702 "Автоматическая электросвязь" и 0708 "Многоканальная электросвязь". В практикуме изложены методичес­кие указания по выполнению лабораторной работы № I "Синтез сиг­налов по дискретным отсчетам" по разделу "Системы связи и спосо­бы передачи сообщений" курса "Теория передачи сигналов".

- 55-01

Минский радиотехнический институт, 1982

Лабораторная работа №1

СИНТЕЗ СИГНАЛОВ ПО ДИСКРЕТНЫМ ОТСЧЕТАМ

Цель работы

Изучение метода синтеза сигналов по дискретным отсчетам в со­ответствии с теоремой Котельникова, исследование влияния частоты выборок и характеристик фильтров нижних частот на качество синте­зирования.

Краткие теоретические сведения

При передаче непрерывных сообщений по каналам связи с ис­пользованием импульсной модуляции или кодирования возникает не­обходимость дискретизации сообщений по времени. Сущность дискре­тизации заключается в том, что непрерывная во времени функция заменяется последовательностью коротких импульсов, амплитуды ко­торых равны значениям непрерывной функции в моменты появления им­пульсов. Эти значения непрерывной функции называют отсче­тами (выборками).

При этом частота дискретизации с целью наиболее точного представления непрерывного колебания в виде последовательности дискретных отсчетов должна быть определенным образом согласована с параметрами сигнала. Условия, при которых погрешность восста­новления непрерывной функции ƒ(t) no дискретным отсчетам бу­дет минимальной, определяются из прибавления непрерывной функции по системе ортогональных функций вида sin t/t.

1. Ряд котельникова

1.1. Обобщенный ряд Фурье

Функция ƒ(t), удовлетворяющая условию Дирихле и являющаяся квадратично интегрируемой в области определения т.е. , может быть представлена в виде ряда (1) по системе ортогональных, функций :

(1)

где C_n – коэффициенты Фурье.

Ряд (I) называется обобщенным рядом Фурье по данной системе ортогональных функций {}

(2)

Система функций (2) называется ортогональной на отрезке t€[a,b], если функции удовлетворяют условию

(3)

Величина

(4)

называется нормой функции. Коэффициенты Фурье определяются из условия ортогональности выбранной системы функций и вычисляются по формуле

(5)

Обобщенный ряд Фурье (I) обладает следующим важным свойством: при заданной системе ортогональных функций (2) и при фиксированном числе слагаемых ряда (1) он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратической ошибки) данной функции ƒ(t). Это означает, что среднеквадратическая ошибка, под которой подразумевается величина

(6)

достигает минимума, когда U_n=C_n.

1.2 Примеры систем ортогональных функций

1.2.1 Наиболее простой системой ортогональных функций, используемой при спектральном (гармоническом) анализе сигна­лов, является система тригонометрических функций

(7)

которые ортогональны на отрезке . Норма функций (7) равна Следовательно,

(8)

(9)

(10)

где

(11)

(12)

1.2.2 При использовании системы функций

(13)

ортогональных на отрезке , где тригонометрический ряд Фурье (10) будет определен в комплексной форме. Норма функций (13) равна=Т. Таким образом

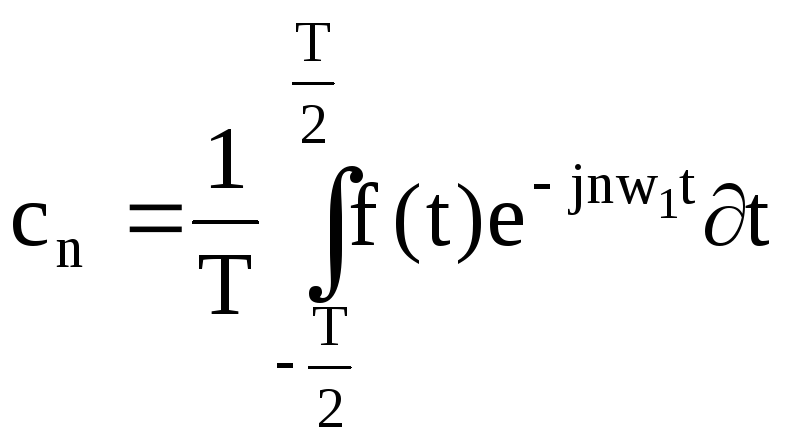(14)

1.2.3 Система функций вида

где n = 0,±1,±2,…, (15)

является ортогональной на бесконечном интервале -∞<t<∞. Норма функций, равна

(16)

функция обладает следующими свойствами:

а) в точке t=n∆t, ;

б) в точках t=m∆t, где m - любое целое число, от­личное от n,

в) спектральная плотность функции равномерна в полосе частот |w|<w_м и равна

Так как функция отличается от только сдви­гом на оси времени на величину n∆t то спектральная плотность функции равна

(17)

Графики функций и модуль спект­ральной плотности функции изображены на рис. 1.

Рис.1.

1.3. Ряд Котельникова

Рядом Котельникова называют разложение колебания ƒ(t), заданного на интервале -∞<t<∞ спектр которого огра­ничен максимальной частотой w_м, в ряд (1) по системе орто­гональных функций вида

Коэффициенты Фурье C_n определяются в соответствии с формулой (5) и равны

(18)

Пусть

(19)

(20)

тогда

(21)

где Ф_n*(jw) спектральная функция комплексно-сопряженная с Ф_n(jw). Соответственно

(22)

Таким образом, коэффициенты Фурье ряда (1) являются выборками функции ƒ(t) в точках t=n∆t. Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции ƒ(t), ряд

(23)

сходится к функций ƒ(t) при любом значении t. Выра­жение (23) называется рядом Котельникова и является основой дискретного представления сигналов.