7.2. Электрические цепи переменного тока

7.2.1. Однофазные цепи

При изучении цепей переменного тока необходимо обратить внимание на физические процессы, происходящие в цепях с индук­тивной и емкостной нагрузками.

В результате изучения данного раздела необходимо четко пони­мать смысл терминов: резистор, активное сопротивление, индуктив­ная катушка, индуктивность, индуктивное сопротивление, конденса­тор, емкость, емкостное сопротивление, полное сопротивление цепи, фаза, начальная фаза, угол сдвига фаз, период, частота, угловая часто­та, мгновенное, амплитудное и действующее значения токов и напря­жений, активная, реактивная и полная мощности цепи.

При исследовании процессов, возникающих в цепях синусои­дального тока, и особенно при расчете цепей приходится производить различные математические операции над синусоидами тока и напря­жения одной и той же частоты, но имеющими различные начальные фазы. Эти операции удобнее всего производить над действующими значениями, рассматривая их как векторы. При этом длины векторов в масштабе равны действующим значениям тока и напряжения, а на­чальная фаза определяет направление вектора относительно положи­тельной (обычно горизонтальной) оси координат. При положительной (опережающей) начальной фазе вектор повернут на соответствующий угол против часовой стрелки, а при отрицательной (отстающей) - по часовой стрелке.

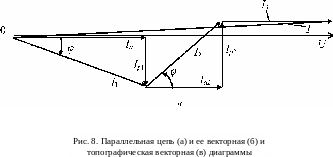
Совокупность нескольких векторов тока и напряжения, выходя­щих из общей точки, называют векторной диаграммой. Векторная ди­аграмма, на которой не все векторы выходят из общей точки, а конец какого-либо вектора является началом другого, называется топогра­фической диаграммой.

Для наглядности в некоторых случаях векторные топографиче­ские диаграммы объединяют в одну.

При помощи топографической векторной диаграммы удобно про­изводить сложение напряжений на отдельных участках последова­тельной цепи и сложение токов в ветвях параллельной цепи.

Топографическую диаграмму называют потенциальной диаграм­мой, так как каждая точка диаграммы соответствует определенной точке электрической цепи. Чтобы получить соответствие точек диа­граммы и цепи, потенциальная (топографическая) диаграмма строит­ся в той же последовательности, в какой происходит обход электри­ческой цепи. Ценность потенциальной диаграммы состоит в том, что она позволяет определить величину и фазу напряжения между любы­ми точками цепи. Для этого следует соединить соответствующие точ­ки потенциальной диаграммы отрезком прямой и придать этому от­резку соответствующее направление.

При построении векторных диаграмм один из векторов прини­мают за основной вектор. Обычно его располагают в положительном направлении по горизонтальной оси. В этом случае начальная фаза тока или напряжения, изображаемого данным вектором, равна нулю. Для последовательной цепи за основной вектор принимают вектор тока, а для параллельной - вектор напряжения.

В качестве примера на рис. 7 и 8 представлены одноконтурная и разветвленная электрические цепи и их векторные диаграммы.

В том случае, когда сложение или вычитание векторов требуется производить не графически, а математически (например, при расчете

электрической цепи), векторы раскладывают на две составляющие, одна из которой называется активной, а вторая - реактивной. Актив­ная составляющая напряжения совпадает на фазе с током, а реактив­ная - опережает ток или отстает от него по фазе на 90°. Зная угол сдвига по фазе между током и напряжением и величину тока и на­пряжения, легко определить соответствующие составляющие этих векторов.

U(u) -о о-

I

Ri U R2 C L2

-И*

Uui

■ж-

Ua2

■ж-

Uc

UL2

■ж-

U2

-*к-

U3

-и

a

Ul2=U

0

U2

б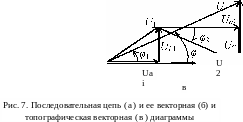

'KUu2=U
	Ui+U2>

Если задан синусоидально изменяющийся ток i=I_m-s\n(cot-(p), то действующие значения его активной и реактивной составляющих со­ответственно равны

I_a=Tcos(p; I_p=I-sm(p. (26)

Аналогично для напряжений:

U_a=Ucos(p; U_p=U-sm(p. (27)

В выражениях (26) и (27)

¹=&^U=72- ⁽²⁸⁾

На диаграммах, изображенных на рис. 7,в, 8,в, показаны активные и реактивные составляющие токов и напряжений.

Если необходимо произвести сложение двух или более векторов, выражающих собой токи или напряжения, определяют их активные и реактивные составляющие и модуль результирующего вектора:

I

^{V(Z /а Г + (S Il -SI с Г, (29)}

^{и = V(SUa)r+(sULrSU^)T, (30)}

где индексы L и C указывают на характер реактивной составляющей (индуктивный или емкостный).

Рассматривая электрические цепи переменного тока, необходимо обратить внимание на явления резонанса в цепях переменного тока. Изучая явления резонанса, следует усвоить следующее. При резонан­се напряжение и ток на зажимах цепи всегда совпадают на фазе. На­стройка цепи на резонанс зависит от схемы соединения индуктивного и емкостного элементов. Для последовательной цепи условием резо­нанса напряжений является равенство индуктивного и емкостного со­противлений

Xl=Xc. (31)

Для цепи, содержащей параллельный контур, в одну ветвь кото­рого включена катушка индуктивности, а в другую - конденсатор, ус­ловием резонанса токов является равенство проводимостей ветвей

bL=bc. (32)

При изучении резонанса в цепях переменного тока необходимо знать условия их возникновения, а также понимать практическое применение резонанса токов. В то же время следует понимать, что ре­зонанс в электрических устройствах может представлять опасность как для самих устройств, так и для обслуживающего персонала.

Для практических расчетов цепей переменного тока можно ис­пользовать метод комплексных чисел. Для расчета разветвленных це­пей переменного тока можно использовать также метод проводимо-стей.

При расчете методом комплексных чисел удобно выражать век­торы тока и напряжения, а также величину сопротивления и прово­димости комплексными числами, в которых активные составляющие

являются действительной частью, а реактивные составляющие -мнимой частью комплексного числа. Причем знак у мнимой части за­висит от характера реактивной составляющей. Знак «плюс» соответ­ствует индуктивному характеру реактивной составляющей, а знак «минус» - емкостному. Пример.

Рассчитать электрическую цепь (рис. 9), питаемую синусоидаль­ным напряжением.

Дано: £/=220 B; Я_г=3 Ом; R2=3 Ом; Li=10 мГн; £з=50 мГн; С2=400 мкФ; 7=50 Гц.

Определить токи I₁, I₂,1₃ в ветвях цепи, напряжения на участках цепи U_ab, U_bc, полную мощность S, активную мощность P, реактивную мощность Q. Построить векторную диаграмму.

R2 C2 1 n^z

Я.

Ri

_т I—i i II 1

* *з(!з)

U(u)

i1(I1)

Рис. 9. Электрическая цепь со смешанным соединением нагрузки

Решение задачи с использованием метода проводимостей.

1. Реактивные сопротивления каждой ветви:

^XC 2 -

Xli=2tt/Li=2-3,14-50-10-10^-3 = 3,14 Ом; 1 1

8 Ом;

2цЮ₂ 2 • 3,14 • 50 • 400 -10 "⁽

Хз=2тгДз=2-3Л4-50-50-10^-3=15,7 Ом. 2. Полные сопротивления ветвей (каждая ветвь представляет со­бой последовательное соединение элементов):

_V^R₃² ₊ ^X_L3 ^-

Z₁ -J R² + х\_х -43² + 3,14² - 4,34 Ом; Z₂ - д/R₂² + XC₂ -V3² + 8² - 8,5 Ом;

д/0² +15,7² -15,7Ом.

Z 3

3. Для определения величины сопротивления параллельного уча­стка воспользуемся проводимостями второй и третьей ветвей. Актив­ные и реактивные проводимости определяются по формулам

R . X

Z ² Z ² Активная проводимость второй ветви

g₂ = ^R2 = = — = 0,0414 См. ² Z₂² 8,5² 72,5

Реактивная проводимость второй ветви

b_{C 2} = ^X2 = _⁸_ = 0,1105 См. ^C2 Z₂² 72,5

Так как активное сопротивление в третьей ветви отсутствует, ак­тивная проводимость третьей ветви

g3 = 0.

Реактивная проводимость третьей ветви

b₃ = = = — = 0,06 См. ³ Z₃² 15,7² 15,7

Полная проводимость параллельного участка

_{У be =V (g2 + g3)}² _{+ (Ьз - b2 )}²

= д/ (0,0414 + 0)² + (0,0637 - 0,1105)² = 0,0622 См.

При сложении реактивных проводимостей емкостная проводи­мость по отношению к индуктивной берется с противоположным зна­ком.

4. Активное и реактивное сопротивления параллельного участка цепи:

_Rbc = ^gi_t = ^gl±^gL = Ш*. = 10,7 Ом;

e

0,0622²

X_bc = % = = ^{0,0637 - 0,}₂¹⁰⁵ = -12,1 Ом.

^{be yl 0,06222}

Так как в параллельном участке цепи преобладает емкостная про­водимость, сопротивление X_be получилось со знаком «минус».

В результате расчета сопротивлений R_be и X_be исходную схему можно представить в виде одноконтурной (рис. 10).

5. Эквивалентное сопротивление всей цепи

^Zэкв = V^(R1 + ^Rbe ⁾² + ^(XL1 ^{- X}be ⁾² =

= V (3 +10,7)² + (3,14 -12,1)² = 16,35 Ом.

о —I 1 *-H 1 ii

u(U)

₄ ii(Ii)

Рис. 10. Эквивалентная схема электрической цепи

6. Ток в первой ветви

U 220 I₁ = = = 13,45 А.

г_экв ^16,35

7. Напряжения на участках цепи

U_bc = I₁Z_bc = —— = —^,— = 218 В; ^{bc 1 bc} y_bc 0,0622

Uae=l1 Z1=13,45-4,34=58,4 В.

8. Токи в параллельных ветвях

= ^ = 218 = 25,7 а_;

² Z₂ 8,5

= ^ = 218 = 13,9 а.

³ Z₃ 15,7

9. Определим мощности. Полная мощность

S=U ^=220-13,45=2960 BA =2,96 кВА. Активная мощность

P=U I₁ cos <p=S cos ф, где ws<p = ^ = ^{R1+ Rbc} = -635 = 0,84.

^Zэкв ^Z^:e ^16,35

P=2960-0,84=2490 Вт=2,49 кВт.

Реактивная мощность

Q=U I₁ sin <^>=S sin ф,

X_экв — Xb_c 8,96 где svn^ = —^SKS- = —^T1 ^ = —— = 0,54.

"^^ЭКв "^^ЭКв ^16,35

Q=2960-0,54=1600 BAp=1,6 кВАр.

10. Построение векторной диаграммы (рис. 11) электрической цепи переменного тока со смешанным соединением удобно начинать с параллельного участка цепи. Приняв начальную фазу напряжения параллельного участка U_c равной нулю, определим углы сдвига фаз ф₂ и ф₃ между напряжением и токами I₂ и I₃:

= ^ = ^ = 0,353; ф2 = 69°20';

^Z 2 ^8,5

0

R3

0; ф3 = 90°.

Z3 15,7

Вектор тока I1 на векторной диаграмме находится как векторная сумма токов I2 и I3.

Далее по отношению к вектору тока I₁ откладываем вектор на­пряжения U_ab на последовательном участке. Так как нагрузка на этом участке активно-индуктивная, то вектор напряжения U_ab будет опере­жать вектор тока I1 на угол ф1.

Определим угол ф1.

cos ср₁

3

Z 4,34

0,692; ф₁ = 46° 15'.

^Uab

^ф2

I3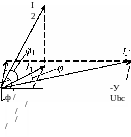

Рис. 11. Векторная диаграмма для электрической цепи со смешанным включением нагрузки

Вектор напряжения U является векторной суммой напряжений

Uab и Ubc.

U = Uab + Ubc .

Определим угол сдвига фаз ф между вектором U и током I1: cos^ = = J6³⁷- = 0,84; ф= 32°45'.

^Z ЭКВ ^16,35

Решение задачи методом комплексных чисел

1. Выразим сопротивления ветвей цепи в комплексной форме:

Z = R ± jX = ze^±J<P,

где z

_Vr ²_+x ²

X

p = arctg— R

Z₁ = R₁ + joL₁ = 3 + j 2n-50-10-10^-3 = 3 + j3,14 = 4,34e^{j 46} °¹⁵' Ом.

^Z 2 = ^R2 ^{- j}

1

3 - j

10⁶

2n-50 - 400

3 - j8 = 8,5e­

j 69° 20'

Ом.

Z₃ = joL₃ = j2n- 50 - 50 -10^-3 = j15,7 = 15,7e

j 90 °

Ом.

2. Выразим заданное напряжение U в комплексной форме. Если не задана начальная фаза напряжения, ее можно принять равной ну­лю. Направление вектора напряжения при этом совпадает с положи­тельным направлением действительной оси. Мнимая часть комплекс­ного числа в этом случае отсутствует (рис. 12): U = 220 В.

+j

U +

0

Рис. 12. Расположение вектора напряжения на комплексной плоскости

Ток в первой ветви

/1 ^U

_Z

экв

_Z ■ _{Z 85e}r^j69°²°'-_157e^j90°

где Z_me = Z + Z_bc = Z1 + = (3 + j314) + ^8be

Z₂ + Z₃ 3 - j8 + j15,7

1 1.1. S.J20°40'

= (3 + j314) +^133,5e₆₈°₅₀' = (3 + j3,14) + 16,2e^{- j 48}°¹⁰' = 8,3e^{j68 50}

= (3 + j'3,14) + (10,7 - j12,1) = 13,7 - j8,96 = 16,35e"^j32°⁴⁵' Ом.

I3

Таким образом,

220

j 32^o 45'

А.

= 13,45e

16,35e "^{j 32}°⁴⁵'

3. Для определения токов I₂ и I₃ найдем напряжение на парал­лельном участке U_bc:

U_bc = Z_bc ■ I₁ = 16,2e"^j48°¹⁰' ■ 13,45e^j32045' = 218e"^j15°²⁵ В,

218e "^j15025'

j 53⁰55'

25,7e

А,

_I = Ubc 2

^Z2 8,5e"^j6^²⁰'

218e -

j105^o25'

j15⁰25'

= 13,9e ^-

А.

_I = Ubc

3

^Z 3 15,7e^{j 90}°

4. Напряжение на последовательном участке ab

U_ab = I₁ ■ Z₁ = 13,45e^j32045' ■ 4,34e^j46°¹⁵' 58,4e^j790 В.

5. Выбрав масштаб по току и напряжению, по вычисленным зна­чениям строим векторную диаграмму токов и напряжений на ком­плексной плоскости (рис. 13).

6. Вычислим полную мощность

S = U ■ I₁ = 220-13,45e^{-j 32}°⁴⁵' = 2960e "^{j 32}°⁴⁵' ВА.

7. Для определения активной и реактивной мощностей кажущую- ся мощность, выраженную комплексным числом в показательной форме, переведем в алгебраическую форму. Тогда действительная часть комплексного числа будет являться активной мощностью, а мнимая - реактивной.

S=2960 cos 32°45'-j2960 sin 32°45'=2490-/1600 ВА. Откуда P=2490 Вт, Q=1600 ВАр.

8. Для проверки составляем баланс активных мощностей P = р + P₂ = I₁²R₁ + I₂²R₂ = 13,45² • 3 + 25,7² • 3 = 2490 Вт.