Нормальное распределение (Непрерывные случайные величины), часть теории №2
Из главы 3 вы уже узнаете, как можно определить, имеет ли некоторый набор данных приблизительно нормальное распределение. Теперь мы выясним, как вычислять вероятности для этого уже знакомого нам колоколообразного распределения. Одна из причин практической полезности использования нормального распределения состоит в том что, зная только среднее значение и стандартное отклонение, можно вычислить любую представляющую интерес вероятность (конечно, при условии, что распределение действительно нормальное).
Нормальное распределение — это непрерывное распределение, имеющее графическое представление в виде хорошо известной симметричной колоколообразной кривой, показанной на рис.7.3.1,а. Для любой комбинации значений среднего и положительного стандартного отклонения можно начертить свой график. Кривая сдвигается вправо или влево так, чтобы вершина “колокола” располагалась над средним значением, и растягивается или сжимается так, чтобы масштаб по горизонтали соответствовал стандартному отклонению. На рис. 7.3.1,б показаны два различных нормальных распределения.
Формула, описывающая нормальное распределение вероятности со средним значением µ и стандартным отклонением σ имеет вид:
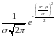
Представление вероятности как площади под кривой
Колоколообразная кривая позволяет наглядно представить вероятность для случая нормального распределения. Более правдоподобным оказывается наблюдение значений, расположенных вблизи центра кривой, там, где она подымается выше. Вблизи краев, где кривая проходит ниже, наблюдение соответствующих значений оказывается менее правдоподобным. Строго говоря, вероятность того, что значение попадет в некоторый интервал на числовой прямой, равна площади соответствующей области под кривой, как показано на рис. 7.3.2.
Обратите внимание на то, что заштрихованная область, расположенная вблизи центра кривой, имеет большую площадь, чем область такой же ширины, но расположенная ближе к краю. Для того чтобы увидеть это, сравните рис. 7.3.2 и 7.3.3.
Рис. 7.3.2. Вероятность того, что имеющая нормальное распределение случайная величина принимает значения, лежащие в некотором интервале, равна площади под кривой нормального распределения между значениями, ограничивающими этот интервал. Вероятность наблюдения тех значений, которые ближе расположены к среднему, оказывается выше
Стандартное нормальное распределение z и соответствующие вероятности
Стандартное нормальное распределение — это нормальное распределение со средним значением µ = 0 и стандартным отклонением σ = 1. Соответствующая формула имеет вид:
f(x)
=
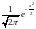
Для обозначения случайной величины, имеющей стандартное нормальное распределение, часто используют букву Z. Один из способов вычисления вероятностей для нормального распределения состоит в использовании таблиц вероятностей для стандартного распределения, поскольку совершенно нереально заготовить таблицы для каждой возможной комбинации среднего и стандартного отклонения. С помощью стандартного нормального распределения можно представить любое нормальное распределение, если рассмотрение вести не в реальных единицах измерения (например, в долларах), а в количествах стандартных отклонений в большую или меньшую сторону от среднего. Стандартное нормальное распределение показано на рис. 7.3.4.
Таблица вероятностей для стандартного нормального распределения (табл. 7.3.1) содержит вероятности того, что имеющая стандартное нормальное распределение случайная величина Z принимает значение меньше некоторого заданного числа z. Например, вероятность того, что величина Z меньше 1,38, равна 0,9162; это проиллюстрировано площадью под кривой распределения на рис. 7.3.5.
Табл. 7.3.1. (фрагмент)
z |
p |
z |
p |
z |
p |
z |
p |
z |
p |
z |
p |
-2,00 -2,01 … -2,38 … -3,00 |
0,0228 0,0222 … 0,0087 … 0,0013 |
-1,00 -1,01 … -1,38 … -2,00 |
0,1587 0,1562 … 0,0838 … 0,0228 |
-0,00 -0,01 … -0,38 … -1,00 |
0,5 0,4960 … 0,3520 … 0,1587 |
0,00 0,01 … 0,38 … 1,00 |
0,5 0,5040 … 0,6480 … 0,8413 |
1,00 1,01 … 1,38 … 2,00 |
0,8413 0,8438 … 0,9162 … 0,9772 |
2,00 2,01 … 2,38 … 3,00 |
0,9772 0,9778 … 0,9913 … 0,9987 |
Действительно, видно, что заштриховано около 90% всей площади под кривой. Для того чтобы найти точное значение (0,9162), в таблице вероятностей для стандартного нормального распределения необходимо найти z = 1,38 и посмотреть, какая вероятность соответствует этому значению. Найдите также строки для значений 2,35 (соответствующая вероятность 0,9906), 0 (соответствующая вероятность 0,5000) и -082 (соответствующая вероятность 0,2161). А какая вероятность соответствует значению z = 0,36?
