Лабораторное занятие 9

Тема: Получение первоначального опорного плана в транспортных задачах

Время 4 часа

Вопросы для контроля:

1. Подклассом, какого класса задач являются транспортные задачи?

2. В чем заключаются особенности транспортных задач как задач линейного программирования?

3. Сколько базисных переменных должно быть в первоначальном опорном плане?

4. Какие методы существуют для получения первоначального опорного плана?

5. Какое название имеет симплекс-метод для транспортных задач?

6. В чем заключается существо метода «северо-западного угла»? В чем его достоинства и недостатки?

7. В чем заключается существо метода «наименьших затрат»? В чем его достоинства и недостатки?

8. В чем заключается существо метода Фогеля? В чем его достоинства и недостатки?

9. Какая транспортная задача называется закрытой, открытой?

10. В чем заключается существо приема используемого для получения первоначального опорного плана в особых случаях?

1. Теоретическая часть

1.1 Экономико-математическая модель транспортной задачи

Важным частным случаем задачи линейного программирова­ния является, так называемая, транспортная задача. Покажем постановку такой задачи на конкретном примере.

Задача 13.1. Построить экономико-математическую модель следующей задачи. Имеются три поставщика А₁, А₂, А3 и четыре потребителя В₁,В₂,В₃,В₄ . Возможности поставщиков и спросы потребителей, а также затраты на перевозку единицы груза для каждой пары «поставщик – потребитель» сведены в таблицу поставок (таблица 13.1).

Таблица 13.1- Исходные данные к задаче 13.1

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4
		20	110	40	110
1	60	1 x11	2 x12	5 x13	3 x14
2	120 x21	1 x21	6 x22	5 x23	2 x24
3	100	6 x31	3 x32	7 x33	4 x34

В левом верхнем углу произвольной (i,j) -клетки (i - номер строки, j - номер столбца) записывается, так называемый, коэффициент затрат - затраты на перевозку единицы груза от i-гo поставщика к j-мy потребителю, Например, в левом верхнем углу клетки (1,4) записано число 3, следовательно, перевозка единицы груза от l-ro поставщика к 4-му потребителю обойдется в 3 условных денеж­ных единицы и т. д.

Задача ставится следующим образом.

Вычислить объемы перевозок для каждой пары «поставщик – потребитель» (x_ij) так, чтобы:

1) мощности всех поставщиков были реализованы;

2) спросы всех потребителей были удовлетворены;

З) суммарные затраты на перевозку были бы минимальны.

Решение. Построим математическую модель данной задачи.

Вычисляемый объем перевозки от i-ro поставщика к j-мy потребителю обозначим через x_ij и назовем поставкой клетки (i,j). Например, x_I2 - вычисляемый объем перевозки от 1­ - го поставщика ко 2-му потребителю или поставка клетки (1,2) и т. д.

Заданные возможности поставщиков и спросы потребите­лей накладывают ограничения на значения вычисляемых неизвестных x_ij. Так; например, объем груза, забираемого от l-го поставщика, должен быть равен мощности этого поставщика - 60 едини­цам, т.е. x₁₁ + x_I2 + x_I3 + x₁₄ = 60 (уравнение баланса по пер­вой строке).

Таким образом, чтобы мощность каждого из по­ставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок, которые составят систему линейных ограничений – равенств по мощностям:.

x₁₁ + x_I2 + x₁₃ + x_I4 = 60,

x₂₁ + x₂₂ + x_2З + x₂₄ = 120,

x_3I + x₃₂ + x₃₃ + x₃₄ = 100. (13.1)

Аналогично, чтобы спрос каждого из потребителей был удов­летворен, подобные уравнения баланса составляем для каждого столбца таблицы поставок. Они составят систему линейных ограничений –равенств по потребностям: ­

x₁₁ + x₂₁ + x_ЗI= 20,

x_I2 + x₂₂ + x_З2 = 110,

x₁₃ + x_2З + x₃₃ = 40,

. x_I4 + x₂₄ + x_З4 = 110. (13.2)

Очевидно, что объем перевозимого груза не может быть отри­цательным, поэтому следует дополнительно предположить, что

x_ij ≥ 0 (i= 1,2,3; j= 1,2,3,4). (13.3)

Суммарные затраты F на перевозку выражаются через коэффициенты затрат и поставки, образуя линейную форму:

F =1x₁₁ +2x₁₂ + 5x₁₃ + 3x₁₄ + 1x₂₁ + 6x₂₂ + 5x_2З + 2x₂₄ + 6x_З1 + 3x_З2 + 7x₃₃ + 4x_З4

(13.4 )

Теперь можно дать математическую формулировку задачи (без обращения к ее содержательному смыслу). На множестве неотрuцательных решений систем ограничений (13.1) и (13.2) получить такое решение Х* = (x*₁₁, x*₁₂, ..., x*₃₃, x*_З4) , при котором линейная функция (13.4) принимает минимальное значение.

Особенности математической модели транс­портной задачи: .

- системы ограничений есть системы - уравнений (т.е. транспорт­ная задача задана в канонической форме); .

- коэффициенты при переменных системы ограничений равны единице или нулю;

- каждая переменная входит в систему ограничений два раза: один раз - в систему (13.1) и один раз - в систему'(13.2).

Для математической формулировки транспортной задачи в общей постановке обозначим через c_ij коэффициенты затрат, че­рез М_i; - мощности поставщиков, через N_j - мощности потре­бителей, где i = 1,2, ..., т; j = 1,2, ..., п; т - число поставщиков, п - число потребителей.

Тогда система ограничений примет вид

, (13.5 )

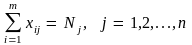. (13.6 )

Система (13.5) включает в себя уравнение баланса по строкам, а система (13.6) - по столбцам таблицы поставок. Линейная функ­ция в данном случае

. (13.7)

Математическая формулировка транспортной задачи в общей постановке будет следующей: на множестве неотрицательных (допустимых) решений системы ограничений (13.5), (13.6) вычислить такое решение

X* = (x*₁₁, x*₁₂, ..., x*_ij, …, x*_mn) , при котором значение линейной функции (13.7) минимально.

Произвольное допустимое решение X =(x₁₁, x₁₂, ..., x_ij, …, x_mn) системы ограничений (13.5), (13.6) назовем распределением поставок. Такое решение задает заполнение таблицы поставок, поэтому в дальнейшем значение произвольной переменной x_ij и содержимое соответствующей клетки таблицы поставок будут отождествляться.

Транспортная задача, приведенная в данном примере, обладает. важной особенностью: суммарная мощность поставщиков равна суммарной мощности потребителей, т.е.

. ( 13.8 )

Такие транспортные задачи называются закрытыми (говорят также, что транспортная задача в этом случае имеет закрытую модель). В противном случае транспортная задача называется открытой (открытая модель транспортной задачи).

Рассмотрим закрытую транспортную задачу. Являясь зада­чей линейного программирования, транспортная задача может быть решена симплексным методом. Однако специфичная форма системы ограничений данной задачи позволяет сущест­венно упростить обычный симплексный метод.

Модификация симплексного метода применительно к транспортной задаче называется распределительным методом. По аналогии с общим случаем решение в нем осуществляется по шагам, и каждому шагу соответствует разбиение переменных на основные (базисные) и неосновные (свободные).

Число r основных переменных транспортной задачи равно рангу системы линейных уравнений (максимальному числу ли­нейно независимых уравнений в системе ограничений).

Теорема 131. Ранг r системы уравнений (13.5, 13.6) при условии (13.8) равен т+п -1.

Прежде всего заметим, что уравнения системы (13.5, 13.6) при условии (13.8) линейно зависимы и, следовательно, ранг системы, не больше, чем m + n - 1.

Действительно, сравним сумму

(13.9 )

первых т уравнений системы (сумму уравнений системы (13.5) с суммой

( 13.10 )

оставшихся п уравнений (суммой уравнений системы (13.6).

Согласно условию (13.8) правые части уравнений (13,9,13.10) совпадают. Левые части (13,9,13.10), являющиеся суммами все­возможных переменных x_ij данной задачи, также совпадают. Сле­довательно, совпадают уравнения (13,9,13.10), т.е. сумма первых т уравнений системы ограничений равна сумме оставшихся п уравнений системы ограничений: уравнения системы (13,9,13.10), линейно зависимы.

Докажем, что ранг r системы не меньше, чем т+п-1. Из ли­нейной алгебры известно, что если некоторые k переменных про­извольной системы линейных уравнений можно линейно выра­зить через остальные переменные системы, то ранг этой системы не меньше, чем k.

Выразим, например, переменные x_ij, входящие в первый стол­бец и первую строку таблицы 13.1, через остальные переменные x_ij, где i = 2, 3, ..., т, j = 2, 3,. ..., п. Сначала получим такие выражения для переменных, отличных от х₁₁.

Для каждой переменной х_lj первой строки, где j = 2, 3, ..., п, воспользуемся уравнением ба­ланса по соответствующему столбцу:

( 13.11 )

Аналогично для каждой переменной Х_i1 первого столбца, где i = 2, 3, ..., т, воспользуемся уравнением баланса по соответствующей строке:

(13.12)

Для получения выражения для х₁₁ воспользуемся, например, уравнением баланса по первой строке:

( 13.3 )

Подставляя в правую часть уравнения (13.3) выражения для х_lj, где j = 2, 3, ..., п из уравнения (13.2), получаем выражение для x_ll.

Таким образом, т+п- 1 переменных этой задачи можно вы­разить через остальные тп-т-п+l переменные, т.е. ранг r системы r ≥ т + п - 1.

Сравнивая два полученных ограничения на ранг r системы (13.9,13.10

(r ≥ т+п-l и r ≤ т+п-l), получаем, что r = m+п - 1.

Основное следствие теоремы 13.1 - число r основных (базисных) переменных закрытой транспортной задачи равно т+п–1, где т ­ число поставщиков, п - число потребителей.

Каждому разбиению переменных х_ij задачи на основные (базисные) и неосновные (свободные) соответствует базисное решение и, как следствие, заполнение таблицы поставок, которое также назовем базисным.

Иными словами, распределение поставок называется базисным, если пepеменные, соответствующие заполненным клет­кам, можно принять за основные переменные. Клетки, отвечающие базисным переменным, в дальнейшем будем называть базисны­ми, а клетки, соответствующие.- свободным переменным, - сво­бодными или пустыми. Поскольку в дальнейшем мы используем исключительно базисные распределения поставок, то термины «базисная клетка» и «заполненная клетка» будем считать равнозначными.

Подобно тому, как это было в симплексном методе, в рас­пределительном методе решения транспортной задачи будем переходить от одного базисного распределения поставок к дру­гому в сторону невозрастания целевой функции вплоть до опти­мального решения. Для начала такого движения потребуется исходное базисное распределение поставок - так называемый опорный план.