Шпора по ТВиМС

1. Теорема сложения:

­– для 2-х зависимых событий ­– для 3-х зависимых с.

­– для n зависимых событий

– для n независимых событий

2. Теорема умножения:

­– для 2-х зависимых событий – для n зависимых событий

– для n независимых событий

3. Комбинаторные формулы (размещения и сочетания):

– число размещений с повторением элементов (k из n)

– число размещений без повторения элементов (k из n)

– число сочетаний без повторения элементов (k из n)

4. Формула полной вероятности:

A – событие – одна из гипотез

4. Формула Байеса:

– вероятность того, что событие произошло совместно с i-й гипотезой

4. Формула Бернулли: вероятность того, что событие A появится ровно в k опытах из n возможных равна:

4. Формула Пуассона (при 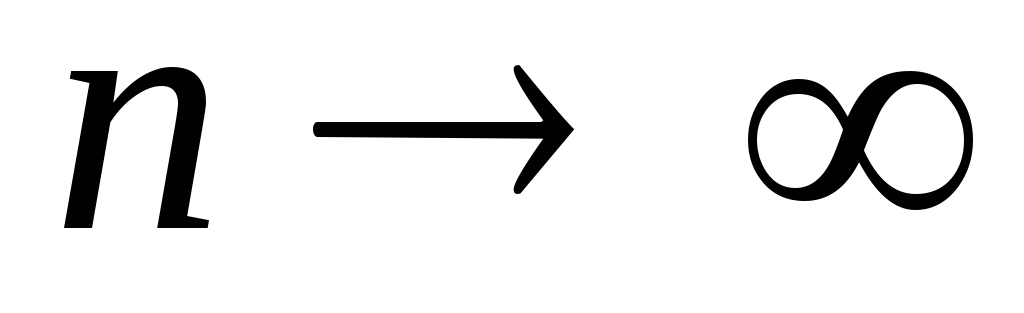, а вероятность события A в одном опыте так, что существует предел , ):

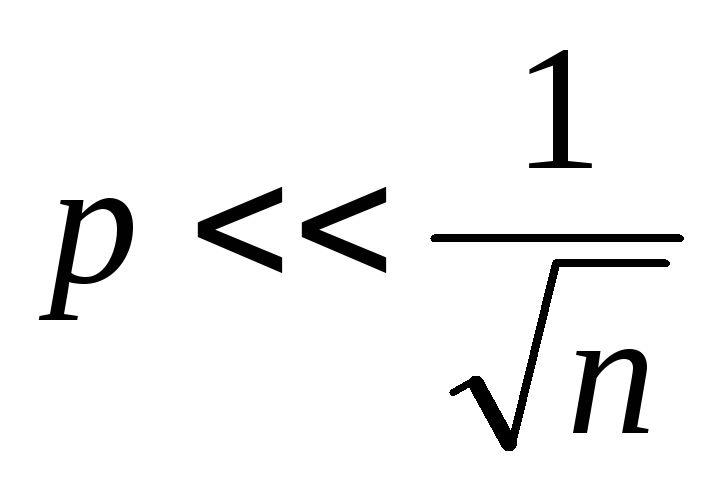
5. Локальная формула Муавра-Лапласса (число опытов достаточно велико, вероятность p не мала, и выполняются условия: ):

6. Интегральная формула Муавра-Лапласса(вероятность поподания k в интервал ):

7. Функция распределения: Свойства:

1. Диапозон значений:

2. 

3. 

4. – неубывающая:

5. Вероятность попадания в произвольный интервал:

11. Ряд распределения: это таблица значений и соответствующих м вероятностей:

    		...		– переход к функции распределения
    		...

12. Плотность распределения: 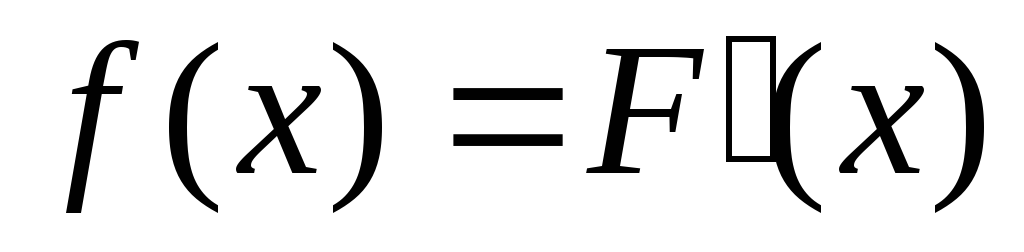Свойства:

1. 

2. Вероятность попадания в произвольный интервал:

3. Условие нормировки:

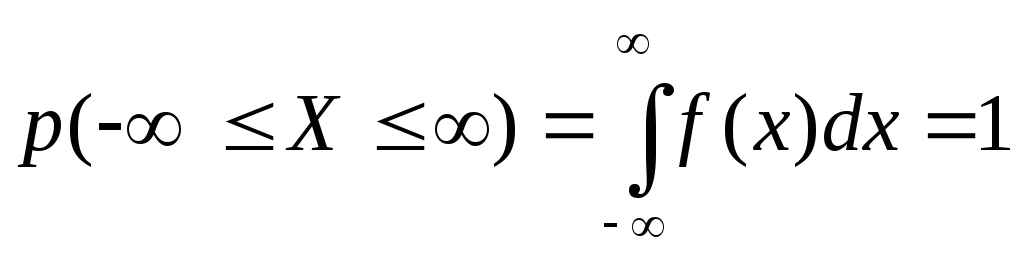
4. Переход к функции распределения:

11. Числовые характеристики случайнах величин:

1. Математическое ожидание ― эл-ты ряда распределения, ―плотность распределения.

Свойства: 1. 2. 3.

2. Начальный момент

3. Центрированные величины: (Мат. Ожидание находится в начале коорд.)

4. Центральный момент k-го порядка:

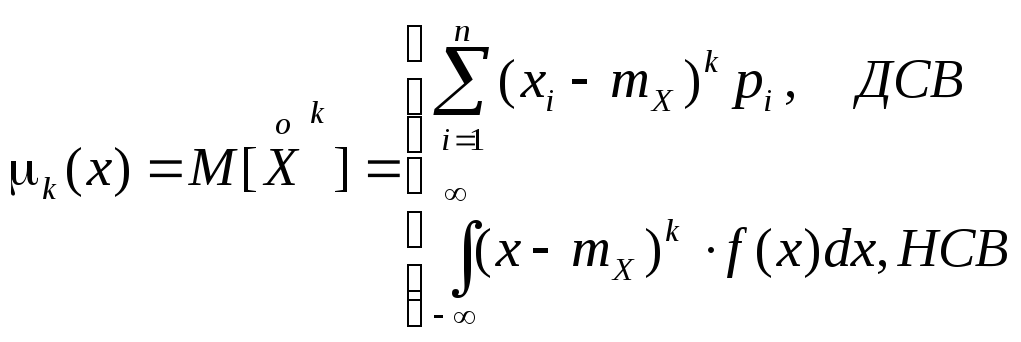
5. Дисперсия(среднее квадратичное отклонение): Свойства: 1. 2. 3. 4.

6. Мода (Mo) ― наиболее вероятное значение f(x):