2.1 Расчет геометрических размеров

Найдем длину волны ультразвукового поля в светозвукопроводе:

где υ_ак – скорость распространения акустической волны в СвЗвПр.

Определим угол падения оптического луча на модулятор:

По условию дифракции Брэгга, параметр дифракции на несущей частоте f₀, Q₀ должен быть намного больше 1:

Отсюда находим l – длину пути оптического луча в ультразвуковом поле:

Если выбрать l < 1,5мм, то эффективность дифракции будет очень маленькой. С другой стороны при l > 7 мм появляется дополнительная неоднородность ультразвукового поля из-за естественной расходимости светового пучка. Учитывая эти условия, выбираем l = 2 мм.

Выбрав оптимальную длину, вновь определяем диапазон акустических частот (он не должен сильно отличаться от заданного):

Найдем ширину оптического луча, взаимодействующего со звуковой волной, h:

ПП представляет собой резонатор, поэтому выбираем толщину его, равную половине длины волны возбуждаемого им ультразвукового поля:

Размеры СвЗвПр выбираем исходя из размеров ПП.

Длину СвЗвПр выбираем равную длине ПП:

a = l = 2 мм

Ширина СвЗвПр должна быть больше чем ширина ПП, с > h. Выбираем c = 2 мм.

Высота СвЗвПр должна быть больше ширины входного светового пучка, b > D_ВХ.

Чтобы определить D_ВХ, необходимо найти минимальное число разрешимых элементов по частоте, δf_min:

где N – число элементов ПЗС.

Выберем в качестве ПЗС К1200ЦЛ7 со следующими параметрами:

– число элементов 1024×1;

– размер элементов 13×500 мкм.

Получаем:

где δf выбирается в пределах (3÷7)δf_min.

Выберем δf = 6δf_min = 3·0,03 = 0,18 МГц.

Тогда высоту СвЗвПр выбираем b = 5 мм.

2.2 Расчет электрических параметров

Электрические параметры рассчитаны в п.1.2.

2.3 Расчет функциональных параметров

D_ВХ и δf_min были определены в п.2.1. Необходимо определить фокусное расстояние линзы, обеспечивающей преобразование Фурье модулированного сигнала. Для этого определим максимальное и минимальное отклонение максимума в задней фокальной плоскости линзы от центральной оси:

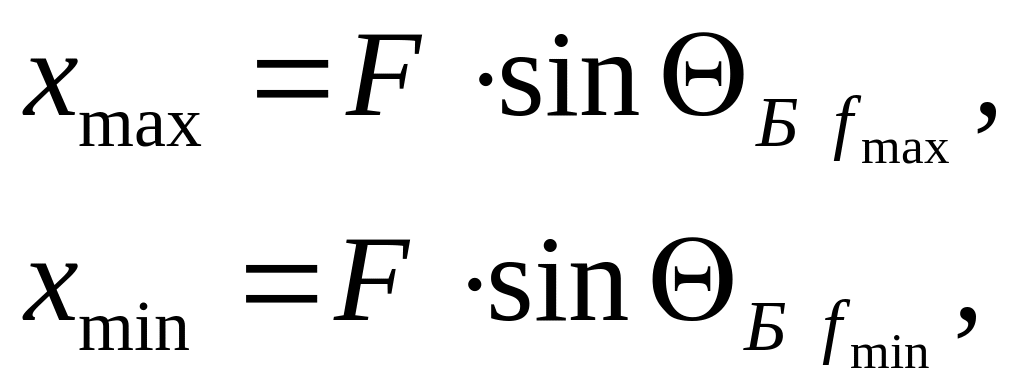
где – синус угла падения оптического луча при максимальной и минимальной частоте, f_max и f_min ультразвукового сигнала.

Разность x_max–x_min примем как размер элемента ПЗС, т.е.

Отсюда находим F:

2.4 Расчет основных параметров и характеристик аоас

Естественная расходимость пучка:

Общий диапазон сканирования:

Акустооптическое сопротивление пьезопреобразователя:

Акустооптическое сопротивление активной среды

Относительная ширина полосы частот

Одним из важных параметров АОАС является динамический диапазон,

определяющий диапазон входной мощности, при котором характеристики АОМ остаются неизменными.

где P_{ЭЛ min} определяется чувствительностью фотодетектора, P_{ЭЛ min} = 1 мкВт;

P_{ЭЛ.ТРЕБ} определяется через P_AK.ТРЕБ.

P_AK.ТРЕБ в свою очередь выбирается на половине линейного участка графика функции эффективности дифракции, η(P_AK):

где

Рисунок 2.2 – График зависимости эффективности дифракции от P_AK

По заданию η_d0 = 70%, при этом P_AK.ТРЕБ = 19,6 мВт.

Находим P_{ЭЛ.ТРЕБ}:

где α_общ – потери в среде и на границе раздела сред ПП и СвЗвПр.

Общие потери потока звуковой энергии (α_общ), в модуляторе, будут складываться из потерь в активной среде, потерь на границе преобразователь– активная среда и потерь в преобразователе, т.е.

где α_акср – акустические потери в средней точке базы звукопровода;

α_гр – акустические потери на границе преобразователь – звукопровод;

α_п – акустические потери в пьезопреобразователе.

где τ_ак – коэффициент пропускания границы преобразователь – звукопровод.

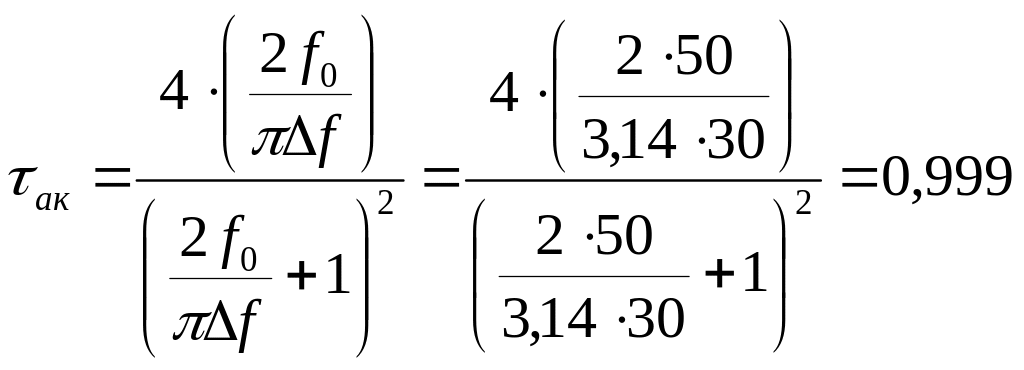
Акустические потери в пьезопреобразователе, с учетом толщены пьезопластинки:

где α – коэффициент оптического поглощения.

Так как акустические потери в пьезопреобразователе очень малы то не будем их учитывать, тогда общие потери потока звуковой энергии в модуляторе:

.

Тогда:

Минимальное число разрешимых элементов по частоте δf было определено в п.2.1.

Быстродействие АОАС определяется временем максимального и минимального взаимодействия τ_max, τ_min: