Задачи для самостоятельного решения
1. Имеются следующие данные о размере семьи работников цеха (число человек в семье):
3; 4; 5; 2; 3; 6; 4; 2; 5; 3; 4; 2; 7; 3; 3; 6; 2; 3; 8; 5; 6; 7; 3; 4; 5; 4; 3; 3; 4; 2.
Требуется:
1) составить дискретный вариационный ряд;
2) составить ряд распределения частот;
3) дать графическое изображение ряда в виде полигона частот;
4) определить средний размер семьи работников цеха, моду и медиану.
2. Ежедневные суммарные денежные вклады населения (в тыс. рублей) в отделение банка в течение последних 20 рабочих дней были таковы: 60; 20; 70; 70; 30; 20; 50; 40; 50; 60; 30; 40; 30; 50; 50; 60; 50; 60; 40; 40.
Требуется:
1) составить дискретный вариационный ряд;
2) составить ряд распределения частот;
3) дать графическое изображение ряда в виде полигона относительных частот;
4) определить моду и медиану.
3. Имеются следующие данные о распределении продовольственных магазинов региона по размеру товарооборота в млн. рублей:
Группа магазинов по товарообооту (млн. руб.), |
40-50 |
50-60 |
60-70 |
70-80 |
80-90 |
90-100 |
Число магазинов, |
2 |
4 |
7 |
10 |
8 |
7 |
Требуется:
1) дать графическое изображение ряда в виде гистограммы, полигона, кумуляты частот;
2) определить средний товарооборот магазинов, моду и медиану.
4. Представлен интервальный ряд распределения рабочих цеха по возрасту (лет):
Группа рабочих по возрасту (лет), |
18-21 |
21-24 |
24-27 |
27-30 |
30-33 |
33-36 |
36-39 |
Число рабочих, |
1 |
3 |
6 |
10 |
5 |
3 |
2 |
Требуется:
1) дать графическое изображение ряда в виде полигона, гистограммы относительных частот;
2) Определить средний возраст рабочих цеха, моду и медиану.
4.4. Показатели асимметрии и эксцесса
Показатель асимметрии и показатель эксцесса являются показателями формы распределения.
Пример 17.1. По приведенному выше примеру: даны тарифные разряды 25 рабочих цеха:
4; 3; 6; 4; 4; 2; 3; 5; 4; 4; 5; 2; 3; 4; 4; 5; 2; 3; 6; 5; 4; 2; 4; 3; 5 определить показатель асимметрии и показатель эксцесса.
Решение:
Показатель асимметрии учитывает асимметрию в распределении и вычисляется по формуле:
,
Где
- среднее квадратичное отклонение,
определяется по формуле:
,
(тар.
разряд)2
.
Асимметрия левосторонняя незначительная.
Существует
другая формула для расчета
:
;
-
центральный момент третьего порядка
оценка степени существенности этого
показателя As
дается с помощью средней квадратической
ошибки
.
,
,
Где n – число наблюдений.
Если
, то асимметрия не существенна. Принимается
гипотеза о нормальном распределении.
Для симметричных распределений рассчитывается показатель эксцесса:
-
центральный момент четвертого порядка.
,
,
.
имеет
знак ( - ). Это значит низковершинное
распределение.
Средняя квадратическая ошибка эксцесса высчитывается по формуле:
.
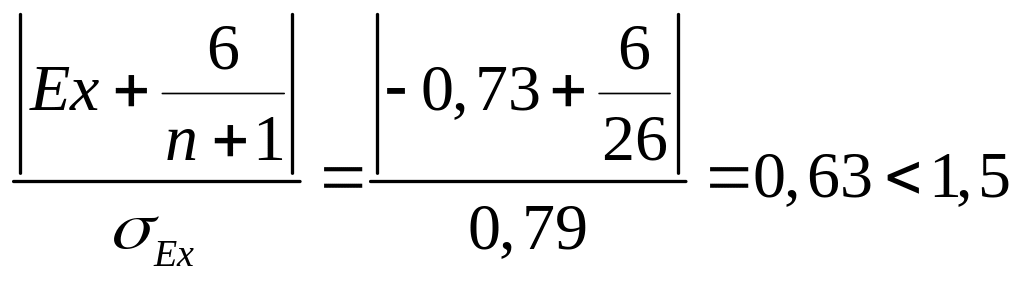
Т.к. оба показателя < 1,5 , то гипотеза о нормальном распределении не отвергается.
Пример 17.2. Дан интервальный ряд распределения студентов вечернего отделения по возрасту:
Группы студентов по возрасту (лет), |
18-22 |
22-26 |
26-30 |
30-34 |
34-38 |
Число студентов, |
2 |
7 |
11 |
6 |
4 |
лет
лет
Определить показатели асимметрии и эксцесса.
Решение:
Показатель асимметрии:
.
(лет).
.
Асимметрия правосторонняя незначительная.
.
Асимметрия несущественна.
.
.
.
Знак ( + ) – островершинное распределение.
.
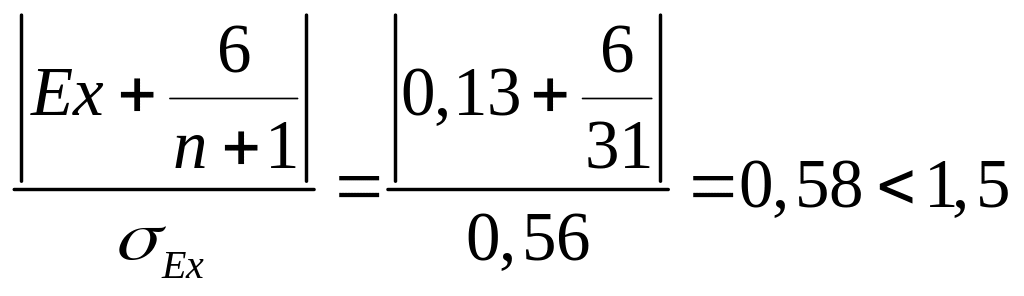
Т.к. оба показателя < 1,5 , то не отвергается гипотеза о нормальном распределении.