Задачи для самостоятельного решения

1. Имеются данные о времени простоя автомобиля под разгрузкой в (мин):

12; 10; 8; 15; 19; 12; 8; 10; 18; 8; 20; 20; 10; 12; 10.

Требуется: 1) составить вариационный ряд; 2) найти моду и медиану.

2. По результатам наблюдений: 1; 7; 7; 2; 3; 2; 5; 5; 4; 6; 3; 4; 3; 5; 6; 6; 5; 5; 4; 4 построить вариационный ряд, найти моду и медиану.

3. Имеются следующие данные о количестве заявок на автомобили технической помощи по дням в (шт.): 12; 2; 5; 14; 7; 2; 8; 10; 2; 6; 10; 8; 3; 13; 11; 8; 8; 2; 9; 8; 5; 14; 4; 10; 12; 6; 8; 2; 8; 7.

Требуется: 1) составить интервальный ряд распределения;

2) найти моду и медиану.

4.2. Эмпирическая функция распределения

Пример 15.1. По десяти наблюдениям над случайной величиной получена выборка: 5; 4; 4; 7; 6; 4; 5; 4; 6; 5. Построить: 1) вариационный ряд; 2) ряд распределения частот и эмпирическую функцию распределения.

Решение.

1) Вариационный ряд будет иметь вид: 4; 4; 4; 4; 5; 5; 5; 6; 6; 7.

2) Ряд распределения частот – таблица. В ее верхней строке- значение признака (варианта), в нижней строке частота варианты .

	4	5	6	7
	4	3	2	1

3) По ряду распределения частот строим эмпирическую функцию распределения: , где m_x – число вариант меньших х, n- объем выборки. Объем выборки: .

Найдем искомую эмпирическую функцию распределения:

Рис. 1 РИСУНОК НЕ СООТВЕТСТВУЕТ

График функции приведен на рис.1:

Пример 15.2. По десяти наблюдениям над случайной величиной получена выборка: 11; 12; 10; 10; 12; 10; 13; 11; 10; 11. Построить ряд распределения относительных частот и эмпирическую функцию распределения.

Решение.

1) Постоим вариационный ряд: 10; 10; 10; 10; 11; 11; 11; 12; 12; 13.

2) Построим ряд распределения частот и относительных частот в одной таблице, где относительную частоту определяем по формуле .

	10	11	12	13
	4	3	2	1
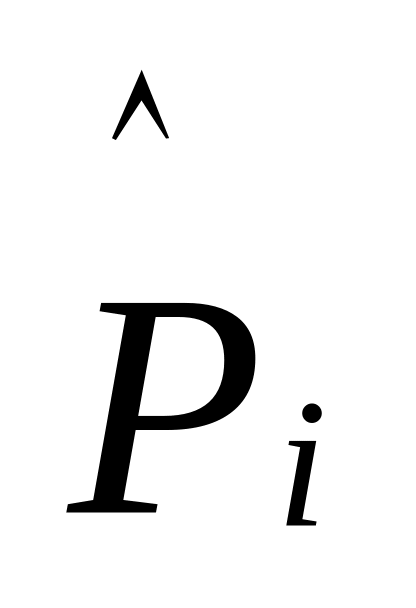
	0.4	0.2	0.3	0.1

Например . Аналогично находим все остальные значения.

3) По ряду распределения относительных частот строим эмпирическую функцию распределения . Имеем:

Рис. 2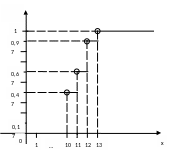

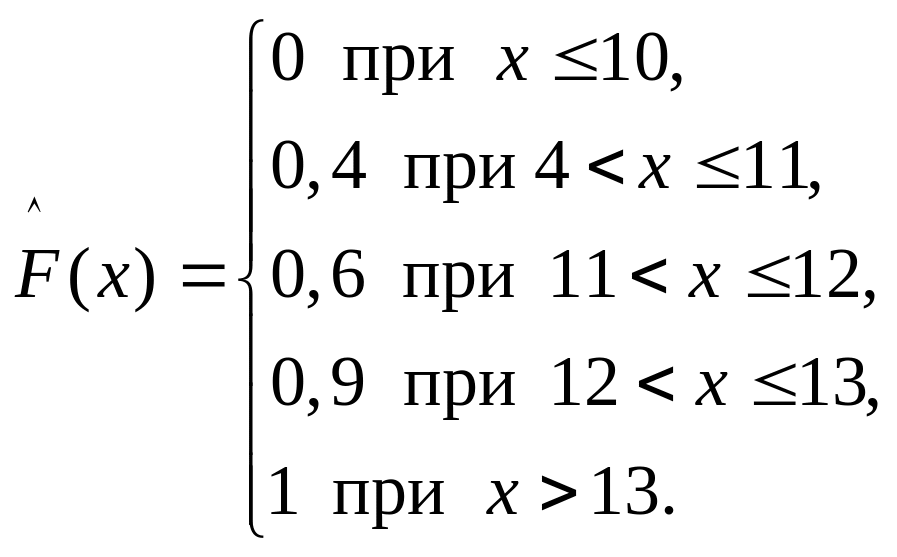
График этой функции приведен на рис.2:

Задачи для самостоятельного решения

1) По десяти наблюдениям над случайной величиной получена выборка: 3; 5; 7; 8; 5; 8; 8; 5; 10; 7. Построить вариационный ряд, ряд распределения частот и эмпирическую функцию распределения.

2) По десяти наблюдениям над случайной величиной получена выборка: 4; 6; 7; 8; 8; 7; 4; 4; 6; 7. Построить вариационный ряд, ряд распределения относительных частот и эмпирическую функцию распределения.

4.3. Полигон, гистограмма, кумулята

Пример 16.1. По приведенным ниже данным о квалификации рабочих цеха требуется: 1) построить вариационный ряд; 2) дать графическое изображение ряда в виде полигона частот и относительных частот; 3) вычислить средний тарифный разряд рабочего, моду и медиану.

Тарифные разряды 25 рабочих цеха:

4; 3; 6; 4; 4; 2; 3; 5; 4; 4; 5; 2; 3; 4; 4; 5; 2; 3; 6; 5; 4; 2; 4; 3; 5.

Решение.

1) Строим вариационный ряд: 2; 2; 2; 2; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 4; 4; 4; 5; 5; 5; 5; 5; 6; 6.

2) Строим дискретный ряд распределения частот и относительных частот:

	2	3	4	5	6
	4	5	9	5	2

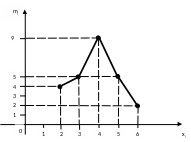
Рис. 3

Строим полигон частот и полигон относительных частот (рис. 3). Полигон частот - ломаная, звенья которой соединяют точки с координатами ( , ).

Рис. 4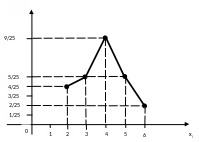

По этим же данным строим полигон относительных частот? Учитывая, что , .

3) Находим средний тарифный разряд рабочего, моду и медиану.

Строим вспомогательную таблицу:

Тарифный разряд,	Число рабочих,	Накопленная частота, S
2 3 4 5 6	4 5 9 5 2	4 9 18 23 25

Итого: 25

Средний тарифный разряд определяется по формуле среднего арифметического:

,

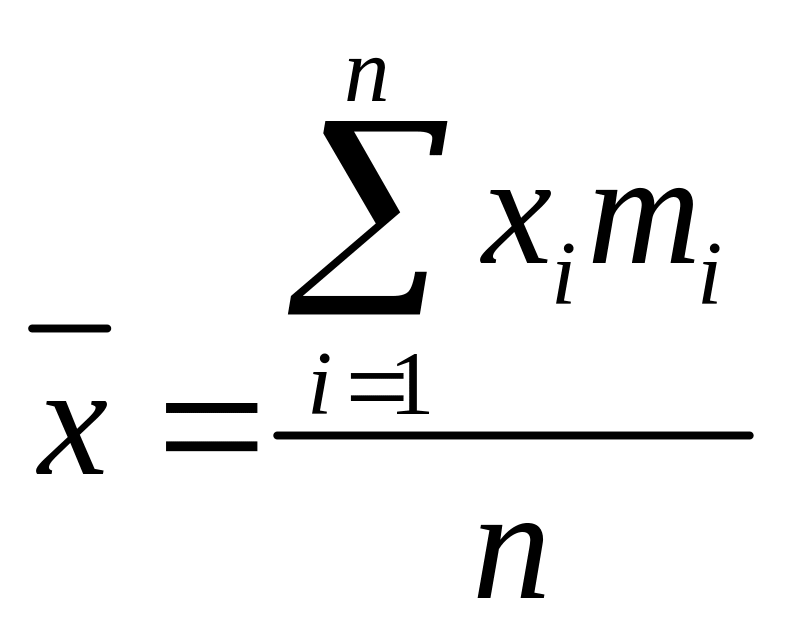где x_i - индивидуальное значение признака (варианта). Имеем:

.

Мода:

= 4-му разряду (4-й разряд встречается 9 раз, это наибольшая частота).

Медиана:

.

= 4-му разряду (т.к. номер 13 соответствует 4 разряду).

Пример 16.2. Ниже приведены данные о распределении рабочих участка по стажу работы:

Стаж работы (лет), xi	До 5	5-10	10-15	15-20	20 и более
Число рабочих, mi	2	3	14	6	5

Дать графическое изображение ряда, вычислить средний стаж работы рабочего, моду и медиану.

Решение.

1) Графическое изображение ряда может быть представлено в виде гистограммы, полигона и кумуляты.

Для построения графиков строим таблицу :

Таблица

Стаж работы (лет),				,	Накопленная частота,
До 5 5-10 10-15 15-20 20 и более	2 3 14 6 5	2/30 3/30 14/30 6/30 5/30	2/5 3/5 14/5 6/5 1	2/150 3/150 14/150 6/150 5/150	2 5 19 25 30

Итого: 30

Здесь - число рабочих , объем выборки n = 30, длина интервала h =5, – относительная частота рабочих по стажу работы (например, ), – плотность частоты (например, ), – плотность относительной частоты (например, ).

2) Построение гистограммы, полигона и кумуляты.

2А Гистограмма частот представляет собой ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы, а высоты представляют собой отношение числу рабочих , а площадь всей фигуры равна объему выборки (рис.5). Для построения полигона частот соединим середины верхних оснований прямоугольников ломаной линией.

Рис. 5

Рис. 6

Аналогичным образом строится гистограмма и полигон относительных частот, только высоты будут представлять собой отношение , а площадь всей фигуры будет равна единице (рис.6).

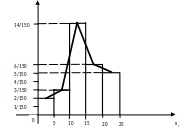
Рис. 7 ПОПРАВИТЬ: Х=5, S=2 Х=15, S=19

2Б. Кумулята строится по накопленным частотам (частостям). По вертикальной оси откладываются накопленные частоты (частости, в нашем примере приведены в последнем столбце таблицы ), а по горизонтальной длина интервалов. При построении кумуляты нижней границе первого интервала соответствует частота равная нулю, а верхней границе вся частота данного интервала (рис.7).

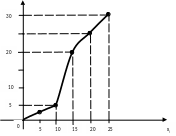
S

3) Средний стаж работы рабочего участка определяется по формуле:

,

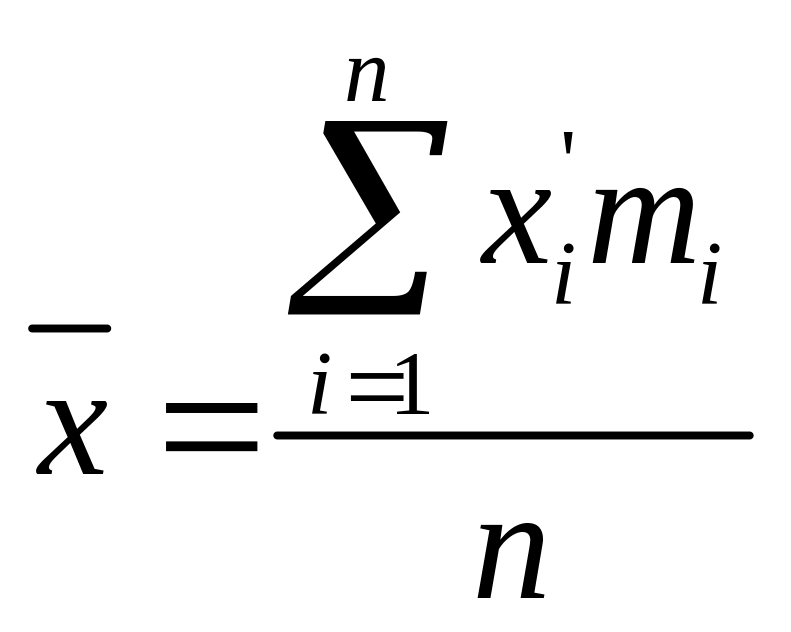- середина интервала;

(лет)

Мода Мо соответствует интервалу 10-15.

;

, , , , .

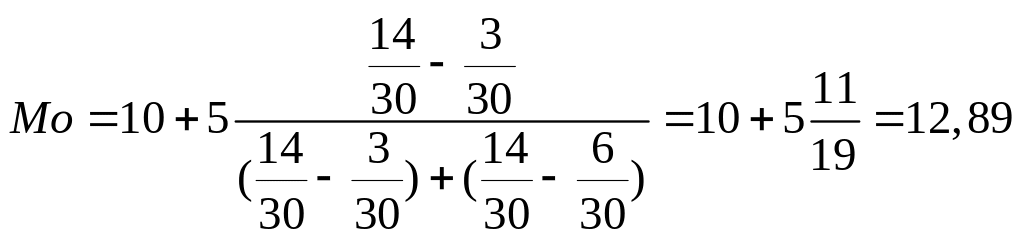(лет).

Место медианы определяется по её номеру: (лет).

По номеру определяем медианный интервал 10-15.

,

, , , , .

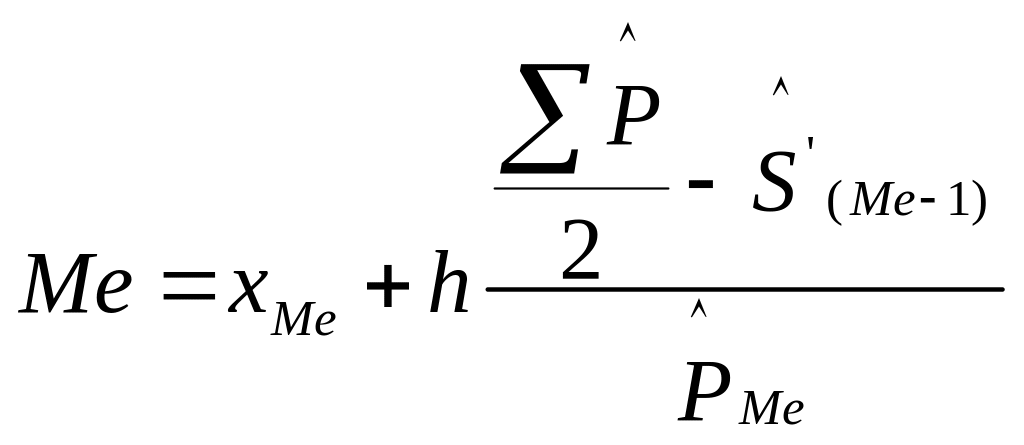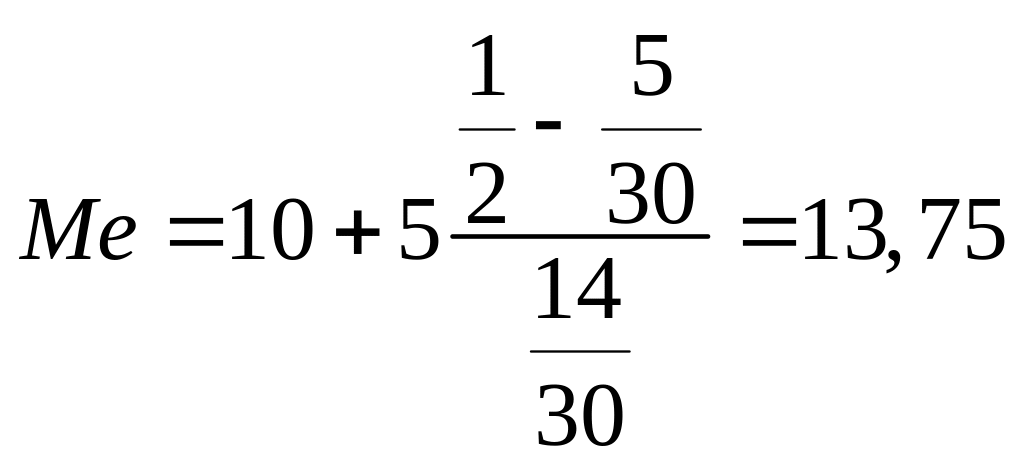(лет).