Задачи для самостоятельного решения

1. Время работы светодиода есть случайная величина с показательным законом распределения. Среднее время безотказной работы светодиода Какова вероятность того, что время безотказной работы светодиода будет не менее 600 часов?

2. Длительность работы элемента некоторого устройства есть случайная величина , функция плотности распределения которой

.

Требуется найти среднее время работы элемента и вероятность того, что элемент проработает не более 400 часов.

3. Средняя продолжительность разговора продавца с покупателем составляет 2 минуты. Какова вероятность того, что разговор с произвольным покупателем будет продолжаться не более 3 минут, если время разговора есть случайная величина , имеющая показательный закон распределения?

4. Случайная величина имеет показательный закон распределения с параметром λ = 3. Какова вероятность попадания случайной величины в интервал ?

5. В центре занятости среднее время обслуживания клиента – 10 минут. Какова вероятность того, что за один час будет обслужено два клиента, если время обслуживания есть случайная величина с показательным законом распределения?

6. Мастер по ремонту обуви в среднем тратит на одного клиента 25 минут. Какова вероятность того, что за один час мастер обслужит менее двух клиентов, если время обслуживания есть случайная величина с показательным законом распределения?

7. Непрерывная случайная величина имеет показательный закон распределения с параметром λ = 2. Составить функцию плотности и функцию распределения. Найти числовые характеристики и вероятность того, что случайная величина попадёт в интервал ?

8. Длительность безотказной работы двух микросхем имеет показательный закон распределения, функции распределения которых соответственно равны: и . Какова вероятность того, что за 10 часов работы откажут обе микросхемы?

9. Время ремонта автомобиля есть случайная величина , имеющая показательный закон распределения. Какова вероятность того, что время ремонта некоторого автомобиля будет менее 16 дней, если среднее время ремонта автомобиля равно 8 дней?

10. Длительность безотказной работы двух независимо работающих светодиодов имеет показательный закон распределения, функции распределения которых соответственно равны:

и .

Какова вероятность того, что за 10 часов работы откажет только один светодиод?

Раздел четвёртый. Математическая статистика

4.1. Вариационный ряд

Пример 14.1. Представлены данные о стаже работы в годах 15 работников рекламного агентства: 6; 4; 5; 3; 3; 5; 5; 6; 3; 7; 4; 5; 2; 4; 5.

Требуется: 1) построить вариационный ряд; 2) найти моду и медиану.

Решение. 1) Расположим данные о стаже работы сотрудников в возрастающем порядке: 2; 3; 3; 3; 4; 4; 4; 5; 5; 5; 5; 5; 6; 6; 7. Получили вариационный (ранжированный) ряд.

2) Мода и медиана – показатели центра распределения. Мода – наиболее часто встречающееся значение признака. = 5(лет), т.к. стаж работы 5 лет встречается здесь чаще всего.

3) Медиана определяется по её номеру:

, где – общее число членов ряда. Отсюда:

= 8, = 5(лет), так как номеру 8 соответствует значение стажа работы 5 лет.

Пример 14.2. Дана дневная производительность труда рабочих бригады выполняющих одинаковую операцию по обработке детали в (шт): 18;20;20;20;21;21;19;19;19;22;22;23;22;20;20;23;20;21;21;21.

Требуется: 1) составить вариационный ряд; 2) найти моду и медиану.

Решение. Расположим представленные данные в возрастающем порядке: 18; 19; 19; 19; 20; 20; 20; 20; 20; 20; 21; 21; 21; 21; 21; 22; 22; 22; 23; 23.

Получили вариационный ряд, в котором = 20 членов. = 20 (шт), т.к. дневная производительность труда рабочих 20 шт. встречается с наибольшей частотой равной 6.

Если ряд содержит четное число значений признака, то медиана определяется по формуле:

, . Следовательно , шт; шт.

Отсюда = 20,5 (шт).

Пример 14.3. Имеются данные о возрастном составе группы студентов вечернего отделения (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 20.

Требуется: 1) построить интервальный ряд распределения; 2) определить средний возраст студентов вечернего отделения; 3) численное значение моды и медианы.

Решение. 1) Построим интервальный вариационный ряд: 18; 20; 22; 22; 23; 24; 24; 25; 25; 26; 26; 27; 27; 28; 28; 28; 29; 29; 29; 29; 30; 31; 31; 32; 32; 33; 34; 35; 38; 38.

Для построения интервального вариационного ряда величина интервала определяется по формуле: , где R - размах колебания (варьирование признака).

– разность между максимальным и минимальным значениями признака, – число групп. приближенно определяется по формуле Стерджесса: , где – общее число единиц совокупности.

, .

;

(округляется всегда в большую сторону); (года) – округляем числа до целого большего.

Нижнюю границу первого интервала принимают равной минимальному значению признака, верхняя граница первого интервала соответствует значению . Если единица обладает значением, соответствующим верхней границе интервала, то её относят к следующему интервалу.

Группы студентов по возрасту (лет), ( )	Число студентов,	Накопленная частота, S
18-22 22-26 26-30 30-34 34-38	2 7 11 6 4	2 9 20 26 30

Итого: 30

Находим модальный интервал 26-30. Ему соответствует наибольшее число студентов - 11.

Мода определяется по формуле:

;

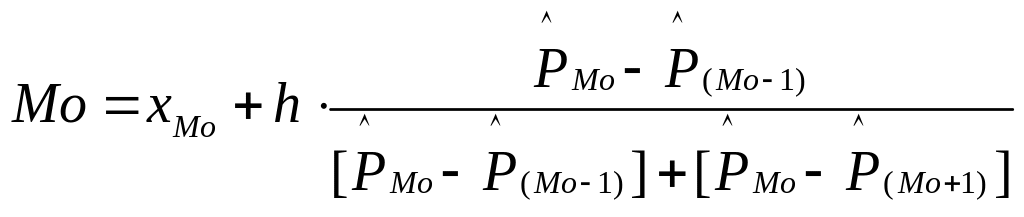(лет) – нижняя граница модального интервала;

h = 4 (лет) – длина частичного интервала;

– относительная частота (частость) модального интервала;

– частость интервала, предшествующего модальному;

– частость интервала, следующего за модальным;

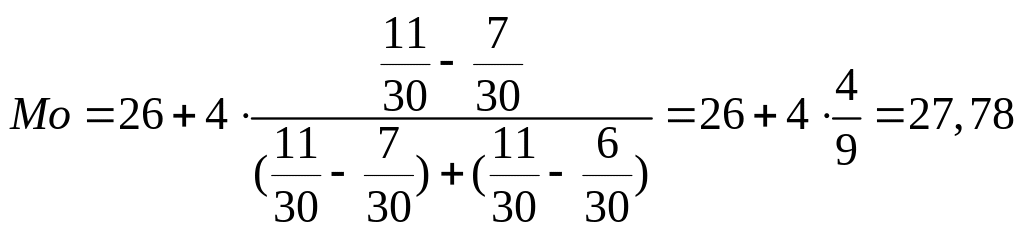(лет)

Медиана соответствует значению признака, стоящему в середине вариационного (ранжированного) ряда.

Положение медианы определяется по её номеру .

Медианный интервал определяется по накопленным частотам 26-30. Медиана определяется по формуле:

.

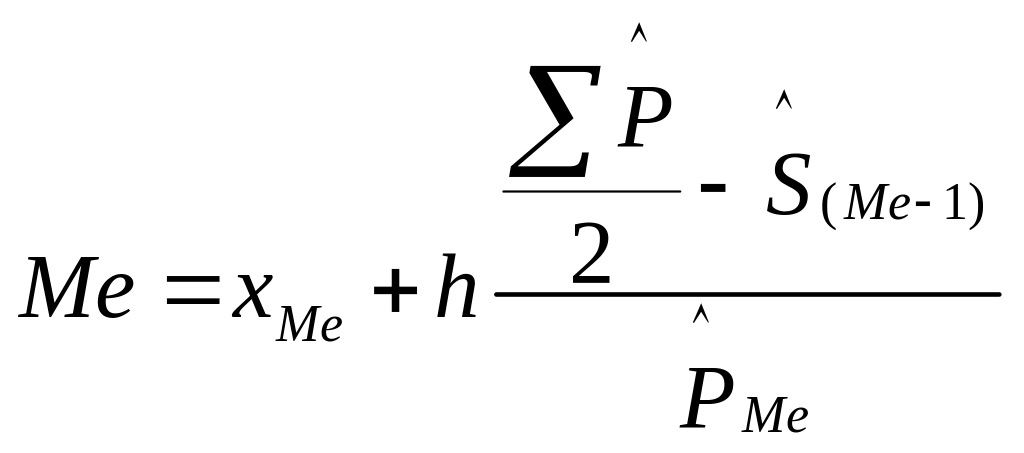- половина суммы накопленных частостей;

- частость медианного интервала;

- накопленная частость интервала, предшествующего медианному.

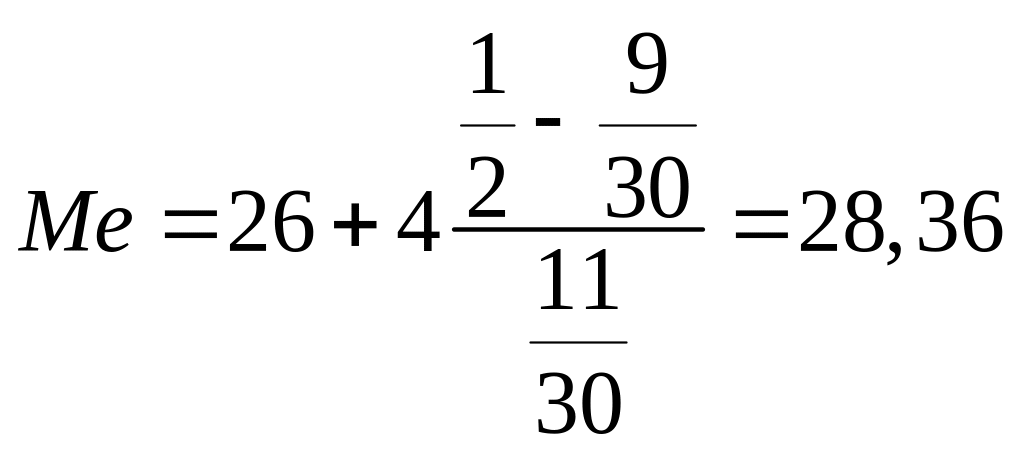, (лет).