Типовые задачи базового уровня учебной дисциплины «математика» с решениями (третий семестр, часть 2)

для студентов бакалавриата по направлениям:

«Менеджмент» 080 200

«Прикладная информатика» 230 700

«Управление персоналом» 080 400

«Экология и природопользование» 022 000

«Социология» 040 100

МОСКВА 2013

Содержание

Предисловие ..…………………………………………………….…. 4

3.3. Нормальный закон распределения ……………………….…. 5

3.4. Показательный закон распределения ……………………….….8

РАЗДЕЛ ЧЕТВЕРТЫЙ. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА ……..13

4.1. Вариационный ряд ……………………….…………………… 13

4.2. Эмпирическая функция распределения ……………………… 17

4.3. Полигон, гистограмма, кумулята ……………………………… 19

4.4. Показатели асимметрии и эксцесса ……………………….…… 27

4.5. Статистические оценки параметров распределения ………….28

3.3. Нормальный закон распределения

Пример 12.1. Случайная величина задана плотностью распределения вероятностей:

.

Построить график функции плотности распределения. Найти её математическое ожидание и дисперсию .

Решение.

Рис. 1 РИСУНОК

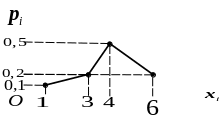
Так как случайная величина имеет нормальный закон распределения, то из условия следует, что , а .

Пример 12.2. Случайная величина имеет нормальный закон распределения с математическим ожиданием и среднеквадратическим отклонением . Какова вероятность того, что в результате испытания значение случайной величины окажется в интервале ?

Решение. Так как интервал несимметричен относительно математического ожидания , то для решения задачи используем

формулу: , откуда

,

где – функция Лапласа, значения которой находим по соответствующей таблице.

Пример 12.3. Размер детали есть случайная величина с нормальным законом распределения, математическое ожидание которой , а среднеквадратическое отклонение . Какова вероятность того, что при изготовлении детали её размер окажется в интервале ?

Решение. Так как интервал симметричен относительно математического ожидания а = 13, то для решения задачи используем формулу: , откуда

.

Пример 12.4. После изготовления детали контролируется её размер. Ошибка измерения контролируемого размера детали есть случайная величина , имеющая нормальный закон распределения с математическим ожиданием и среднеквадратическим отклонением мм. Какова вероятность того, что ошибка измерения будет менее 17 мм?

Решение. Так как ошибка измерения есть случайная величина с нормальным законом распределения и возможными значениями, симметричными относительно математического ожидания , то для решения задачи используем формулу: , откуда

.

Пример 13.5. Размер изготавливаемой на станке детали представляет собой случайную величину, подчинённую нормальному закону распределения. Средний размер детали мм, а среднеквадратическое отклонение мм. Найти вероятность того, что отклонение размера детали при её изготовлении не превысит допуска мм?

Решение. Так как отклонение размера детали симметрично относительно математического ожидания, то для решения задачи используем формулу: ,

откуда следует, что у 31% деталей отклонение размера будет в пределах заданного допуска.