
- •Содержание
- •Требования к оформлению контрольных работ
- •Формирование исходных данных к задачам
- •2.1.2*. Прямая на плоскости.
- •2.2 Прямая и плоскость в пространстве.
- •8.2. Случайные величины.
- •Раздел 9. Математическая статистика.
- •9.1. Численная обработка данных одномерной выборки.
- •9.2. Построение уравнений прямой регрессии.
- •Раздел 10. Линейное программирование.
- •10.1. Задача оптимального производства продукции.
- •10.2 Транспортная задача.
- •10.3. Матричные игры.
- •Раздел 11. Математические методы в экономике.
- •11.1. Сетевое планирование.
- •11.2. Системы массового обслуживания (смо).
- •11.3. Задача межотраслевого баланса.
- •Список учебной литературы
2.1.2*. Прямая на плоскости.
На прямую
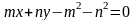 ,
способную отражать лучи, падает луч,
лежащий на прямой, заданной уравнением
,
способную отражать лучи, падает луч,
лежащий на прямой, заданной уравнением
 .
Составить уравнение прямой, на которой
лежит отраженный луч.
.
Составить уравнение прямой, на которой
лежит отраженный луч.
2.2 Прямая и плоскость в пространстве.
2.2.1
Пирамида SАВС
задана вершинами
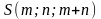 ,
,
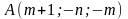 ;
;
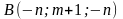 ,
,
 .
Найти:
.
Найти:
а) уравнение плоскости, проходящей через точки А, В и С;
б) величину угла между ребром SC и гранью АВС;
в) величину угла между ребром SC и ребром СВ;
г) величину угла между гранью АВС и гранью АCS ;
д) площадь грани АВС;
е) уравнение высоты SН, опущенной из вершины S на грань АВС;
ж) длину высоты SН;
з) объем пирамиды SABC(двумя способами).
2.3 Векторная алгебра.
2.3.1 В
базисе векторов
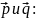 (
( )
)
заданы
вектора
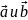 :
:
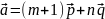
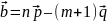
Найти:
а) косинус угла между векторами ;
б) площадь параллелограмма, построенного на векторах
2.3.2
Пирамида АВСD
задана вершинами
;
,
,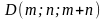 .
Найти:
.
Найти:
а) угол между векторами АВ и AС;
б) объем пирамиды ABCD
в) длину высоты DН, опущенной из вершины D на грань АВС.
Раздел 3. Дифференциальное исчисление.
3.1. Построение графиков элементарных функций.
3.1.1. С
помощью смещения, растяжения и отражения
графиков функций
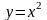 и
и
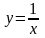 построить графики функций:
построить графики функций:
а)
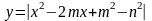 ;
б)
;
б)
 .
.
3.2. Пределы, непрерывность и разрывы функций.
3.2.1. Найти пределы функций:
а)
 ;
б)
;
б)
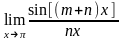 ;
;
в)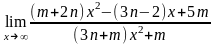 ;
г)
;
г)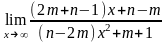 ;
;
д)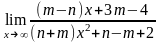 ;
е)
;
е) ;
;
ж)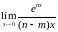 ;
з*)
;
з*) ;
;
и) ;
к)
;
к)
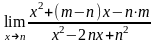 ;
;
л)
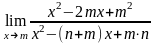 ;
м*)
;
м*)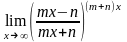 .
.
3.2.2. В
точках
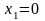 и
и
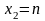 для функции
для функции
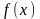 установить непрерывность или определить
характер точек разрыва. Нарисовать
график функции
в окрестностях этих точек:
установить непрерывность или определить
характер точек разрыва. Нарисовать
график функции
в окрестностях этих точек:
а) ;
б*)
;
б*)
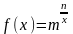 .
.
3.3. Производные функций.
3.3.1.
Найти производные
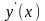 функций:
функций:
а) y = mx + n;
б) y = mxn;
в)
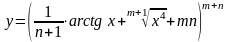 ;
;
г)
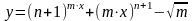 ;
;
д)
 ;
;
е)
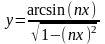 ;
;
ж)
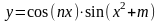 ;
;
з)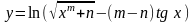 ;
;
и*)
 ;
;
к*)
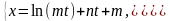
3.4. Приложения производной.
3.4.1.
Составить уравнения касательных к
графику функции
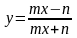 :
:
а) в
точке А( ;
0 );
;
0 );
б*)
параллельных прямой
 .
.
3.4.2.
Найти наибольшее и наименьшее значения
функции
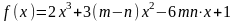 на отрезке
на отрезке
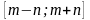 .
.
3.4.3*. С
помощью методов дифференциального
исчисления исследовать функцию
 и построить ее график.
и построить ее график.
Раздел 4. Функции нескольких переменных.
4.1. Частные производные и дифференциал функции.
4.1.1.
Найти частные производные
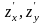 и
и
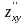 функций:
функций:
а)
 ;
;
б)
 .
.
4.1.2.
Найти полный дифференциал функции
 .
.
4.1.3.
Показать, что функция
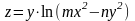 удовлетворяет уравнению
удовлетворяет уравнению
 .
.
4.2. Приложения частных производных.
4.2.1.
Составить уравнения касательной
плоскости и нормали к поверхности
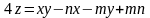 в точке
в точке
 .
.
4.2.2. Для
функции
 в точке
в точке
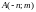 найти градиент и производную по
направлению
найти градиент и производную по
направлению
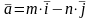 .
.
4.2.3.
Найти экстремумы функции
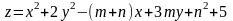
4.2.4*.
Найти наибольшее и наименьшее значения
функции
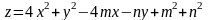 в области, заданной неравенствами:
в области, заданной неравенствами:
 ;
;
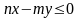 ;
;
 .
.
Раздел 5. Интегральное исчисление.
5.1. Неопределенный интеграл.
5.1.1. Найти интегралы:
а)
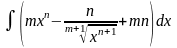 ;
;
б)
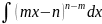
в)
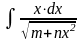 ;
;
г)
 ;
;
д)
 ;
;
е)*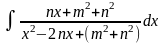
ж)* .
.
5.2. Несобственные интегралы.
5.2.1. Вычислить интегралы или установить их расходимость:
а)
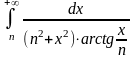 ;
;
б)
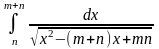 .
.
5.3. Применение интегралов.
5.3.1. Найти площадь фигуры, ограниченной линиями:
а)
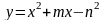 ,
,  ,
,
построить схематически чертеж в декартовых координатах;
б)
 ,
,
построить схематически чертеж в полярных координатах.
5.3.2*. Найти объем тела, полученного при вращении вокруг оси OX фигуры, ограниченной линиями, сделав чертеж:
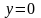 ,
, 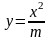 ,
, 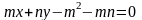 .
.
5.4. Приближенное вычисление определенных интегралов.
5.4.1. Для
вычисления определенного интеграла
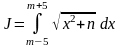 ,
разбивая отрезок интегрирования сначала
на 10 равных частей, а затем на 20 равных
частей, найти приближенное значение
,
разбивая отрезок интегрирования сначала
на 10 равных частей, а затем на 20 равных
частей, найти приближенное значение
 и
и
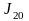 :
:
а) по формуле трапеций;
б*) по формуле Симпсона.
Оценить точность приближения.
Раздел 6. Дифференциальные уравнения.
6.1. Уравнения первого порядка.
6.1.1. Найти общее решение уравнения:
а)y = mx-n
б) y = mxn-n
в)
 ;
;
г)
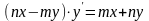 ;
;
д)
 ;
;
е*)
 .
.
6.1.2*. Скорость роста банковского вклада пропорциональна с коэффициентом равным величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составляла миллионов рублей.
6.2. Линейные уравнения высших порядков.
6.2.1. Решить задачу Коши для дифференциального уравнения второго порядка:
а)
 ,
,
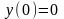 ,
,  ;
;
б)
 ,
, 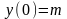 ,
,
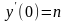 ;
;
в)*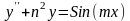 ,
,
,
,  .
.
Раздел 7. Ряды.
7.1. Числовые ряды.
7.1.1. Исследовать на сходимость ряды с положительными членами:
а)
 ;
;
б)
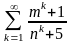 ;
;
в)*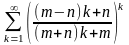 ;
;
г)* .
.
7.1.2. Установить характер сходимости знакочередующихся рядов:
а)
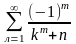 ; б)*
; б)*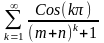 .
.
7.2. Степенные ряды.
7.2.1. Найти интервал сходимости степенного ряда, исследовать поведение ряда на концах интервала сходимости:
а)
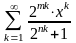 ;
;
б)
 ;
;
в*)
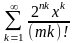 .
.
7.2.2.
разложить функцию
в ряд Тейлора в окрестности точки
 :
:
а)
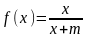 ,
,  ;
;
б)
 ,
, 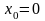 .
.
7.2.3. С помощью разложения в ряд вычислить приближенно с точностью 0,001 значения:
а)
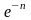 ;
;
б)
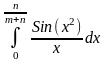 .
.
Раздел 8. Теория вероятностей.
8.1. Вероятности событий.
8.1.1. Из
группы в
 человек необходимо выбрать двух: одного
для работы летом в приемной комиссии,
другого – в помощь деканату для подготовки
к новому учебному году. Сколькими
способами это можно сделать?
человек необходимо выбрать двух: одного
для работы летом в приемной комиссии,
другого – в помощь деканату для подготовки
к новому учебному году. Сколькими
способами это можно сделать?
8.1.2. Директор фирмы заключил договоров. Пять из них, вопреки советам юриста он заключил с нарушением налогового законодательства. Найти вероятность того, что при налоговой проверке среди наудачу взятых пяти договоров, три окажутся без нарушений законодательства?
8.1.3.
Ведутся поиски
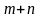 преступников. Каждый из них независимо
от других может быть обнаружен в течение
суток с вероятностью
преступников. Каждый из них независимо
от других может быть обнаружен в течение
суток с вероятностью
 .
Какова вероятность того, что в течении
суток будет обнаружен: а) хотя бы один
преступник;
б) ровно два преступника;
в) не менее двух преступников.
.
Какова вероятность того, что в течении
суток будет обнаружен: а) хотя бы один
преступник;
б) ровно два преступника;
в) не менее двух преступников.
8.1.4. Курсант производит независимых выстрелов по мишени с вероятностью попадания 0,2. Найти вероятность: а) двух попаданий; б) не менее двух попаданий; в) не более одного.
8.1.5. Оперативный дежурный МВД по г. Москве в среднем регистрирует преступлений за 2 часа. Поток регистрируемых преступлений практически подчиняется закону Пуассона. Определить вероятность того, что: а) за час(ов) будет зарегистрировано 2 преступления; б) за час(ов) будет зарегистрировано хотя бы 1 преступление; в) за час(ов) будет зарегистрировано не более 2-х преступлений.
8.1.6.
Вероятность того, что клиент банка не
вернет заем в период экономического
роста, равна
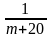 ,
а в период экономического кризиса —
.
Предположим, что вероятность того, что
начнется период экономического роста,
равна 0,65. Чему равна вероятность того,
что случайно выбранный клиент банка не
вернет полученный кредит?
,
а в период экономического кризиса —
.
Предположим, что вероятность того, что
начнется период экономического роста,
равна 0,65. Чему равна вероятность того,
что случайно выбранный клиент банка не
вернет полученный кредит?
