Задача 22.
В задачах
211 – 240 дана функция
.
Исследовать
функцию и построить ее график по схеме:
найти область определения функции;
вияснить, есть ли данная функция четной, ненечетной или общего вигда;
исследовать функцию на непрерывность; найти точки розрыва и односторонние пределы в точках розрыва;
определить интервалы возростания и убывания функции и точки ее экстремума;
определить интервалы выпуклости и вогнутости и точки перегиба графика функции;
найти асимптоты графика функции;
по данным пунктов 1-6 построить график функции.
211.
|
212.
|
213.
|
214.
|
215.
|
216.
|
217.
|
218.
|
219.
|
220.
|
221.
|
222.
|
223.
|
224.
|
225.
|
226.
|
227.
|
228.
|
229.
|
230.
|
231.
|
232.
|
233.
|
234.
|
235.
|
236.
|
237.
|
238.
|
239.
|
240.
|
Задача 23.
В задачах 301 – 330 вычислить интегралы.
301.
а)
б)
|
в) г) |
302. а)
б)
|
в)
г)
|
303. а)
б)
|
в)
г)
|
304. а)
б)
|
в)
г)
|
305. а)
б) |
в)
г)
|
306. а)
б)
|
в)
г)
|
307. а)
б)
|
в)
г)
|
308. а)
б)
|
в)
г)
|
309. а)
б)
|
в)
г)
|
310. а)
б)
|
в)
г)
|
311. а)
б)
|
в)
г)
|
312. а)
б)
|
в)
г)
|
313.а) б) |
в)
г)
|
314. а)
б)
|
в)
г)
|
315.а)
б)
|
в)
г)
|
316. а)
б)
|
в)
г)
|
317.а) б) |
в)
г)
|
318.а) б) |
в)
г)
|
319. а)
б)
|
в)
г)
|
320. а)
б)
|
в)
г)
|
321. а)
б)
|
в)
г)
|
322. а)
б)
|
в)
г)
|
323. а)
б)
|
в)
г)
|
324. а)
б)
|
в)
г)
|
325. а)
б)
|
в) г)
|
326. а)
б)
|
в) г)
|
327. а)
б)
|
в)
г)
|
328. а)
б)
|
в)
г)
|
329.
а)
б)
|
в)
г)
|
330. а)
б)
|
в) г)
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
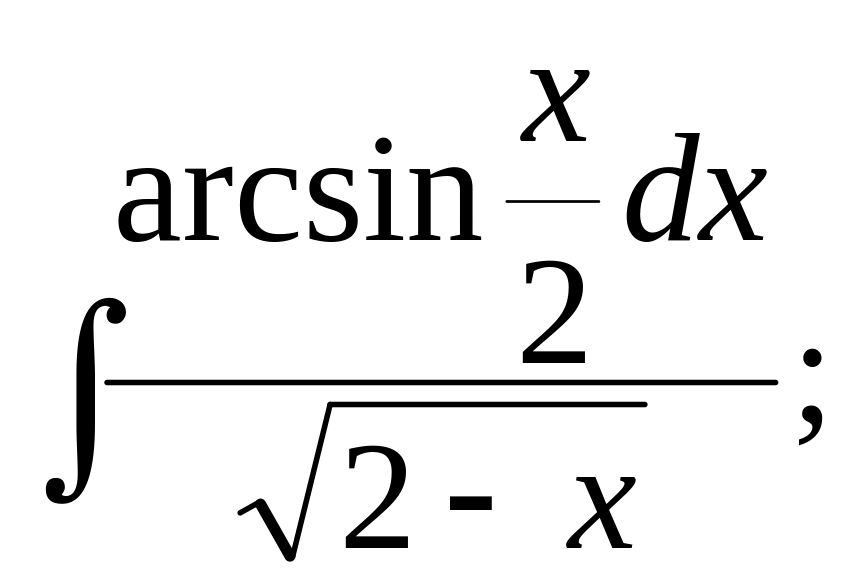
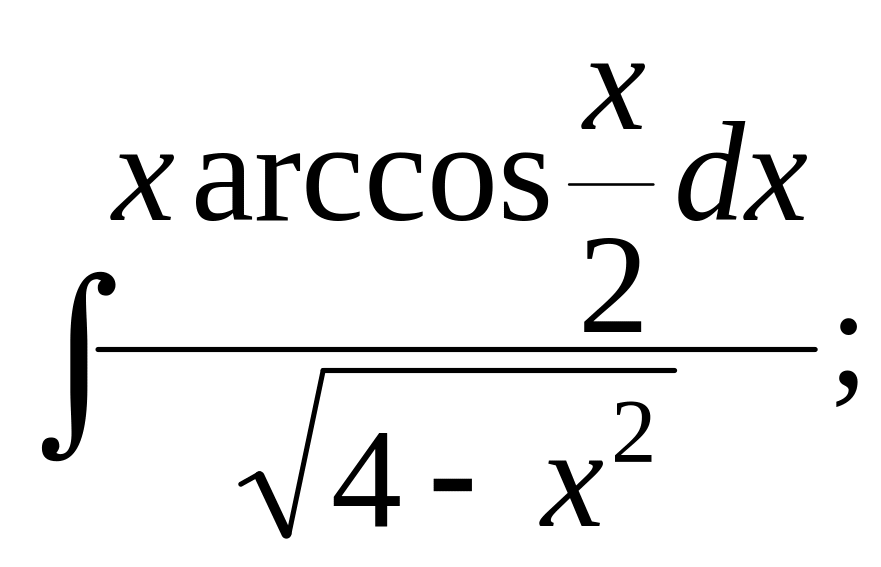
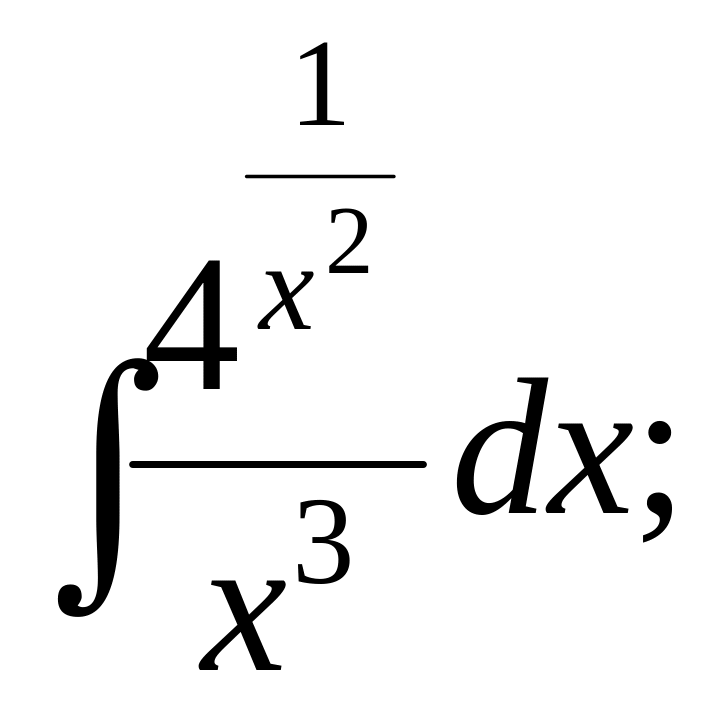
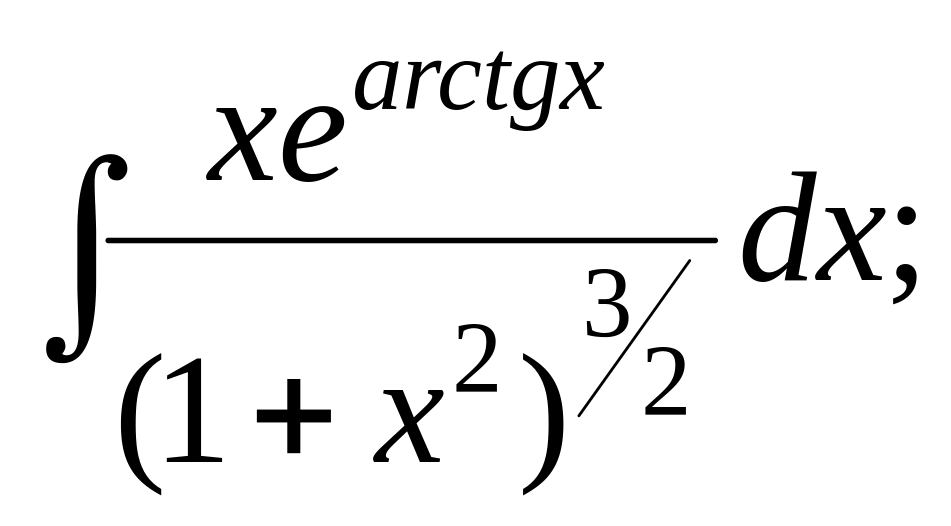
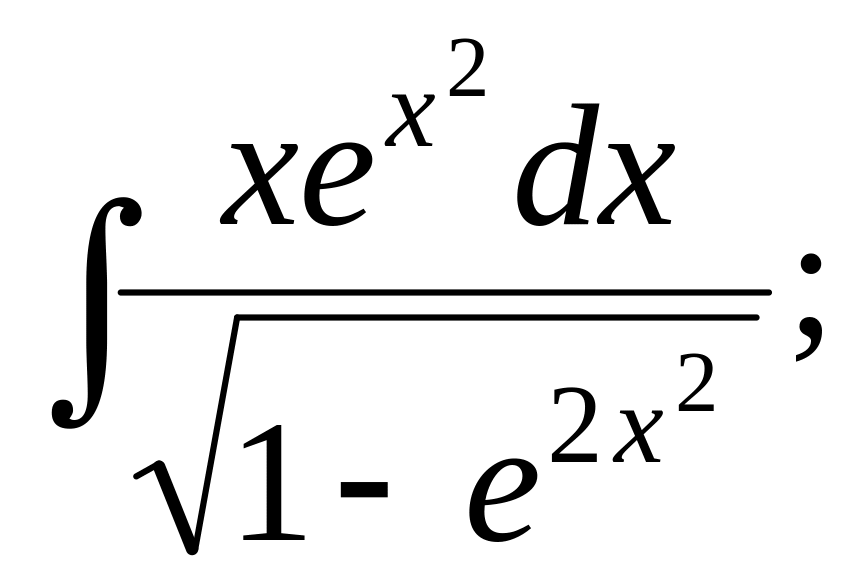
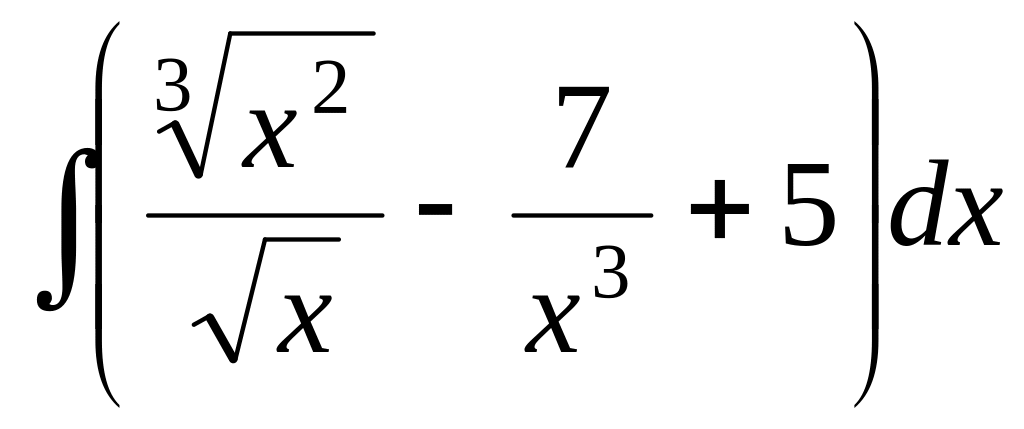