Практическое занятие 6. Статистическая проверка гипотез

Выбор и использование гипотезы совпадения экспериментального среднего и известного значения; гипотезы совпадения двух независимых средних величин; гипотезы о линейности данных.

1. Гипотеза совпадения экспериментального среднего и известного значения.

Задача 1.1. Рассмотрим набор результатов x₁, x₂, …, x_n многократного измерения нормально распределенной величины x. Проверяется гипотеза о том, что 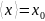, где – заданное значение измеряемой величины, равное 10.

n	x
1	10.52
2	10.62
3	10.82
4	10.91
5	10.54
6	10.57
7	10.92
8	10.65
9	10.58
10	10.26

Решение №1:

1. Определим и :

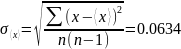
2. Введем новую величину, содержащую как экспериментальное среднее, так и заданное значение:

=10.083

3. При уровне значимост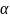и   гипотеза о совпадении и подтверждена, если 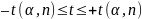, чему соответствует доверительная вероятность α. При α=0.95:

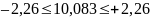
4. Заданное значение t не попадает в найденный интервал, гипотезу о совпадении и x₀ нужно расценивать как несправедливую для уровня значимости α=0,95.

Решение №2:

1. Определим :

2. Найдем интервал возможного изменения величины . Воспользуемся

3. Заданное значение x₀ не попадает в найденный интервал, гипотезу о совпадении и x₀ нужно расценивать как несправедливую для уровня значимости α=0,95.

2. Гипотеза совпадении двух независимых средних значений

Задача 2.1. Рассмотрим следующую ситуацию. Из двух независимых экспериментов получены две группы результатов многократных измерений x₁, x₂,.......,x_n1 и y₁, y₂,....y_n2 нормально распределенных величин x и y.

n	x	y
1	10.52	10.54
2	10.62	10.51
3	10.82	10.84
4	10.91	10.45
5	10.54	10.56
6	10.57	10.23
7	10.92	10.42
8	10.65	10.74
9	10.58	10.69
10	10.26	10.85

Проверяют гипотезу о том, что  .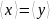

Решение:

4. Определены .

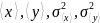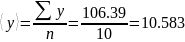
5. Введем новую величину:

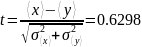
6. При справедливости равенства для 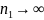и 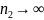установлено, что при конечных значениях n₁ и n₂ распределение величины t близко к распределению Стьюдента, у которого:

7. При уровне значимости   гипотеза о совпадении и подтверждена, если –t(α, n)<= t<= +t( ,n), чему соответствует доверительная вероятность α.

8. При α=0.7