- •Практическое занятие 5. Использование метода наименьших квадратов
- •Практическое занятие 5. Использование метода наименьших квадратов Вариант №1
- •Практическое занятие 5. Использование метода наименьших квадратов Вариант №2
- •Практическое занятие 5. Использование метода наименьших квадратов Вариант №3
- •Практическое занятие 5. Использование метода наименьших квадратов Вариант №4
- •Практическое занятие 5. Использование метода наименьших квадратов Вариант №5
Практическое занятие 5. Использование метода наименьших квадратов
Линеаризация данных.
Использование метода наименьших квадратов.
Задача 1.
Исследовалось основное уравнение динамики вращательного движения ε = M/J (прямая, проходящая через начало координат). При различных значениях момента M измерялось угловое ускорение ε некоторого тела.
Требуется определить момент инерции этого тела. Результаты измерений момента силы и углового ускорения занесены во второй и третий столбцы таблицы 1.
Таблица 1
n |
M, Н · м |
ε, c-1 |
M2 |
M · ε |
ε – kM, 10-3 |
(ε - kM )2 |
1 |
1.44 |
0.52 |
2.0736 |
0.7488 |
0.039432 |
0.001555 |
2 |
3.12 |
1.06 |
9.7344 |
3.3072 |
0.018768 |
0.000352 |
3 |
4.59 |
1.45 |
21.0681 |
6.6555 |
-0.08181 |
0.006693 |
4 |
5.90 |
1.92 |
34.81 |
11.328 |
-0.049 |
0.002401 |
5 |
7.45 |
2.56 |
55.5025 |
19.072 |
0.073725 |
0.005435 |
∑ |
– |
– |
123.1886 |
41.1115 |
– |
0.016436 |
Решение:
Формула
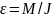 может
быть представлена в виде формулы прямой,
проходящей через начало координат:
может
быть представлена в виде формулы прямой,
проходящей через начало координат:
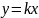 ,
где
,
где
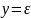 ;
;
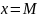 ;
;
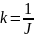 .
.Метод наименьших квадратов утверждает, что для k следует выбирать такое значение, при котором φ имеет минимум:
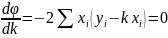 (1)
(1)
или
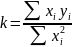 (2)
(2)
По формуле (2) определяем:
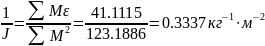
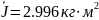
Для определения среднеквадратичной ошибки воспользуемся формулой (3):
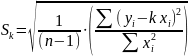 (3)
(3)
где – n число измерений.
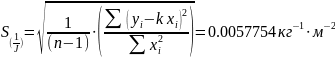
Для нахождения случайной ошибки косвенных измерений следует пользоваться формулами:
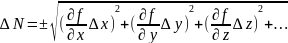
Или
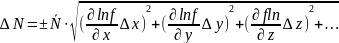 (4)
(4)
где Δx, Δy, Δz, ... – доверительные интервалы при заданных доверительных вероятностях (надежностях) для аргументов x, y, z.
По формуле (4) имеем:
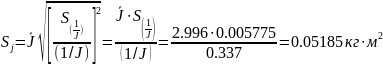
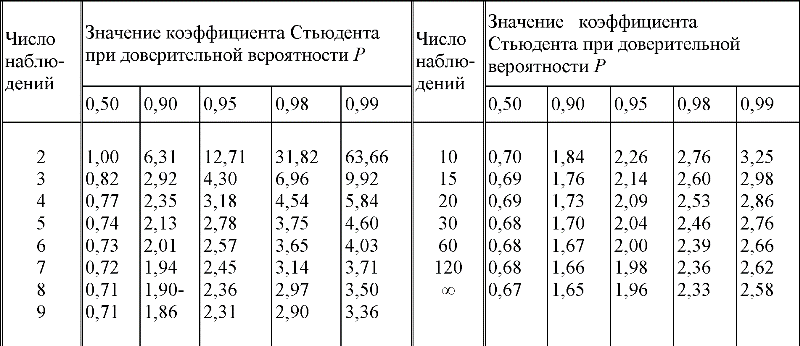
Задавшись надежностью P = 0.95 , по таблице коэффициентов Стьюдента для n = 5, находим t = 2.78 и определяем абсолютную ошибку:
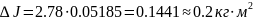
Результаты запишем в виде:
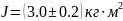
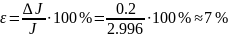
Задача 2.
Вычислим температурный коэффициент сопротивления металла по методу наименьших квадратов. Сопротивление зависит от температуры по линейному закону: Rt = R0(1 + α t) = R0 + R0 α t. Свободный член определяет сопротивление R0 при температуре 0° C , а угловой коэффициент – произведение температурного коэффициента α на сопротивление R0. Результаты измерений и расчетов приведены в таблице (см. таблицу 2).
Таблица 2
n |
t, c |
r, Ом |
t-¯ t |
(t-¯ t)2 |
(t-¯ t)r |
r - bt - a |
(r - bt - a)2 |
1 |
23 |
1.242 |
-62.8333 |
3948.028 |
-78.039 |
0.007673 |
|
2 |
59 |
1.326 |
-26.8333 |
720.0278 |
-35.581 |
-0.00353 |
|
3 |
84 |
1.386 |
-1.83333 |
3.361111 |
-2.541 |
-0.00965 |
|
4 |
96 |
1.417 |
10.16667 |
103.3611 |
14.40617 |
-0.01039 |
|
5 |
120 |
1.512 |
34.16667 |
1167.361 |
51.66 |
0.021141 |
|
6 |
133 |
1.520 |
47.16667 |
2224.694 |
71.69333 |
-0.00524 |
|
∑ |
515 |
8.403 |
– |
8166.833 |
21.5985 |
– |
|
∑/n |
85.83333 |
1.4005 |
– |
– |
– |
– |
– |
Решение:
Формула
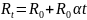 может быть представлена в виде формулы
прямой:
может быть представлена в виде формулы
прямой:
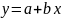 ,
где
,
где
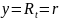 ;
;
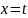 ;
;
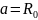 ;
;
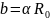 .
.Используем формулы:
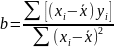 (5)
(5)
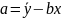 (6)
(6)
По формулам (5), (6) определяем:
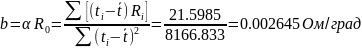
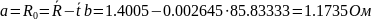
Отсюда:
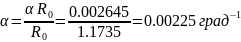
Найдем ошибку в определении α. Так как
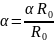 , то по формуле (4) имеем:
, то по формуле (4) имеем:
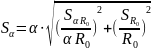
Среднеквадратичные ошибки определения a и b равны:
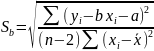 (7)
(7)
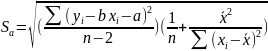 (8)
(8)
Пользуясь формулами (7), (8) имеем:
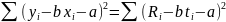
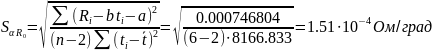
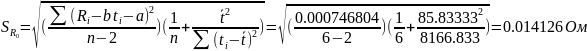
Тогда
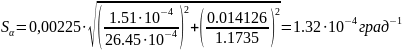
Задавшись надежностью P = 0.95, по таблице коэффициентов Стьюдента для n=6, находим t = 2.57 и определяем абсолютную ошибку:
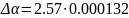 =
0.000338 град-1.
=
0.000338 град-1.
α = (23 ± 4) 10-4 град-1 при P = 0.95.
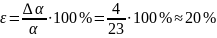
Задача 3.
Требуется определить радиус кривизны линзы по кольцам Ньютона. Измерялись радиусы колец Ньютона rm и определялись номера этих колец m. Радиусы колец Ньютона связаны с радиусом кривизны линзы R и номером кольца уравнением:
r2m = mλR - 2d0R,
где d0 – толщина зазора между линзой и плоскопараллельной пластинкой (или деформация линзы),
λ – длина волны падающего света.
Пусть λ = (600 ± 6) нм; r2m = y; m = x; λR = b; -2d0R = a, тогда уравнение примет вид y = a + bx. Результаты измерений и вычислений занесены в таблицу 3.
Таблица 3
n |
x = m |
y = r2, 10-2 мм2 |
m -¯m |
(m -¯m)2 |
(m -¯m)y |
y - bx - a, 10-4 |
(y - bx - a)2, 10-6 |
1 |
1 |
6.101 |
-2.5 |
6.25 |
|
12.01 |
1.44229 |
2 |
2 |
11.834 |
-1.5 |
2.25 |
|
-9.6 |
0.930766 |
3 |
3 |
17.808 |
-0.5 |
0.25 |
|
-7.2 |
0.519086 |
4 |
4 |
23.814 |
0.5 |
0.25 |
|
-1.6 |
0.0243955 |
5 |
5 |
29.812 |
1.5 |
2.25 |
|
3.28 |
0.107646 |
6 |
6 |
35.760 |
2.5 |
6.25 |
|
3.12 |
0.0975819 |
∑ |
21 |
125.129 |
– |
17.5 |
1.041175 |
– |
3.12176 |
∑/n |
3.5 |
20.8548333 |
– |
– |
– |
– |
– |
Решение:
Формула
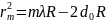 может
быть представлена в виде формулы прямой:
может
быть представлена в виде формулы прямой:
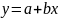 ,
где
,
где
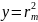 ;
;
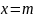 ;
;
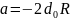 ;
;
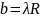 .
.Определим a и b по формулам (5), (6):
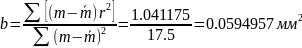
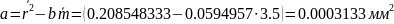
Рассчитаем среднеквадратичные ошибки для величин b и a по формулам (7), (8):
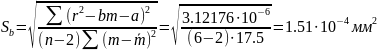
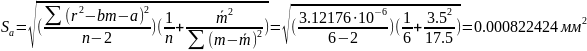
При надежности P = 0.95 по таблице коэффициентов Стьюдента для n = 6 находим t = 2.57 и определяем абсолютные ошибки:
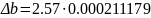 =
6·10-4
мм2;
=
6·10-4
мм2;
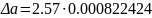 =
3· 10-3
мм2.
=
3· 10-3
мм2.
Записываем результаты:
b = (595 ± 6)·10-4 мм2 при Р = 0.95;
a = (0.3 ± 3)·10-3 мм2 при Р = 0.95.
Из полученных результатов опыта следует, что в пределах ошибки этого опыта прямая r2m = ƒ(m) проходит через начало координат, т.к. если ошибка значения какого-либо параметра окажется сравнимой или превысит значение параметра, то это означает, что скорей всего, настоящее значение этого параметра равно нулю.
В условиях данного эксперимента величина a не представляет интереса. Поэтому мы ею больше заниматься не будем.
Подсчитаем радиус кривизны линзы:
R = b / λ = 595/ 6 = 99.1 мм.
Единого мнения относительно вычисления систематической ошибки косвенных измерений нет. Однако, если исходить из определения систематической ошибки как максимально возможной ошибки, то целесообразно находить систематическую ошибку по формулам:
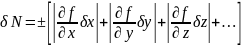
Или
 (9)
(9)
где
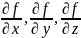 - частные производные функции
N
= ƒ(x, y, z, ...) по аргументу x, y, z..., найденные
в предположении, что все остальные
аргументы,
кроме того, по которому находится
производная, постоянные;
- частные производные функции
N
= ƒ(x, y, z, ...) по аргументу x, y, z..., найденные
в предположении, что все остальные
аргументы,
кроме того, по которому находится
производная, постоянные;
δx, δy, δz – систематические ошибки аргументов.
Так как для длины волны дана систематическая ошибка, подсчитаем и для R систематическую ошибку по формуле (9), взяв в качестве систематической ошибки величины b ее случайную ошибку Δb:
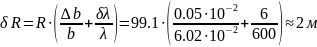
Записываем окончательный результат R = (99 ± 2) мм; ε ≈ 2% при P = 0.95.
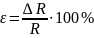
Таблица Стьюдента