
- •Приклад 1
- •Розв’язання:
- •Приклад 2
- •Приклад 3
- •Розв’язання:
- •Приклад 10
- •Розв’язок.
- •Приклад 11
- •Розв’язання:
- •Приклад 12
- •Приклад 18
- •Розв’язок.
- •Практична робота № 2
- •Завдання:
- •Теоретичні відомості
- •Приклад 1
- •Розв’язок.
- •Приклад 2
- •Розв’язок.
- •Приклад 3
- •Розв’язок.
- •Приклад 11
- •Розв’язок.
- •Теоретичні відомості
- •Приклад 1
- •Розв’язок.
- •Приклад 2
- •Розв’язок.
- •Приклад 3
- •Розв’язок.
- •Приклад 4
- •Розв’язок.
- •Приклад 5
- •Практична робота № 4
- •Теоретичні відомості
- •Контрольні запитання:
- •Приклад 1
- •Розв’язок.
- •Підставивши числові значення, знайдемо Приклад 2
- •Розв’язок.
- •Приклад 3
- •Розв’язок.
- •Приклад 4
- •Розв’язок.
- •Приклад 5
- •Рішення.
- •Приклад 6
- •Розв’язок.
- •Приклад 28
- •Розв’язання.
- •Хвилі де Бройля
- •Закон радіоактивного розпаду
- •Енергія зв’язку ядер
- •Ядерні реакції
- •Приклад 1.
- •Розв’язок.
- •Приклад 6.
- •Приклад 7.
- •Приклад 8.
- •Приклад 9.
- •Приклад 10
- •Приклад 11.
- •Розв'язання.
- •Приклад 12.
- •Розв'язання.
- •Приклад 13.
- •Розв'язання.
- •Приклад 14.
- •Розв'язання.
- •Маса нейтральних атомів (а.О.М.)
- •Основні фізичні сталі
Практична робота № 2
Тема: Розв’язування задач з молекулярної фізики
Мета: навчати розв’язувати задачі, розвивати пізнавальні можливості, працелюбство
виховувати самостійність, повагу до старших
Завдання:
Розв’язати задачу на тепловий баланс згідно свого варіанту за даними таблиці 1.
Розв’язати задачу на основні рівняння МКТ згідно свого варіанту за даними таблиці 2.
Розв’язати задачу на ізопроцеси згідно свого варіанту за даними таблиці 3.
Розв’язати задачу на закони термодинаміки згідно свого варіанту за даними таблиці 4.
Теоретичні відомості
Молекулярна фізика – розділ фізики, що вивчає будову і властивості речовини в різних агрегатних станах, процеси переходу між ними.
Термодинаміка – розділ фізики, що вивчає загальні властивості макроскопічних систем, що знаходяться в стані термодинамічної рівноваги, і процеси переходу між цими станами.
Стан
системи задається термодинамічними
параметрами
– сукупністю фізичних величин, що
характеризують властивості термодинамічної
системи. Найважливіші параметри стану
хімічно однорідної системи – об’єм
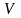 ,
тиск
,
тиск
 і температура Т.
Між цими трьома основними параметрами
стану існує зв’язок, що називається
рівнянням стану:
і температура Т.
Між цими трьома основними параметрами
стану існує зв’язок, що називається
рівнянням стану:
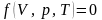 .
Стан термодинамічної системи називається
стаціонарним,
якщо значення всіх термодинамічних
параметрів системи не змінюються з
часом. Стаціонарний стан системи
називається рівноважним,
якщо його незмінність у часі не зумовлена
перебігом яких-небудь процесів у тілах,
які зовнішні відносно системи. Будь-яка
зміна в термодинамічній системі, яка
зв’язана із зміною хоча би одного з
його термодинамічних параметрів,
називається термодинамічним
процесом.
Рівноважними
називаються такі процеси,
під час яких зміна стану тіла відбувається
дуже повільно, фактично нескінченно
повільно, і при цих процесах система
проходить неперервний ряд нескінченно
близьких рівноважних термодинамічних
станів.
.
Стан термодинамічної системи називається
стаціонарним,
якщо значення всіх термодинамічних
параметрів системи не змінюються з
часом. Стаціонарний стан системи
називається рівноважним,
якщо його незмінність у часі не зумовлена
перебігом яких-небудь процесів у тілах,
які зовнішні відносно системи. Будь-яка
зміна в термодинамічній системі, яка
зв’язана із зміною хоча би одного з
його термодинамічних параметрів,
називається термодинамічним
процесом.
Рівноважними
називаються такі процеси,
під час яких зміна стану тіла відбувається
дуже повільно, фактично нескінченно
повільно, і при цих процесах система
проходить неперервний ряд нескінченно
близьких рівноважних термодинамічних
станів.
Ізопроцесами
в газах називаються процеси, при яких
один із основних параметрів стану
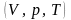 зберігається сталим.
зберігається сталим.
Закон
Бойля-Маріотта:
для даної маси газу при сталій температурі
добуток тиску газу на його об’єм є
величина стала: або
або
 .
.
Процес, що протікає при сталій температурі, називається ізотермічним.
Закон Гей-Люсаака: об’єм даної маси газу при сталому тиску змінюється лінійно з температурою:
 ,
де
,
де
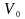 - об’єм при 0°С,
t
– температура за шкалою Цельсія,
- об’єм при 0°С,
t
– температура за шкалою Цельсія,
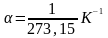 - коефіцієнт.
- коефіцієнт.
Процес,
що протікає при сталому тиску, називається
ізобарним:
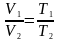 і
і
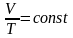 .
.
Закон
Шарля: тиск
даної маси газу при сталому об’ємі
змінюється лінійно з температурою: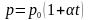
де
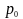 - тиск газу при 0°С.
- тиск газу при 0°С.
Процес,
який протікає при сталому об’ємі,
називається ізохорним:
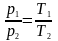 і
і
 .
.
Один
моль –
кількість речовини, яка вміщує стільки
структурних елементів, скільки є атомів
у 0,012 кг
ізотопу вуглецю
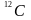 .
В одному молі різних речовин міститься
одна і та ж число молекул, яка називається
сталою
Авогадро:
.
В одному молі різних речовин міститься
одна і та ж число молекул, яка називається
сталою
Авогадро: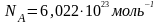 .
.
Закон Авогадро: молі різних газів при однакових температурі і тиску займають однакові об’єми.
При
нормальних умовах (Т=273,15 K,
р=1,0132·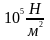 )
один моль будь-якого газу займає об’єм
22,415
)
один моль будь-якого газу займає об’єм
22,415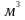 .
.
Закон Дальтона тиск суміші ідеальних газів дорівнює сумі парціальних тисків її компонент.
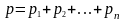 ,
де
,
де
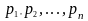 парціальні тиски – це тиск компоненти
газу коли б він один займав увесь об’єм,
який займає вся суміш.
парціальні тиски – це тиск компоненти
газу коли б він один займав увесь об’єм,
який займає вся суміш.
Рівняння
Клапейрона:
для деякої маси газу при довільній зміні
об’єму й температури тиск змінюватиметься
так, що відношення добутку тиску на
об’єм до абсолютної температури
дорівнюватиме деякій сталій величині: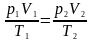 і
і
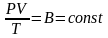 .
.
Рівняння
Клапейрона-Менделєєва: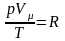 де
де
 об’єм моля газу (молярний об’єм),
об’єм моля газу (молярний об’єм),
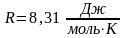 – універсальна газова стала. Для
довільної маси газу m
рівняння Клапейрона-Менделєєва має
такий вигляд:
– універсальна газова стала. Для
довільної маси газу m
рівняння Клапейрона-Менделєєва має
такий вигляд:
 ,
,
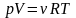 ,де
μ
– молярна маса газу, ν
– число молів газу.
,де
μ
– молярна маса газу, ν
– число молів газу.
Величина
 називається
середньою
квадратичною швидкістю.
називається
середньою
квадратичною швидкістю.
В
результаті тиск газу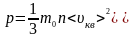 -
основне
рівнянням МКТ ідеального газу для тиску.
-
основне
рівнянням МКТ ідеального газу для тиску.
Отриману
формулу перепишемо у вигляді: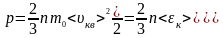 ,
,
де
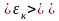 – середня кінетична енергія поступального
руху однієї молекули газу.
– середня кінетична енергія поступального
руху однієї молекули газу.
Тиск ідеального газу дорівнює двом третинам середньої кінетичної енергії молекул одиниці об’єму газу.
Густина
газу
 ,
то тиск ідеального газу
,
то тиск ідеального газу .
Звідси
.
Звідси
 .
.
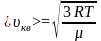 ,
,
 ,
,
 ,
де
-
стала Больцмана, то
,
де
-
стала Больцмана, то
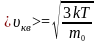
З
рівняння Клапейрона-Менделєєва
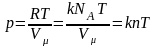 .
.
Середня
кінетична енергія поступального руху
молекул ідеального газу залежить тільки
від його абсолютної температури,
прямо пропорційна до
Т:
 .
.
Абсолютна температура є мірою середньої кінетичної енергії поступального руху молекул.
Середня арифметична
швидкість молекул
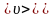 визначається за формулою
визначається за формулою .
.
Найімовірніша
швидкість
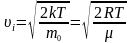 .
.
Закон Больцмана
про рівномірний розподіл енергій за
ступенями вільності молекул:
для
статистичної системи, що перебуває у
стані термодинамічної рівноваги, на
кожний поступальний і обертальний
ступінь вільності припадає в середньому
кінетична енергія, що дорівнює
 ,
а на кожний коливальний ступінь вільності
– в середньому енергія
,
а на кожний коливальний ступінь вільності
– в середньому енергія
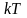 .
Середня енергія молекули
.
Середня енергія молекули
 ,
де
,
де
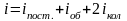 .
.
Важливою характеристикою термодинамічної системи є її внутрішня енергія U – енергія хаотичного руху мікрочастинок системи (молекул, атомів, електронів, ядер і тощо) і енергія взаємодії цих частинок.
Внутрішня
енергія
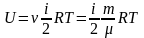 .
.
 - рівняння першого
закону термодинаміки:
теплота, надана
системі, витрачається на збільшення її
внутрішньої енергії і на виконання
системою роботи проти зовнішніх сил.
- рівняння першого
закону термодинаміки:
теплота, надана
системі, витрачається на збільшення її
внутрішньої енергії і на виконання
системою роботи проти зовнішніх сил.
Вираз для першого закону термодинаміки для нескінченно малої зміни стану системи матиме вигляд:
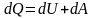 або в коректнішій
формі
або в коректнішій
формі
 ,
де
,
де
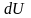 – нескінченно мала зміна внутрішньої
енергії системи,
– нескінченно мала зміна внутрішньої
енергії системи,
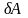 – нескінченно мала робота,
– нескінченно мала робота,
 – нескінченно мала кількість теплоти.
У цьому виразі
є повним диференціалом, а
і
не є повними диференціалами, а функціоналами
і залежать від вигляду функції, що описує
перехід з одного стану в другий.
– нескінченно мала кількість теплоти.
У цьому виразі
є повним диференціалом, а
і
не є повними диференціалами, а функціоналами
і залежать від вигляду функції, що описує
перехід з одного стану в другий.
Повну
роботу A,
яка виконана газом при зміні його об’єму
від
 до
до
 , знайдемо інтегруванням:
, знайдемо інтегруванням: Теплоємністю
тіла
називається фізична величина, яка
чисельно дорівнює кількості теплоти,
яку потрібно надати тілу, щоб підвищити
його температуру на один кельвін:
Теплоємністю
тіла
називається фізична величина, яка
чисельно дорівнює кількості теплоти,
яку потрібно надати тілу, щоб підвищити
його температуру на один кельвін: .
Значення
.
Значення
 залежить від маси тіла, його хімічного
складу, термодинамічного стану i виду
процесу зміни стану тіла, в якому
надходить теплота
.
залежить від маси тіла, його хімічного
складу, термодинамічного стану i виду
процесу зміни стану тіла, в якому
надходить теплота
.
Питомою
теплоємністю
c називається фізична величина, що
чисельно дорівнює кількості теплоти,
яку слід надати одиниці маси цієї
речовини для підвищення її температури
на
 :
: .
.
Молярною
теплоємністю
C називається фізична величина, яка
числово дорівнює кількості теплоти,
яку треба надати одному молю речовини
для підвищення його температури на
: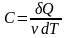 ,
де
,
де
 – кількість молей газу. Між молярною
теплоємністю
– кількість молей газу. Між молярною
теплоємністю
 і питомою теплоємністю
і питомою теплоємністю
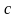 існує співвідношення:
існує співвідношення:
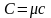 .
.
Оскільки
величина теплоємності газу залежить
від умов, при яких йому надається
кількість теплоти, то, зокрема, розрізняють
теплоємність при сталому об’ємі
 і теплоємність при сталому тиску
і теплоємність при сталому тиску
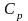 .
В першому випадку нагрівання газу
відбувається при сталому об’ємі, а в
другому – при сталому тиску. Якщо
нагрівають газ, то згідно з першим
законом термодинаміки
,
а для одного моля газу
.
В першому випадку нагрівання газу
відбувається при сталому об’ємі, а в
другому – при сталому тиску. Якщо
нагрівають газ, то згідно з першим
законом термодинаміки
,
а для одного моля газу
 .
.
Якщо
газ нагрівається при сталому об’ємі,
то надана газу теплота йде лише на
збільшення його внутрішньої енергії: .
Якщо газ нагрівається при сталому тиску,
то
.
Якщо газ нагрівається при сталому тиску,
то
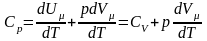 .
.
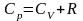 - рівняння
Майєра.
- рівняння
Майєра.
 і
і
 .
.
Застосування першого закону термодинаміки до ізопроцесів:
Ізохорний
процес
 :
δQ=dU
і
:
δQ=dU
і
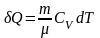 .
.
Ізобарний процес
 :
і
:
і
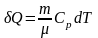 .
.
Ізотермічний процес
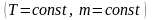 :
:
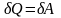 і
і
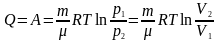 .
.
Адіабатний
– це такий процес, який відбувається
без обміну теплотою
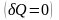 між термодинамічною системою i оточуючим
середовищем.
між термодинамічною системою i оточуючим
середовищем.
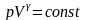 або
або
 - рівняння
Пуассона.
- рівняння
Пуассона.
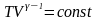 і
і
 -
рівняння
Пуассона.
-
рівняння
Пуассона.
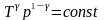 і
і
 -
рівняння
Пуассона.
-
рівняння
Пуассона.
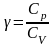 – показник адіабати,
або коефіцієнт Пуассона.
– показник адіабати,
або коефіцієнт Пуассона.
Робота
при адіабатному процесі:
 або
або
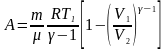 або
або
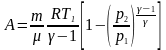 .
.
Політропним
називається процес, при якому теплоємність
тіла залишається сталою, тобто
 ,
де С=const.
,
де С=const.
 -
рівнянням політропи ідеального газу,
-
рівнянням політропи ідеального газу,
 - показник політропи.
- показник політропи.
Мінімальна
відстань, на яку зближуються при зіткненні
центри двох молекул, називається
ефективним
діаметром
d молекули.
Величина
 називається ефективним перерізом
молекули.
називається ефективним перерізом
молекули.
Середнє
число зіткнень за одиницю часу
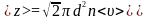 .
.
Середня
довжина вільного пробігу
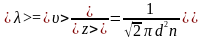 .
Оскільки
.
Оскільки
 ,
то
,
то
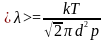 .
Закон Фіка:
маса газу M,
що переноситься завдяки дифузії
через поверхню S,
яка перпендикулярна до напрямку OX,
в якому зменшується густина, пропорційна
до розміру цієї поверхні, проміжку часу
t
перенесення і градієнта густини
.
Закон Фіка:
маса газу M,
що переноситься завдяки дифузії
через поверхню S,
яка перпендикулярна до напрямку OX,
в якому зменшується густина, пропорційна
до розміру цієї поверхні, проміжку часу
t
перенесення і градієнта густини
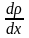 .
.
 - рівнянням дифузії,
де
- рівнянням дифузії,
де
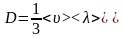 -
коефіцієнт дифузії.
-
коефіцієнт дифузії.
Закон
теплопровідності
Фур’є:
кількість теплоти Q,
яка переноситься через поверхню S,
перпендикулярну до напрямку OX,
в якому зменшується температура,
пропорційна до розміру цієї поверхні,
проміжку часу t
перенесення і градієнту температури
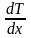 .
.
 -
-
Закон
Ньютона: сила
внутрішнього тертя, що виникає у площині
дотику двох шарів газу, що ковзають один
відносно одного, пропорційна до площі
їх дотику S
і градієнта швидкості
 .
.
 -
рівняння внутрішнього тертя. Коефіцієнт
пропорційності
-
рівняння внутрішнього тертя. Коефіцієнт
пропорційності
 називається коефіцієнтом внутрішнього
тертя або динамічною в’язкістю:
називається коефіцієнтом внутрішнього
тертя або динамічною в’язкістю:
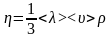 .
.
Коловим процесом (циклом) називається процес, при якому система, пройшовши через ряд станів, повертається у вихідний стан.
ККД теплового
двигуна:
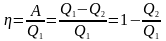 .
.
Оборотним термодинамічним процесом називається така зміна стану системи, яка, будучи проведена у зворотному напрямку, повертає її в початковий стан так, щоб система пройшла через ті самі проміжні стани, що i у прямому процесі, але у зворотній послідовності, а стан тіл поза системою залишився незмінним.
Процеси, які не задовольняють цим вимогам оборотності, називаються необоротними.
ККД
циклу Карно .
.
Відношення
кількості переданої теплоти до температури
тепловіддавача або теплоприймача
 називається зведеною
кількістю теплоти.
називається зведеною
кількістю теплоти.
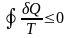 -нерівність
Клаузіуса,
причому „ = ” – для оборотних , а „ <
” – для необоротних. Функція стану,
диференціал якої є
-нерівність
Клаузіуса,
причому „ = ” – для оборотних , а „ <
” – для необоротних. Функція стану,
диференціал якої є
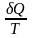 ,
називається ентропією
S.
,
називається ентропією
S.
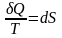 .
.
Згідно
з визначенням зміна ентропії при
оборотному процесі
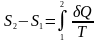 .
.
При
ізотермічному процесі
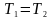 і
і
 ,при
ізохоричному процесі
,при
ізохоричному процесі
 і
і
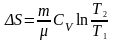 .
На нагрівання тіла від температури
.
На нагрівання тіла від температури
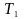 до температури
до температури
 витрачається кількість теплоти
витрачається кількість теплоти
 .
Тоді
.
Тоді
 .
.
Другий закон термодинаміки: теплота ніколи не може переходити сама собою від тіл з нижчою температурою до тіл з вищою температурою.
Третій
закон термодинаміки:
при абсолютному нулі температури
будь-які зміни стану відбуваються без
зміни ентропії: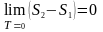 .
.
Рівняння
Ван-дер-Ваальса: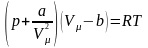 .
.
Для
довільної маси m
газу
 .
.
 ,
,
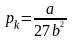 ,
,
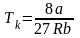 .
.
Висота
підняття рідини в капілярі
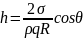 ,
,
де

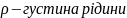 ,
,

