
- •Приклад 1
- •Розв’язання:
- •Приклад 2
- •Приклад 3
- •Розв’язання:
- •Приклад 10
- •Розв’язок.
- •Приклад 11
- •Розв’язання:
- •Приклад 12
- •Приклад 18
- •Розв’язок.
- •Практична робота № 2
- •Завдання:
- •Теоретичні відомості
- •Приклад 1
- •Розв’язок.
- •Приклад 2
- •Розв’язок.
- •Приклад 3
- •Розв’язок.
- •Приклад 11
- •Розв’язок.
- •Теоретичні відомості
- •Приклад 1
- •Розв’язок.
- •Приклад 2
- •Розв’язок.
- •Приклад 3
- •Розв’язок.
- •Приклад 4
- •Розв’язок.
- •Приклад 5
- •Практична робота № 4
- •Теоретичні відомості
- •Контрольні запитання:
- •Приклад 1
- •Розв’язок.
- •Підставивши числові значення, знайдемо Приклад 2
- •Розв’язок.
- •Приклад 3
- •Розв’язок.
- •Приклад 4
- •Розв’язок.
- •Приклад 5
- •Рішення.
- •Приклад 6
- •Розв’язок.
- •Приклад 28
- •Розв’язання.
- •Хвилі де Бройля
- •Закон радіоактивного розпаду
- •Енергія зв’язку ядер
- •Ядерні реакції
- •Приклад 1.
- •Розв’язок.
- •Приклад 6.
- •Приклад 7.
- •Приклад 8.
- •Приклад 9.
- •Приклад 10
- •Приклад 11.
- •Розв'язання.
- •Приклад 12.
- •Розв'язання.
- •Приклад 13.
- •Розв'язання.
- •Приклад 14.
- •Розв'язання.
- •Маса нейтральних атомів (а.О.М.)
- •Основні фізичні сталі
Приклад 18
Точка здійснює гармонійні коливання з частотою = 10 Гц. В момент, прийнятий за початковий, точка мала максимальне зміщення хmax = 1 мм. Написати рівняння коливань точки і накреслити їх графік.
Розв’язок.
Рівняння коливань точки можна записати у вигляді х = Аsin (t + 1), (1) або х = Аcos (t + 2), (2)
де А – амплітуда коливань; – циклічна частота; t – час; 1 і 2 – початкові фази.
За визначенням, амплітуда коливань А = хmax. (3)
Циклічна частота пов’язана з частотою співвідношенням = 2. (4)
Початкова
фаза коливань залежить від форми запису.
Якщо використати форму (1), то початкову
фазу можна визначити із умови: в момент
t
= 0
xmax
= Asin
1,
звідки
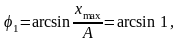 або
або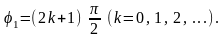 Зміна фази
на 2
не змінює стану коливального руху, тому
можна прийняти
Зміна фази
на 2
не змінює стану коливального руху, тому
можна прийняти
1
=
/ 2. (5) У випадку другої форми запису
отримуємо
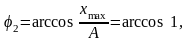
або 2 = 2 k (k = 0, 1, 2, 3, …). По тим самим міркуванням, що і в першому випадку, знаходимо
2
= 0. (6) З урахуванням рівнянь (3) – (6)
рівняння коливань будуть мати вид:
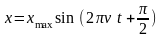
або x = xmax cos 2 t, де хmax = 1 мм = 10-3 м; = 10 Гц.
Графік відповідного гармонічного коливання приведений на рис. 4.

Рисунок 4.
Приклад 19
Визначити повну
механічну енергію матеріальної точки
масою m,
що коливається по закону x=Acos(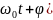 .
.
Розв’язок.
Дано:

Приклад 20
Пружина має жорсткість k = 25Н/м. Визначити, тіло якої маси m повинно бути підвішено до пружини, щоб за 1хв. Відбулося 25 коливань.
Розв’язок.
Д
ано:
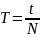 ,
,

k
= 25Н/м

t
= 1хв
= 60c
Підставивши
дані отримаємо

N = 25
m - ?
Приклад 21
Визначити довжину математичного маятника який за час 60с робить 25 коливань.
Р озв’язок.
Дано:
,
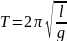
t
= 1хв
= 60c

N = 25
Підставивши
дані отримаємо

l - ?
Приклад 22
Два однаково направлені гармонічні коливання з амплітудами А1 = 4см А2 = 8см мають різницю фаз φ = 45°. Визначити амплітуду результуючого коливання, якщо їх періоди однакові.
Розв’язок.
Дано:

Підставивши дані отримаємо А = … = 11,2см.
Приклад 23
Період затухаючих коливань Т = 1с, логарифмічний декремент затухання θ = 0,3, початкова фаза дорівнює нулю. Зміщення точки при t = 2Т складає 5см. Записати рівняння цього коливання.
Р озв’язок.
Дано:


Підставивши
дані отримаємо
![]()
Приклад 24
Накладаються
два однаково направлені гармонічні
коливання, що задані рівняннями
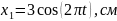 і
і
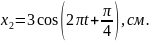 Визначити амплітуду результуючого
коливання та початкову фазу. Записати
рівняння результуючого коливання і
побудувати векторну діаграму додавання
амплітуд.
Визначити амплітуду результуючого
коливання та початкову фазу. Записати
рівняння результуючого коливання і
побудувати векторну діаграму додавання
амплітуд.
Розв’язок.
Дано:

![]()
Таблиця 1
Варіант |
Умови задач |
1 |
Визначити середню швидкість автомобіля, якщо першу половину шляху він рухався зі швидкістю 60км/год, а другу половину шляху зі швидкістю 40км/год. |
2 |
Визначити середню швидкість автомобіля, якщо першу половину часу він рухався зі швидкістю 60км/год, а другу половину часу зі швидкістю 40км/год. |
3 |
Визначити швидкість автомобіля, який за 3 год проїхав 105км. |
4 |
Визначити за який час автомобіль проїде відстань 210км, якщо його швидкість 35км/год. |
5 |
Яку відстань проїде автомобіль за час 3,5год, якщо його швидкість 62км/год. |
6 |
Побудувати графік швидкості тіла, що задане рівнянням руху х =2+5*t. |
7 |
Першу третину часу автомобіль рухався зі швидкістю 60км/год, другу третину часу зі швидкістю 80км/год, а решту зі швидкістю 85км/год. |
8 |
Автомобіль перші 90км рухався зі швидкістю 60км/год, наступні 60км проїхав за 1год, а решту шляху він проїхав за 2,5 год зі швидкістю 70км/год. Визначити середню швидкість. |
9 |
Орел, побачивши на землі мишу, починає знижуватись з швидкістю 20 м/c, рухаючись під кутом =450 до поверхні землі. Знайдіть швидкість, з якою рухається тінь орла по землі. Поверхню землі вважайте горизонтальною. |
10 |
Швидкість течії річки 3км/год, а швидкість руху човна відносно води 6км/год. Визначити, під яким кутом відносно берегу повинен пливти човен, щоб перпендикулярно перепливти річку. |
11 |
Швидкість течії річки 2км/год, а швидкість руху човна в стоячій воді 8км/год. Визначити, за який час човен пропливе відстань 60км від А до В та повернеться назад. |
12 |
Швидкість човна за течією річки 12км/год, а швидкість руху човна проти течії річки 8км/год. Визначити швидкість течії річки та власну швидкість човна( в стоячій воді). |
13 |
Швидкість людини, що рухається в потязі 5км/год, а швидкість самого потяга 65км/год. Визначити відносну швидкість людини відносно Землі. Розглянути всі можливі випадки. |
14 |
Дві матеріальні точки рухаються із швидкостями 3м/с та 4м/с перпендикулярно одна до одної. Визначити швидкість однієї точки відносно іншої. |
15 |
Які із наведених залежностей описують рівномірний рух: а) х=2-t2; b) x = 2 – 4*t; c) V= 4 - 2*t. |
16 |
Автомобіль перші 60км рухався зі швидкістю 60км/год, наступні 90км проїхав за 1год, а решту шляху він проїхав за 2,5 год зі швидкістю 70км/год. Визначити середню швидкість. |
17 |
Велосипедист рухається зі швидкістю 20км/год, а пішохід рухається зі швидкістю 4км/год. Визначити відносну швидкість велосипедиста відносно пішохода. Розглянути два випадки. |
18 |
Визначити середню швидкість автомобіля, якщо першу половину шляху він рухався зі швидкістю 90км/год, а другу половину шляху зі швидкістю 30км/год. |
19 |
Орел, побачивши на землі мишу, починає знижуватись з швидкістю 15м/c, рухаючись під кутом =600 до поверхні землі. Знайдіть швидкість, з якою рухається тінь орла по землі. Поверхню землі вважайте горизонтальною. |
20 |
Швидкість течії річки 2км/год, а швидкість руху човна відносно води 4км/год. Визначити, під яким кутом відносно берегу повинен пливти човен, щоб перпендикулярно перепливти річку. |
21 |
Визначити за який час автомобіль проїде відстань 420км, якщо його швидкість 35км/год. |
22 |
Швидкість човна за течією річки 13км/год, а швидкість руху човна проти течії річки 7км/год. Визначити швидкість течії річки та власну швидкість човна( в стоячій воді). |
23 |
Побудувати графік швидкості тіла, що задане рівнянням руху х = 3-4*t. |
24 |
Першу третину часу автомобіль рухався зі швидкістю 60км/год, другу третину часу зі швидкістю 80км/год, а решту зі швидкістю 85км/год. Визначити середню швидкість. |
25 |
Лисиця, що біжить зі швидкістю 24 м/с наздоганяє зайця, що біжить зі швидкістю 21 м/с. Відстань до заячої нори 110 м. Чи встигне заєць сховатись від лисиці? Початкова відстань між лисицею і зайцем 15 м. |
26 |
Швидкість течії річки 3км/год, а швидкість руху човна в стоячій воді 9км/год. Визначити, за який час човен пропливе відстань 72км від А до В та повернеться назад. |
27 |
Визначити середню швидкість автомобіля, якщо першу половину шляху він рухався зі швидкістю 60км/год, а другу половину шляху зі швидкістю 100км/год. |
28 |
Дві матеріальні точки рухаються із швидкостями 6м/с та 8м/с перпендикулярно одна до одної. Визначити швидкість однієї точки відносно іншої. |
29 |
Визначити швидкість автомобіля який за 5 год проїхав 155км. |
30 |
Швидкість течії річки 5км/год, а швидкість руху човна відносно води 7км/год. Визначити, під яким кутом відносно берегу повинен пливти човен, щоб перпендикулярно перепливти річку. |
31 |
Велосипедист рухається зі швидкістю 25км/год, а пішохід рухається зі швидкістю 5км/год. Визначити відносну швидкість велосипедиста відносно пішохода. Розглянути два випадки. |
32 |
Побудувати графік швидкості тіла, що задане рівнянням руху х = 2 - 2*t. |
33 |
Першу третину часу автомобіль рухався зі швидкістю 76км/год, другу третину часу зі швидкістю 80км/год, а решту зі швидкістю 87км/год. Визначити середню швидкість. |
34 |
Автомобіль перші 75км рухався зі швидкістю 50км/год, наступні 65км проїхав за 1год, а решту шляху він проїхав за 2,5 год зі швидкістю 70км/год. Визначити середню швидкість. |
35 |
Швидкість течії річки 2км/год, а швидкість руху човна в стоячій воді 10км/год. Визначити, за який час човен пропливе відстань 48км від А до В та повернеться назад. |
Таблиця 2
Варіант |
Умови задач |
1 |
Рівняння руху матеріальної точки вздовж осі має вид х = А + Вt + Ct3, де А = 3м, В = 1м/с, С = – 2,5м/с3. Знайти координату х, швидкість υ та прискорення а в момент часу t = 6 с. |
2 |
Тіло обертається навколо нерухомої осі за законом = А + Вt + Сt2, де А = 6рад, В = 10рад/с, С = -3рад/с2. Знайти повне прискорення точки, яка знаходиться на відстані r = 0,2м від осі обертання, на момент часу t = 3с. |
3 |
Камінь вільно падає в шахту з водою. Через 10с чутно сплеск води. Визначте глибину шахти, якщо швидкість звуку 330м/с. |
4 |
Тіло кидають вертикально вверх зі швидкістю 50м/с. Визначити максимальну висоту підйому та час підйому. |
5 |
Тіло кинуто під кутом 30° до горизонту з початковою швидкістю 50м/с. Визначити висоту підйому, дальність польоту та час польоту. |
6 |
Автомобіль, рухаючись зі швидкістю 72км/год., починає різко гальмувати і зупиняється. Визначити гальмівний шлях та час гальмування. |
7 |
Початкова швидкість тіла 20м/с, кінцева швидкість 10м/с. Визначити пройдений шлях за 2с. |
8 |
Визначити повне прискорення диску радіусом 30см, що обертається з кутовою швидкістю 10рад/с та має кутове прискорення 2рад/с2. |
9 |
За
графіком залежності швидкості тіла
від часу накреслити графіки зміни
прискорення а(t)
і
координати
x(t).
Визначити графічно повний шлях S,
який
пройшло тіло за цей час. Початкова
координата 0м.
|
10 |
Рівняння руху матеріальної точки вздовж осі має вид х = А + Вt + Ct3, де А = -4м, В = -21м/с, С =5м/с3. Знайти координату х, швидкість υ та прискорення а в момент часу t = 2 с. |
11 |
Тіло обертається навколо нерухомої осі за законом = А + Вt + Сt2, де А = 9рад, В = 20рад/с, С = -4рад/с2. Знайти повне прискорення точки, яка знаходиться на відстані r = 0,15м від осі обертання, на момент часу t = 5с. |
12 |
Камінь вільно падає в шахту з водою. Через 3с чутно сплеск води. Визначте глибину шахти, якщо швидкість звуку 330м/с. |
13 |
Тіло кидають вертикально вверх зі швидкістю 70м/с. Визначити максимальну висоту підйому та час підйому. |
14 |
Тіло кинуто під кутом 30° до горизонту з початковою швидкістю 70м/с. Визначити висоту підйому, дальність польоту та час польоту. |
15 |
Автомобіль, рухаючись зі швидкістю 25 м/с, починає різко гальмувати і зупиняється. Визначити гальмівний шлях та час гальмування. |
16 |
Початкова швидкість тіла 22м/с, кінцева швидкість 10м/с. Визначити пройдений шлях за 3с. |
17 |
Визначити повне прискорення диску радіусом 50см, що обертається з кутовою швидкістю 2рад/с та має кутове прискорення 4рад/с2. |
18 |
За
графіком залежності швидкості тіла
від часу накреслити графіки зміни
прискорення а(t)
і
координати
x(t).
Визначити графічно повний шлях S,
який
пройшло тіло за цей час. Початкова
координата 0м.
|
19 |
Тіло починає обертатися з частотою 5Гц та кутовим прискоренням 0,5рад/с2. Визначити скільки повних обертів зробить тіло за 10с. |
20 |
Рівняння руху матеріальної точки вздовж осі має вид х = А + Вt + Ct3, де А = -9 м, В = 3м/с, С = – 2 м/с3. Знайти координату х, швидкість υ та прискорення а в момент часу t = 5с. |
21 |
Тіло обертається навколо нерухомої осі за законом = А + Вt + Сt2, де А = -6рад, В = -8рад/с, С = 1рад/с2. Знайти повне прискорення точки, яка знаходиться на відстані r = 0,1м від осі обертання, на момент часу t = 6с. |
22 |
Камінь вільно падає в шахту з водою. Через 4с чутно сплеск води. Визначте глибину шахти, якщо швидкість звуку 330м/с. |
23 |
Тіло кидають вертикально вверх зі швидкістю 60м/с. Визначити максимальну висоту підйому та час підйому. |
24 |
Тіло кинуто під кутом 45° до горизонту з початковою швидкістю 30м/с. Визначити висоту підйому, дальність польоту та час польоту. |
25 |
Автомобіль, рухаючись зі швидкістю 36км/год., починає різко гальмувати і зупиняється. Визначити гальмівний шлях та час гальмування. |
26 |
Початкова швидкість тіла 16м/с, кінцева швидкість 8м/с. Визначити пройдений шлях за 4с. |
27 |
Визначити повне прискорення диску радіусом 10см, що обертається з кутовою швидкістю 9рад/с та має кутове прискорення 3рад/с2. |
28 |
Тіло починає обертатися з частотою 6Гц та кутовим прискоренням 1,5рад/с2. Визначити скільки повних обертів зробить тіло за 8с. |
29 |
Визначити кутове прискорення тіла, якщо за час 5с частота обертання збільшилася від 2Гц до 12Гц. |
30 |
Рівняння руху матеріальної точки вздовж осі має вид х = А + Вt + Ct3, де А = 8 м, В = 4 м/с, С = – 2,5 м/с3. Знайти координату х, швидкість υ та прискорення а в момент часу t = 4 с. |
31 |
Тіло обертається навколо нерухомої осі за законом = А + Вt + Сt2, де А = -8рад, В = 6рад/с, С = -2рад/с2. Знайти повне прискорення точки, яка знаходиться на відстані r = 0,25м від осі обертання, на момент часу t = 5с. |
32 |
Камінь вільно падає в шахту з водою. Через 5с чутно сплеск води. Визначте глибину шахти, якщо швидкість звуку 330м/с. |
33 |
Тіло кидають вертикально вверх зі швидкістю 20м/с. Визначити максимальну висоту підйому та час підйому. |
34 |
Тіло кинуто під кутом 60° до горизонту з початковою швидкістю 40м/с. Визначити висоту підйому, дальність польоту та час польоту. |
35 |
Автомобіль, рухаючись зі швидкістю 108км/год., починає різко гальмувати і зупиняється. Визначити гальмівний шлях та час гальмування. |
Таблиця 3
Варіант |
Умови задач |
1 |
Ящик масою m1 = 20 кг зісковзується по ідеально гладкому лотку довжиною l = 2 м на нерухомий візок з піском і застряє в ньому. Візок з піском масою m2 = 80 кг може вільно (без тертя) переміщуватись по рейках в горизонтальному напрямку. Визначити швидкість и візка з ящиком, якщо лоток нахилений під кутом = 300 до рейок. |
2 |
Платформа у вигляді суцільного диска радіусом R = 2,2м і масою m1 = 200кг обертається за інерцією навколо вертикальної осі з частотою n = 12хв-1. В центрі платформи стоїть людина масою m2 = 75кг. Яку лінійну швидкість відносно підлоги приміщення буде мати людина, якщо вона перейде на край платформи? |
3 |
У дерев'яну кулю масою m1 = 9кг яка підвішена на нитці довжиною L = 2м влучає куля масою m2 = 3г, яка летить горизонтально. З якою швидкістю летіла куля, якщо нитка відхилилась від вертикалі на кут =4°? Розміром кулі знехтувати. Удар вважати прямим, центральним. |
4 |
Зі ствола автоматичного пістолета вилетіла куля масою m1 = 5г зі швидкістю υ = 400м/с. Затвор пістолета масою т2 = 200г притискається до ствола пружиною, жорсткість якої k = 24кН/м. На яку відстань відійде затвор після пострілу? Вважати, що пістолет жорстко закріплений. |
5 |
Пружина жорсткістю k = 400Н/м стиснута силою F = 200Н. Визначити роботу А зовнішньої сили, додатково стискаючої цю пружину ще на Δl = 2см. |
6 |
На деяке точкове тіло діють три сили, які лежать в одній площині і модулі яких відповідно рівні F1= 30H, F2= 20H, F3= 50H. Кут між векторами сил та дорівнює 450, а між векторами та - 1350. Знайдіть величину і напрям вектора рівнодійної. |
7 |
По круговій орбіті навколо Землі обертається супутник з періодом Т = 115 хв. Визначити висоту супутника. |
8 |
Колесо радіусом 50см і масою 4кг скочується без тертя з похилої площини довжиною 8м і кутом нахилу 10°. Визначити момент інерції колеса, якщо його швидкість в кінці спуску 3м/с. |
9 |
Через нерухомий блок, розміщений у вершині похилої площини з кутом нахилу 40°, перекинуто нерозтяжну нитку, до кінців якої прив’язані вантажі масами 250г та 200г. Нехтуючи силами тертя, визначити прискорення тіл, якщо опускається вниз тіло з меншою масою. |
10 |
Ящик масою m1 = 15 кг зісковзується по ідеально гладкому лотку довжиною l = 5 м на нерухомий візок з піском і застряє в ньому. Візок з піском масою m2 = 90 кг може вільно (без тертя) переміщуватись по рейках в горизонтальному напрямку. Визначити швидкість и візка з ящиком, якщо лоток нахилений під кутом = 300 до рейок. |
11 |
Платформа у вигляді суцільного диска радіусом R = 2,3м і масою m1 = 170кг обертається за інерцією навколо вертикальної осі з частотою n = 13хв-1. В центрі платформи стоїть людина масою m2 = 75кг. Яку лінійну швидкість відносно підлоги приміщення буде мати людина, якщо вона перейде на край платформи? |
12 |
У дерев'яну кулю масою m1 = 10кг яка підвішена на нитці довжиною L= 2м влучає куля масою m2 = 4г, яка летить горизонтально. З якою швидкістю летіла куля, якщо нитка відхилилась від вертикалі на кут =2°? Розміром кулі знехтувати. Удар вважати прямим, центральним. |
13 |
Зі ствола автоматичного пістолета вилетіла куля масою m1 = 6г зі швидкістю υ = 350м/с. Затвор пістолета масою т2 = 150г притискається до ствола пружиною, жорсткість якої k = 23кН/м. На яку відстань відійде затвор після пострілу? Вважати, що пістолет жорстко закріплений. |
14 |
Нехтуючи в’язкістю рідини, визначити швидкість витікання рідини із малого отвору в стінці посудини, якщо висота рівня рідини над отвором становить 1,8м. |
15 |
Дві пружини жорсткістю k1 = 0,5кН/м і k2 = 1,5кН/м закріплені паралельно. Визначити потенціальну енергію П даної системи при абсолютній деформації L = 5см. |
16 |
Супутник обертається навколо Землі за круговою орбітою на висоті h = 420 км. Визначити період обертання супутника. |
17 |
На деяке точкове тіло діють три сили, які лежать в одній площині і модулі яких відповідно рівні F1= 40H, F2= 60H, F3= 90H. Кут між векторами сил та дорівнює 600, а між векторами та - 1600. Знайдіть величину і напрям вектора рівнодійної. |
18 |
Через блок у вигляді суцільного диска, який має масу m = 200г (рис. 3), перекинута тонка, гнучка нитка, до кінців якої підвішені вантажі з масами m1 = 170г і m2 = 310г. З яким прискоренням будуть рухатись вантажі самі по собі? Тертям і масою нитки знехтувати. |
19 |
Колесо радіусом 40см і масою 3кг скочується без тертя з похилої площини довжиною 6м і кутом нахилу 40°. Визначити момент інерції колеса, якщо його швидкість в кінці спуску 8м/с. |
20 |
Ящик масою m1 = 30 кг зісковзується по ідеально гладкому лотку довжиною l = 3 м на нерухомий візок з піском і застряє в ньому. Візок з піском масою m2 = 100 кг може вільно (без тертя) переміщуватись по рейках в горизонтальному напрямку. Визначити швидкість и візка з ящиком, якщо лоток нахилений під кутом = 600 до рейок. |
21 |
Платформа у вигляді суцільного диска радіусом R = 1,8м і масою m1 = 170кг обертається за інерцією навколо вертикальної осі з частотою n = 11хв-1. В центрі платформи стоїть людина масою m2 = 80кг. Яку лінійну швидкість відносно підлоги приміщення буде мати людина, якщо вона перейде на край платформи? |
22 |
У дерев'яну кулю масою m1 =11кг яка підвішена на нитці довжиною L = 1,9м влучає куля масою m2 = 4г, яка летить горизонтально. З якою швидкістю летіла куля, якщо нитка відхилилась від вертикалі на кут =4°? Розміром кулі знехтувати. Удар вважати прямим, центральним. |
23 |
Зі ствола автоматичного пістолета вилетіла куля масою m1 = 7г зі швидкістю υ = 350м/с. Затвор пістолета масою т2 = 170г притискається до ствола пружиною, жорсткість якої k = 22кН/м. На яку відстань відійде затвор після пострілу? Вважати, що пістолет жорстко закріплений. |
24 |
Горизонтальною трубою змінного перерізу тече вода. Площа поперечних перерізів труби в різних місцях 11см2 і 25см2. Різниця рівнів води в вертикальних трубках однакового перерізу складає 28см. Визначити об’єм води, що протікає за 1с через поперечний переріз труби. |
25 |
Налетівши на пружинний буфер, вагон масою m = 20т, який рухався зі швидкістю υ = 0,8м/с, зупинився, стиснувши пружину на L = 10см. Знайти загальну жорсткість k пружин буфера. |
26 |
Визначити лінійну та кутову швидкості супутника Землі, який обертається по колу на висоті 1100 км. |
27 |
На деяке точкове тіло діють три сили, які лежать в одній площині і модулі яких відповідно рівні F1= 50H, F2= 20H, F3= 70H. Кут між векторами сил та дорівнює 450, а між векторами та - 1350. Знайдіть величину і напрям вектора рівнодійної. |
28 |
Колесо радіусом 30см і масою 4кг скочується без тертя з похилої площини довжиною 6м і кутом нахилу 30°. Визначити момент інерції колеса, якщо його швидкість в кінці спуску 6м/с. |
29 |
Через нерухомий блок, розміщений у вершині похилої площини з кутом нахилу 60°, перекинуто нерозтяжну нитку, до кінців якої прив’язані вантажі масами 300г та 250г. Нехтуючи силами тертя, визначити прискорення тіл, якщо опускається вниз тіло з меншою масою. |
30 |
Ящик масою m1 = 25 кг зісковзується по ідеально гладкому лотку довжиною l = 4 м на нерухомий візок з піском і застряє в ньому. Візок з піском масою m2 = 85кг може вільно (без тертя) переміщуватись по рейках в горизонтальному напрямку. Визначити швидкість и візка з ящиком, якщо лоток нахилений під кутом = 600 до рейок. |
31 |
Платформа у вигляді суцільного диска радіусом R = 1,6м і масою m1 = 160кг обертається за інерцією навколо вертикальної осі з частотою n = 14хв-1. В центрі платформи стоїть людина масою m2 = 85кг. Яку лінійну швидкість відносно підлоги приміщення буде мати людина, якщо вона перейде на край платформи? |
32 |
У дерев'яну кулю масою m1 = 12кг яка підвішена на нитці довжиною L = 1,6м влучає куля масою m2 = 5г, яка летить горизонтально. З якою швидкістю летіла куля, якщо нитка відхилилась від вертикалі на кут =5°? Розміром кулі знехтувати. Удар вважати прямим, центральним. |
33 |
Зі ствола автоматичного пістолета вилетіла куля масою m1 = 8г зі швидкістю υ = 400м/с. Затвор пістолета масою т2 = 180г притискається до ствола пружиною, жорсткість якої k = 21кН/м. На яку відстань відійде затвор після пострілу? Вважати, що пістолет жорстко закріплений. |
34 |
Пружина жорсткістю k = 550Н/м стиснута силою F = 275Н. Визначити роботу А зовнішньої сили, додатково стискаючої цю пружину ще на Δl = 2см. |
35 |
По круговій орбіті навколо Землі обертається супутник з періодом Т = 110 хв. Визначити висоту супутника. |
Таблиця 4
Варіант |
Умови задач |
1 |
Гармонічні
коливання задаються рівнянням х =
0,02cos(6πt+ 1) амплітуду коливань; 2) циклічну частоту; 3) частоту коливань; 4) період коливання. |
2 |
Точка здійснює гармонійні коливання з частотою = 20Гц. В момент, прийнятий за початковий, точка мала максимальне зміщення хmax = 2мм. Написати рівняння коливань точки і накреслити їх графік. |
3 |
Записати рівняння гармонічного коливання точки з амплітудою А=8см, якщо за t = 1хв. здійснюється N = 120 коливань і початкова фаза коливань дорівнює φ = 45°. |
4 |
Швидкість матеріальної точки, що здійснює гармонічні коливання, задається рівнянням ʋ(t) = -6sin2πt. Записати рівняння залежності зміщення цієї точки від часу. |
5 |
Визначити повну
механічну енергію матеріальної точки
масою m
= 20г, що коливається по закону x
= 10cos( |
6 |
Пружина має жорсткість k = 35Н/м. Визначити, тіло якої маси m повинно бути підвішено до пружини, щоб за 1хв. відбулося 35 коливань. |
7 |
Визначити довжину математичного маятника який за час 6хв. робить 720 коливань. |
8 |
Два однаково направлені гармонічні коливання з амплітудами А1 = 5см і А2 = 9см мають різницю фаз φ = 30°. Визначити амплітуду результуючого коливання, якщо їх періоди однакові. |
9 |
Накладаються два
однаково направлені гармонічні
коливання, що задані рівняннями
|
10 |
Період затухаючих коливань Т = 2с, логарифмічний декремент затухання θ = 0,25, початкова фаза дорівнює нулю. Зміщення точки при t = 3Т складає 7см. Записати рівняння цього коливання. |
11 |
Гармонічні
коливання задаються рівнянням х =
0,01cos(2πt+ 1) амплітуду коливань; 2) циклічну частоту; 3) частоту коливань; 4) період коливання. |
12 |
Точка здійснює гармонійні коливання з частотою = 15Гц. В момент, прийнятий за початковий, точка мала максимальне зміщення хmax = 1,5мм. Написати рівняння коливань точки і накреслити їх графік. |
13 |
Записати рівняння гармонічного коливання точки з амплітудою А=9см, якщо за t = 1хв. здійснюється N = 180 коливань і початкова фаза коливань дорівнює φ = 60°. |
14 |
Швидкість матеріальної точки, що здійснює гармонічні коливання, задається рівнянням ʋ(t) = -5cos2πt. Записати рівняння залежності зміщення цієї точки від часу. |
15 |
Визначити
повну механічну енергію матеріальної
точки масою m
= 40г, що коливається по закону x
= 40cos( |
16 |
Пружина має жорсткість k = 45Н/м. Визначити, тіло якої маси m повинно бути підвішено до пружини, щоб за 2хв. відбулося 90коливань. |
17 |
Визначити довжину математичного маятника який за час 5хв. робить 600 коливань. |
18 |
Два однаково направлені гармонічні коливання з амплітудами А1 = 7см і А2 = 9см мають різницю фаз φ = 60°. Визначити амплітуду результуючого коливання, якщо їх періоди однакові. |
19 |
Накладаються
два однаково направлені гармонічні
коливання, що задані рівняннями
|
20 |
Період затухаючих коливань Т = 1,5с, логарифмічний декремент затухання θ = 0,5, початкова фаза дорівнює нулю. Зміщення точки при t = 4Т складає 3см. Записати рівняння цього коливання. |
21 |
Гармонічні
коливання задаються рівнянням х =
0,06cos(7πt+ 1) амплітуду коливань; 2) циклічну частоту; 3) частоту коливань; 4) період коливання. |
22 |
Точка здійснює гармонійні коливання з частотою = 25Гц. В момент, прийнятий за початковий, точка мала максимальне зміщення хmax = 3мм. Написати рівняння коливань точки і накреслити їх графік. |
23 |
Записати рівняння гармонічного коливання точки з амплітудою А=7см, якщо за t = 2хв. здійснюється N = 220 коливань і початкова фаза коливань дорівнює φ = 30°. |
24 |
Швидкість матеріальної точки, що здійснює гармонічні коливання, задається рівнянням ʋ(t) = -8cos4πt. Записати рівняння залежності зміщення цієї точки від часу. |
25 |
Визначити
повну механічну енергію матеріальної
точки масою m
= 30г, що коливається по закону x
= 30cos( |
26 |
Пружина має жорсткість k = 20Н/м. Визначити, тіло якої маси m повинно бути підвішено до пружини, щоб за 3хв. відбулося 90 коливань. |
27 |
Визначити довжину математичного маятника який за час 4хв. робить 240 коливань. |
28 |
Два однаково направлені гармонічні коливання з амплітудами А1 = 6см і А2 = 10см мають різницю фаз φ = 40°. Визначити амплітуду результуючого коливання, якщо їх періоди однакові. |
29 |
Накладаються
два однаково направлені гармонічні
коливання, що задані рівняннями
|
30 |
Період затухаючих коливань Т = 2,5с, логарифмічний декремент затухання θ = 0,35, початкова фаза дорівнює 30°. Зміщення точки при t = 1/12с складає 4см. Записати рівняння цього коливання. |
31 |
Гармонічні
коливання задаються рівнянням х =
0,05cos(3πt+ 1) амплітуду коливань; 2) циклічну частоту; 3) частоту коливань; 4) період коливання. |
32 |
Точка здійснює гармонійні коливання з частотою = 5Гц. В момент, прийнятий за початковий, точка мала максимальне зміщення хmax = 0,5мм. Написати рівняння коливань точки і накреслити їх графік. |
33 |
Записати рівняння гармонічного коливання точки з амплітудою А=5см, якщо за t = 3хв. здійснюється N = 420 коливань і початкова фаза коливань дорівнює φ = 45°. |
34 |
Швидкість матеріальної точки, що здійснює гармонічні коливання, задається рівнянням ʋ(t) = -6sin3πt. Записати рівняння залежності зміщення цієї точки від часу. |
35 |
Визначити
повну механічну енергію матеріальної
точки масою m
= 50г, що коливається по закону x
= 5cos( |
Контрольні запитання:
Що таке сила?
Що таке імпульс тіла?
Що таке коливання?
Чим відрізняється шлях від переміщення?
Чи може бути прискорення від’ємним?
Що таке момент сили?
Що таке момент інерції?
Що таке момент імпульсу?
Що таке рівнозмінний рух?
Що таке рівномірний прямолінійний рух?
Що таке хвиля?
Що таке математичний маятник?
Що таке інертність?
Сформулювати 1 закон Ньютона.
Сформулювати 2 закон Ньютона.
Сформулювати 3 закон Ньютона.
Сформулювати закон збереження імпульсу.
Сформулювати закон збереження енергії.
Що таке пружинний маятник?
Які коливання називаються затухаючими?



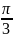 ).
Визначити:
).
Визначити:
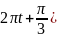 см.
см. і
і
 Визначити амплітуду результуючого
коливання та початкову фазу. Записати
рівняння результуючого коливання і
побудувати векторну діаграму додавання
амплітуд.
Визначити амплітуду результуючого
коливання та початкову фазу. Записати
рівняння результуючого коливання і
побудувати векторну діаграму додавання
амплітуд. ).
Визначити:
).
Визначити:
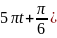 см.
см. і
і
 Визначити амплітуду результуючого
коливання та початкову фазу. Записати
рівняння результуючого коливання і
побудувати векторну діаграму додавання
амплітуд.
Визначити амплітуду результуючого
коливання та початкову фазу. Записати
рівняння результуючого коливання і
побудувати векторну діаграму додавання
амплітуд.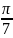 ).
Визначити:
).
Визначити: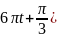 см.
см. і
і
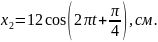 Визначити амплітуду результуючого
коливання та початкову фазу. Записати
рівняння результуючого коливання і
побудувати векторну діаграму додавання
амплітуд.
Визначити амплітуду результуючого
коливання та початкову фазу. Записати
рівняння результуючого коливання і
побудувати векторну діаграму додавання
амплітуд. ).
Визначити:
).
Визначити:
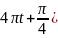 см.
см.