Приклад 12

Через блок у вигляді суцільного диска, який має масу m = 80 г (рис. 3), перекинута тонка, гнучка нитка, до кінців якої підвішені вантажі з масами m₁ = 100 г і m₂ = 200 г. З яким прискоренням будуть рухатись вантажі самі по собі? Тертям і масою нитки знехтувати.

Розв’язок.

Скористаємося основними рівняннями динаміки поступального і обертального рухів. Для цього розглянемо сили, які діють на кожний з вантажів і на блок окремо. На перший вантаж діють дві сили: сила тяжіння і сила пружності (сила натягу нитки) Спроектуємо ці сили на вісь х, яку направимо вниз, і напишемо рівняння руху (другий закон Ньютона) в координатній формі: m₁g – T₁ = -m₁a. (1)

Рівняння руху для другого вантажу запишеться аналогічно: m₂g – T₂ = -m₂a. (2)

Під дією двох моментів сил і 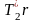відносно осі, перпендикулярної площині креслення, блок отримає кутове прискорення  ( = а / r). Згідно основного рівняння динаміки обертального руху (3)

Рисунок 3.

де 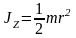– момент інерції блоку (суцільного диску) відносно до осі Z. Сила згідно третьому закону Ньютона за абсолютним значенням дорівнює силі Т₁. Відповідно сила 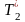за абсолютним значенням дорівнює силі Т₂. Скориставшись цим, підставимо в рівняння (3) замість і вираз для Т₁ і Т₂, які ми отримали попередньо з рівнянь (1) і (2): Після скорочення на r та перегрупування членів знайдемо прискорення, яке нас цікавить: (4)

Відношення мас в правій частині формули (4) є величина безрозмірна. Тому маси m₁, m₂ і m можна виразити в грамах, як вони надані в умові задачі. Прискорення треба виразити в одиницях СІ. Після підстановки одержимо

Приклад 13

Через нерухомий блок, розміщений у вершині похилої площини з кутом нахилу 20°, перекинуто нерозтяжну нитку, до кінців якої прив’язані вантажі масами 200г та 150г. Нехтуючи силами тертя, визначити прискорення тіл, якщо опускається вниз тіло з меншою масою.

Р озв’язок.

Дано:

α = 20°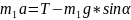

m₁ = 200г = 0,2кг

m₂ = 150г = 0,15кг м/с².

a - ?

m₂g

Приклад 14

Колесо радіусом 30см і масою 3кг скочується без тертя з похилої площини довжиною 5м і кутом нахилу 25°. Визначити момент інерції колеса, якщо його швидкість в кінці спуску 4,6м/с.

Розв’язок.

Підставивши значення отримаємо J = … = 0,259кг*м².

Приклад 15

Період обертання штучного супутника Землі дорівнює 3год. Вважаючи його орбіту коловою, визначити, на якій висоті від поверхні Землі розташований супутник.

Розв’язок.

Дано:

Підставивши дані отримаємо h = … = 4,19Мм.

Приклад 16

Нехтуючи в’язкістю рідини, визначити швидкість витікання рідини із малого отвору в стінці посудини, якщо висота рівня рідини над отвором становить 1,5м.

Розв’язок.

Дано:

Підставивши дані отримаємо ʋ = … = 5,42м/с.

Приклад 17

Горизонтальною трубою змінного перерізу тече вода. Площа поперечних перерізів труби в різних місцях 10см² і 20см². Різниця рівнів води в вертикальних трубках однакового перерізу складає 20см. Визначити об’єм води, що протікає за 1с через поперечний переріз труби.

Дано: Рівняння Бернуллі для горизонтального випадку

Підставивши дані отримаємо V = … = 2,29*10³ см³.