Приклад 1

Від двох когерентних джерел S₁ та S₂ ( = 0,8 мкм) промені падають на екран. На екрані спостерігається інтерференційна картина. Коли на шляху одного з променів перпендикулярно до нього помістили мильну плівку (n = 1,33), інтерференційна картина змінилась на протилежну. При якій найменшій товщині d_min плівки це можливо?

Розв’язок.

Зміна інтерференційної картини на протилежну означає, що та тих ділянках екрана, де спостерігались інтерференційні максимуми, стали спостерігатися інтерференційні мінімуми. Така зміна інтерференційної картини можлива при зміні оптичної різниці ходу променів на непарне число половин довжин хвиль, тобто, (1)

де ₁ – оптична різниця руху променів до внесення плівки;

₂ – оптична різниця ходу тих самих променів після внесення плівки; k = 0,  1,  2, ... .

Рисунок 2.

Найменша товщина d_min плівки відповідає k = 0. При цьому формула (1) буде мати вид

(2)

Виразимо оптичні різниці ходу ₂ та ₁. Із рис. 2 виходить: ₁ = l₁ – l₂, ₂ = [(l₁ – d_min) + nd_min] – l₂ = (l₁ – l₂) + d_min (n – 1).

Підставимо вирази ₂ та ₁ в формулу (2): (l₁ – l₂) + d_min (n – 1) - (l₁ – l₂) = 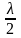, або d_min (n – 1) = . Звідси

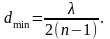
Підставивши числові значення, знайдемо Приклад 2

На дифракційну гратку у напрямку нормалі до її поверхні падає монохроматичне світло. Період гратки d = 2 мкм. Якого найбільшого порядку дифракційного максимуму надає ця гратка у випадку червоного (₁ = 0,7 мкм) та у випадку фіолетового (₂ = 0,41 мкм) світла?

Розв’язок.

На підставі відомої формули дифракційної гратки запишемо вираз порядку дифракційного максимуму: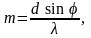 (1)

де d – період гратки; - кут між напрямком на дифракційний максимум і нормаллю до гратки;

 - довжина хвилі монохроматичного світла.

Так як sin  не може бути більшим за 1, то, як це слідує з формули (1), число m не може бути більшим d / , тобто m  d / . (2)

Підставивши у формулу (2) числові значення, знайдемо:для червоних променів m  2 / 0,7 = 2,86; для фіолетових променів m  2 / 0,41 = 4,88. Якщо враховувати, що порядок максимумів є цілим числом, то для червоного світла m_max = 2 і для фіолетового m_max = 4.

Приклад 3

Природній промінь світла падає на поліровану поверхню скляної пластини, яка розміщена в рідині. Відбитий від пластини промінь світла утворює кут  = 97⁰ з променем, який падає (рис. 3) Визначити показник заломлення n₁ рідини, якщо відбитий промінь світла максимально поляризований.

Розв’язок.

Згідно закону Брюстера, промінь світла, відбитий від діелектрика, максимально поляризований в тому випадку, якщо тангенс кута падіння чисельно дорівнює відносному показнику заломлення: tg i₁ = n₂₁, де n₂₁ – показник заломлення другого середовища (скла) відносно першого (рідини).

Відносний показник заломлення дорівнює відношенню абсолютних показників заломлення. Отже, tg i₁ = n₂ / n₁.

Так як кут падіння дорівнює куту відбиття, то і₁ =  / 2 і, tg  / 2 = n₂ / n₁ звідки

Підставивши числові значення, знайдемо

Рисунок 3.