- •Приклад 1
- •Розв’язання:
- •Приклад 2
- •Приклад 3
- •Розв’язання:
- •Приклад 10
- •Розв’язок.
- •Приклад 11
- •Розв’язання:
- •Приклад 12
- •Приклад 18
- •Розв’язок.
- •Практична робота № 2
- •Завдання:
- •Теоретичні відомості
- •Приклад 1
- •Розв’язок.
- •Приклад 2
- •Розв’язок.
- •Приклад 3
- •Розв’язок.
- •Приклад 11
- •Розв’язок.
- •Теоретичні відомості
- •Приклад 1
- •Розв’язок.
- •Приклад 2
- •Розв’язок.
- •Приклад 3
- •Розв’язок.
- •Приклад 4
- •Розв’язок.
- •Приклад 5
- •Практична робота № 4
- •Теоретичні відомості
- •Контрольні запитання:
- •Приклад 1
- •Розв’язок.
- •Підставивши числові значення, знайдемо Приклад 2
- •Розв’язок.
- •Приклад 3
- •Розв’язок.
- •Приклад 4
- •Розв’язок.
- •Приклад 5
- •Рішення.
- •Приклад 6
- •Розв’язок.
- •Приклад 28
- •Розв’язання.
- •Хвилі де Бройля
- •Закон радіоактивного розпаду
- •Енергія зв’язку ядер
- •Ядерні реакції
- •Приклад 1.
- •Розв’язок.
- •Приклад 6.
- •Приклад 7.
- •Приклад 8.
- •Приклад 9.
- •Приклад 10
- •Приклад 11.
- •Розв'язання.
- •Приклад 12.
- •Розв'язання.
- •Приклад 13.
- •Розв'язання.
- •Приклад 14.
- •Розв'язання.
- •Маса нейтральних атомів (а.О.М.)
- •Основні фізичні сталі
ЖИТОМИРСЬКИЙ АГРОТЕХНІЧНИЙ КОЛЕДЖ
ЗОШИТ
ДЛЯ ВИКОНАННЯ ПРАКТИЧНИХ РОБІТ
З ФІЗИКИ
СТУДЕНТА ГРУПИ П- 21
2015
Практична робота № 1.
Тема: Розв’язування задач з механіки.
Мета: навчати розв’язувати задачі, розвивати пізнавальні можливості, працелюбство
виховувати самостійність, повагу до старших
Завдання:
Розв’язати задачу на рівномірний рух згідно свого варіанту за даними таблиці 1.
Розв’язати задачу на рівнозмінний рух згідно свого варіанту за даними таблиці 2.
Розв’язати задачу на закони збереження та закони Ньютона згідно свого варіанту за даними таблиці 3.
Розв’язати задачу на механічні коливання та хвилі згідно свого варіанту за даними таблиці 4.
Теоретичні відомості
Механіка – розділ фізики, що вивчає механічний рух, взаємодію тіл та положення рівноваги.
Розділи механіки: кінематика, динаміка та статика.
Траєкторія – уявна лінія, що описує рух тіла.
Шлях – довжина траєкторії.
Вектор
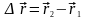 ,
проведений з початкового положення
рухомої точки в положення її в даний
момент часу, називається вектором
переміщення.
,
проведений з початкового положення
рухомої точки в положення її в даний
момент часу, називається вектором
переміщення.
Вектором
середньої швидкості
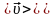 руху точки в інтервалі часу від t
до
руху точки в інтервалі часу від t
до
 називається
відношення
приросту
називається
відношення
приросту
 радіус-вектора точки за цей інтервал
часу до його величини
радіус-вектора точки за цей інтервал
часу до його величини
 :
: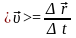 або
або
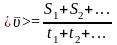
Миттєва
швидкість
 - векторна величина, яка дорівнює першій
похідній радіус-вектора рухомої точки
за часом.
- векторна величина, яка дорівнює першій
похідній радіус-вектора рухомої точки
за часом.

Вектор швидкості напрямлений вздовж дотичної до траєкторії в сторону руху.
Модуль
швидкості можна обчислити через проекції
швидкості:

Довжина
шляху, який пройдений точкою за проміжок
часу від t1
до t2,


 Середнім
прискоренням нерівномірного
руху в інтервалі часу від t
до t+t
називається вектор
Середнім
прискоренням нерівномірного
руху в інтервалі часу від t
до t+t
називається вектор
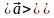 ,
який дорівнює відношенню приросту
,
який дорівнює відношенню приросту
 вектора швидкості точки до проміжку
часу t:
вектора швидкості точки до проміжку
часу t:

Вектор
збігається за напрямком з вектором
зміни швидкості
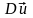 .
.
Миттєвим
прискоренням
точки в момент часу t
називають векторну величину
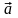 ,
яка дорівнює границі середнього
прискорення, якщо
,
яка дорівнює границі середнього
прискорення, якщо
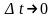 :
:
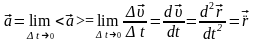 .
.
Вектор прискорення
можна зобразити у вигляді суми двох
взаємно перпендикулярних векторів:
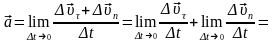

Величина
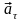 називається тангенціальним
прискоренням,
яке характеризує зміну швидкості лише
за величиною і напрямлене вздовж дотичної
до траєкторії.
називається тангенціальним
прискоренням,
яке характеризує зміну швидкості лише
за величиною і напрямлене вздовж дотичної
до траєкторії.
Числове
значення вектора
дорівнює:
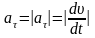 .
.
Величина
 називається вектором нормального
прискорення
і характеризує зміну швидкості лише за
напрямком. Це прискорення завжди
перпендикулярне до напрямку швидкості.
Для його обчислення припустимо, що точка
В досить близька до точки А, тому
називається вектором нормального
прискорення
і характеризує зміну швидкості лише за
напрямком. Це прискорення завжди
перпендикулярне до напрямку швидкості.
Для його обчислення припустимо, що точка
В досить близька до точки А, тому
 можна вважати дугою кола радіусом R,
при цьому за величиною ця дуга мало
відрізняється від хорди АВ. З подібності
трикутників ОАВ і BDC
отримаємо:
можна вважати дугою кола радіусом R,
при цьому за величиною ця дуга мало
відрізняється від хорди АВ. З подібності
трикутників ОАВ і BDC
отримаємо:
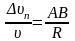 і
і
 .
Таким чином
.
Таким чином
 .
.
Напрямок
повного прискорення визначається кутом
 між векторами
і
.
З рис. 3 видно, що:
між векторами
і
.
З рис. 3 видно, що:
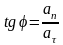 .
.
Залежність
від часу координати х будь-якої точки
має вигляд:
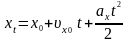 .
.
 Перший
закон Ньютона:
всяка матеріальна точка (тіло) зберігає
стан спокою або рівномірного прямолінійного
руху доти, доки дія з боку інших тіл не
змусить її змінити цей стан. Перший
закон Ньютона називають законом інерції,
а властивість тіл зберігати стан спокою
або рівномірного прямолінійного руху
без дії на них інших тіл називають
інертністю.
Системи відліку, відносно яких виконується
перший закон Ньютона, називаються
інерціальними
системами відліку.
Перший
закон Ньютона:
всяка матеріальна точка (тіло) зберігає
стан спокою або рівномірного прямолінійного
руху доти, доки дія з боку інших тіл не
змусить її змінити цей стан. Перший
закон Ньютона називають законом інерції,
а властивість тіл зберігати стан спокою
або рівномірного прямолінійного руху
без дії на них інших тіл називають
інертністю.
Системи відліку, відносно яких виконується
перший закон Ньютона, називаються
інерціальними
системами відліку.
Маса - міра інертності тіла.
С илою
називається векторна величина, що є
мірою механічної дії на тіло з боку
інших тіл, внаслідок якої тіло отримує
прискорення або змінює свою форму і
розміри.
илою
називається векторна величина, що є
мірою механічної дії на тіло з боку
інших тіл, внаслідок якої тіло отримує
прискорення або змінює свою форму і
розміри.
Другий
закон Ньютона:Прискорення,
що його набуває тіло, прямо пропорційне
до сили, яка діє на нього, і обернено
пропорційне до маси цього тіла; за
напрямком прискорення збігається із
силою:
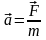 .
.
Векторна величина
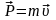 називається імпульсом
(кількістю руху) матеріальної точки.
називається імпульсом
(кількістю руху) матеріальної точки.
Третій закон
Ньютона: сили
взаємодії двох матеріальних точок в
інерціальній системі відліку однакові
за модулем, напрямлені у протилежні
сторони і діють вздовж прямої, що з’єднує
ці точки:
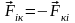 .
.
Сукупність матеріальних точок (тіл), які розглядаються як єдине ціле, називається механічною системою. Сили взаємодії між матеріальними точками механічної системи називаються внутрішніми. Сили, з якими на матеріальні точки системи діють зовнішні тіла називаються зовнішніми. Механічна система, в якій тіла взаємодіють між собою і на яку не діють зовнішні сили, називається замкненою.
Закон збереження
імпульсу:
імпульс замкненої системи зберігається,
тобто не змінюється із бігом часу:
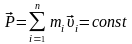 .
.
Центр мас - це геометрична точка, для якої сума добутків мас всіх матеріальних точок, що утворюють механічну систему, на їх радіус-вектори, які проведені з цієї точки, дорівнює нулю.
Центр мас механічної
системи рухається як матеріальна точка,
в якій зосереджено всю масу системи і
на яку діє сила, що дорівнює головному
вектору прикладених до системи зовнішніх
сил:
 .
.
Елементарною
роботою
 сили
сили
 на переміщенні
на переміщенні
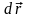 називається скалярна величина
називається скалярна величина
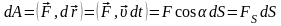 ,
де
,
де
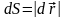 - елементарний шлях, α – кут між векторами
і
,
- елементарний шлях, α – кут між векторами
і
,
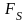 - проекція
вектора
на напрямок вектора
(рис.4).
- проекція
вектора
на напрямок вектора
(рис.4).
 Робота
сили на ділянці траєкторії від точки 1
до точки 2 дорівнює алгебраїчній сумі
елементарних робіт на окремих нескінченно
малих ділянках шляху:
Робота
сили на ділянці траєкторії від точки 1
до точки 2 дорівнює алгебраїчній сумі
елементарних робіт на окремих нескінченно
малих ділянках шляху:
 ,
де
– проекція сили F
на напрямок переміщення. Кінетичною
енергією
механічної системи називається енергія
механічного руху цієї системи:
,
де
– проекція сили F
на напрямок переміщення. Кінетичною
енергією
механічної системи називається енергія
механічного руху цієї системи:
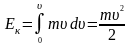 .
.
Зміна кінетичної
енергії тіла дорівнює роботі, яка
виконується над тілом:
 .
.
Потенціальною
енергією
механічної системи називається енергія,
яка залежить від її конфігурації, тобто
від взаємного розміщення всіх матеріальних
точок системи і характеру консервативних
сил, які діють між точками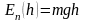 .
Потенціальна енергія деформації
.
Потенціальна енергія деформації
 ,
,
 .
.
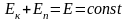 - закон збереження
механічної енергії:
в системі тіл, між якими діють лише
консервативні сили, повна механічна
енергія зберігається, тобто не змінюється
з часом. Відношення кута повороту
радіус-вектора рухомої точки
- закон збереження
механічної енергії:
в системі тіл, між якими діють лише
консервативні сили, повна механічна
енергія зберігається, тобто не змінюється
з часом. Відношення кута повороту
радіус-вектора рухомої точки
 до проміжку часу
,
за який цей поворот відбувається,
називається середньою
кутовою швидкістю точки:
до проміжку часу
,
за який цей поворот відбувається,
називається середньою
кутовою швидкістю точки: .
. Кутовою
швидкістю
називається векторна величина, яка
дорівнює першій похідній кута повороту
тіла за часом:
Кутовою
швидкістю
називається векторна величина, яка
дорівнює першій похідній кута повороту
тіла за часом: .
.
Лінійна
швидкість точки
 .
.
Якщо
за час t
тіло здійснює N
обертів, то час, протягом якого обертове
тіло здійснює один повний оберт
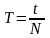 ,
називається періодом
обертання.
З іншого боку, тіло, яке рівномірно
обертається з кутовою швидкістю ,
за час Т повертається на кут .
Тому
,
називається періодом
обертання.
З іншого боку, тіло, яке рівномірно
обертається з кутовою швидкістю ,
за час Т повертається на кут .
Тому
 .
.
Кількість
обертів за одиницю часу називається
частотою
обертання:
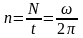 ;
;
 .
.
Середнім
кутовим прискоренням
 називається фізична величина, яка
дорівнює відношенню зміни кутової
швидкості
називається фізична величина, яка
дорівнює відношенню зміни кутової
швидкості
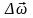 до проміжку часу
до проміжку часу
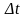 ,
за який ця зміна відбулася:
,
за який ця зміна відбулася:
 .
.
Миттєвим кутовим
прискоренням
 називається границя середнього кутового
прискоренн
називається границя середнього кутового
прискоренн .
.

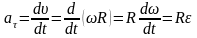 ,
,
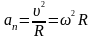 .
.
При
рівнозмінному (=const)
обертанні із виразу
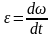 отримуємо:
отримуємо:
 ,
,
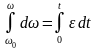 і
і
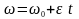 ,
де
,
де
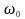 -
кутова швидкість при t=0.
Проінтегрувавши вираз
-
кутова швидкість при t=0.
Проінтегрувавши вираз
 ,
,
отримуємо: ,
,
 .
.
Моментом сили
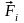 відносно нерухомої точки О
називається векторний добуток
радіус-вектора
відносно нерухомої точки О
називається векторний добуток
радіус-вектора
 ,
який проведений з точки О в точку
прикладання сили, на силу
:
,
який проведений з точки О в точку
прикладання сили, на силу
:
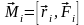 .
.
Вектор
 напрямлений перпендикулярно до площини
векторів
і
(рис. 7).
напрямлений перпендикулярно до площини
векторів
і
(рис. 7).


Модуль моменту
сили
 ,
де
,
де
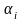 – кут між
і
,
а
– кут між
і
,
а
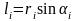 – плече сили – довжина перпендикуляра,
опущеного з точки
– плече сили – довжина перпендикуляра,
опущеного з точки
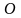 на лінію дії сили
.
на лінію дії сили
.
Моментом
імпульсу
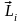 матеріальної точки відносно нерухомої
точки
називається векторний добуток
радіус-вектора
матеріальної точки, який проведений з
точки
,
на імпульс цієї матеріальної точки
матеріальної точки відносно нерухомої
точки
називається векторний добуток
радіус-вектора
матеріальної точки, який проведений з
точки
,
на імпульс цієї матеріальної точки
 (рис.8):
(рис.8):
 .
Модуль вектора моменту імпульсу
.
Модуль вектора моменту імпульсу
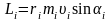 .
.
Векторна
сума моментів імпульсу
всіх матеріальних точок тіла називається
моментом
 імпульсу тіла відносно точки
:
імпульсу тіла відносно точки
:
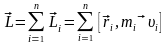 .
Сума добутків мас усіх матеріальних
точок тіла на квадрати їх відстаней до
осі OZ
називається моментом
інерції тіла відносно цієї осі:
.
Сума добутків мас усіх матеріальних
точок тіла на квадрати їх відстаней до
осі OZ
називається моментом
інерції тіла відносно цієї осі:
 .
Отже,
.
Отже,
 .
.
Момент
імпульсу тіла відносно осі
дорівнює добутку моменту інерції тіла
відносно тієї самої осі на кутову
швидкість обертання навколо цієї осі.
М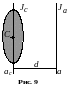 омент
інерції тіла відносно довільної осі
можна розрахувати, використавши теорему
Штейнера:
момент інерції
омент
інерції тіла відносно довільної осі
можна розрахувати, використавши теорему
Штейнера:
момент інерції
 тіла відносно довільної осі
тіла відносно довільної осі
 дорівнює сумі моменту інерції
дорівнює сумі моменту інерції
 тіла відносно паралельної до неї осі
тіла відносно паралельної до неї осі
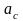 ,
що проходить через центр мас
,
що проходить через центр мас
 тіла, і добутку маси тіла
тіла, і добутку маси тіла
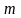 на квадрат відстані
на квадрат відстані
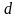 між цими осями (рис. 9):
між цими осями (рис. 9):
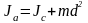 .
Швидкість
зміни моменту імпульсу тіла, що обертається
навколо нерухомої точки, дорівнює
головному моменту відносно цієї точки
всіх зовнішніх сил, які прикладені до
тіла:
.
Швидкість
зміни моменту імпульсу тіла, що обертається
навколо нерухомої точки, дорівнює
головному моменту відносно цієї точки
всіх зовнішніх сил, які прикладені до
тіла:
 .
.
Кінетична
енергія тіла, що рухається довільно,
дорівнює сумі кінетичних енергій всіх
n
матеріальних точок, на які це тіло можна
умовно поділити: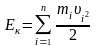 .
.
Якщо
тіло обертається навколо нерухомої осі
OZ
з кутовою швидкістю
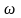 ,
то
,
то
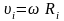 ,
,
де
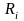 - відстань
від цієї точки до осі обертання. Отже,
- відстань
від цієї точки до осі обертання. Отже,
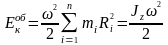 .
.
Якщо
тверде тіло рухається поступально з
швидкістю
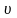 і одночасно обертається з кутовою
швидкістю
навколо осі, що проходить через його
центр інерції, то його кінетична енергія
і одночасно обертається з кутовою
швидкістю
навколо осі, що проходить через його
центр інерції, то його кінетична енергія
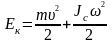 .
.
Елементарна
робота, яка виконується зовнішньою
силою при обертанні тіла,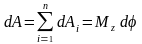 .
.
Закон
збереження моменту імпульсу тіла
відносно осі:
якщо момент зовнішніх сил відносно
нерухомої осі обертання тіла тотожно
дорівнює нулю, то момент імпульсу тіла
відносно цієї осі не змінюється під
час руху:
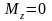 і
і
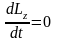 ,
,
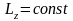 ,
або
,
або
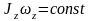 ,
де
,
де
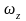 – кутова швидкість тіла,
– кутова швидкість тіла,
 – його момент інерції відносно осі
обертання.
– його момент інерції відносно осі
обертання.
Коливанням називається всякий рух або зміна стану тіла, що характеризується тим чи іншим ступенем повторюваності в часі значень фізичних величин, які визначають цей рух або стан тіла.
Коливання
називаються періодичними,
якщо значення фізичних величин, які
змінюються в процесі коливань, повторюються
через однакові проміжки часу. Найпростішим
типом періодичних коливань є так звані
гармонічні
коливання
– коливання, при яких значення фізичної
величини змінюється з часом за законом
косинуса (синуса). Коливання називаються
вільними
або власними,
якщо вони здійснюються за рахунок
енергії, яка була надана, за відсутності
в наступному зовнішніх періодичних
впливів на коливну систему. Нехай
матеріальна точка здійснює вільні
гармонічні коливання вздовж осі координат
 біля положення рівноваги, яке прийняте
за початок координат. Тоді залежність
координати х від часу
біля положення рівноваги, яке прийняте
за початок координат. Тоді залежність
координати х від часу
 задається рівнянням
задається рівнянням
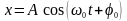 ,
тут x
– зміщення коливної точки;
,
тут x
– зміщення коливної точки;
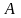 –амплітуда
коливання
–амплітуда
коливання
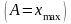 ;
– власна циклічна частота;
;
– власна циклічна частота;
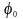 – початкова фаза коливань в момент часу
– початкова фаза коливань в момент часу
 ;
;
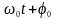 – фаза коливань в момент часу t.
Найменший проміжок часу Т, після
проходження якого повторюються значення
всіх фізичних величин, що характеризують
коливання, називається періодом
коливання.
За час Т здійснюється одне повне коливання
і фаза коливань отримує приріст
– фаза коливань в момент часу t.
Найменший проміжок часу Т, після
проходження якого повторюються значення
всіх фізичних величин, що характеризують
коливання, називається періодом
коливання.
За час Т здійснюється одне повне коливання
і фаза коливань отримує приріст
 ,
тобто
,
тобто
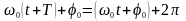 .
Звідси
.
Звідси
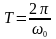 .
Частотою
коливань
називається кількість повних коливань,
що здійснюються за одиницю часу:
.
Частотою
коливань
називається кількість повних коливань,
що здійснюються за одиницю часу:
 ,
де N
– кількість коливань, виконаних за час
t.
,
де N
– кількість коливань, виконаних за час
t.
Частота коливань
– величина, яка обернена до періоду
коливань:
 .
Циклічна частота
.
Циклічна частота
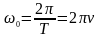 .
.
Коливальний процес характеризується швидкістю і прискоренням коливної точки:

 ,
,

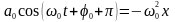 ,
,
де
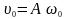 – амплітуда швидкості,
– амплітуда швидкості,
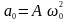 – амплітуда прискорення.
– амплітуда прискорення.

 .
Сила, що діє на коливну матеріальну
точку прямо пропорційна до зміщення і
завжди напрямлена до положення рівноваги.
Тому її називають повертальною силою.
Фаза сили
.
Сила, що діє на коливну матеріальну
точку прямо пропорційна до зміщення і
завжди напрямлена до положення рівноваги.
Тому її називають повертальною силою.
Фаза сили
 збігається з фазою прискорення:
збігається з фазою прискорення:
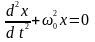 ,
,
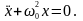
Це диференціальне рівняння вільних гармонічних коливань, збуджених пружними або квазіпружними силами. Загальними розв’язками цього диференціального рівняння є функції:
 або
або
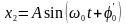 .
.
Кінетична енергія матеріальної точки, що здійснює гармонічні коливання, дорівнює:

 .
.
Потенціальна енергія матеріальної точки, що здійснює гармонічні коливання під дією квазіпружної сили, дорівнює:

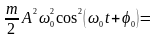
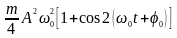 .
.
Повна
механічна енергія коливної точки: .
.
П ружинний
маятник
– це тіло масою
,
яке підвішене на невагомій абсолютно
пружній пружині і здійснює гармонічні
коливання під дією пружної сили
ружинний
маятник
– це тіло масою
,
яке підвішене на невагомій абсолютно
пружній пружині і здійснює гармонічні
коливання під дією пружної сили
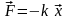 ,
де
,
де
 – коефіцієнт пружності, який у випадку
пружини називається жорсткістю (рис. 10).
На тіло діє і сила тяжіння
– коефіцієнт пружності, який у випадку
пружини називається жорсткістю (рис. 10).
На тіло діє і сила тяжіння
 .
.
Запишемо основне рівняння динаміки для цього випадку:
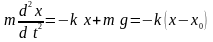
 ,
де
,
де
 -
-
статична деформація пружини під дією сила тяжіння mg.
Позначимо
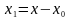 і, враховуючи, що
і, враховуючи, що
 ,
бо
,
бо
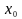 не залежить від часу, знайдемо рівняння
руху тіла:
не залежить від часу, знайдемо рівняння
руху тіла:
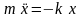 ,
, ,де
,де
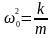 .
.
Отже, пружинний маятник здійснює вільні гармонічні коливання за законом
з
власною циклічною частотою
 і
періодом
і
періодом
 .
.
Період коливань Т не залежить від амплітуди А. Ця формула справедлива для пружних коливань в межах, в яких виконується закон Гука, та коли маса пружини мала порівняно з масою тіла.
Потенціальна
енергія пружинного маятника дорівнює:
 ,а
кінетична:
,а
кінетична: .
.
М атематичним
маятником
називається матеріальна точка, яка
підвішена на невагомій і нерозтяжній
нитці. На практиці математичним маятником
можна вважати важке тіло, яке підвішене
на легенькій нитці, довжина якої набагато
більша, ніж розміри тіла (рис. 11). Якщо
відхилити маятник з положення рівноваги
так, щоб нитка утворювала кут
атематичним
маятником
називається матеріальна точка, яка
підвішена на невагомій і нерозтяжній
нитці. На практиці математичним маятником
можна вважати важке тіло, яке підвішене
на легенькій нитці, довжина якої набагато
більша, ніж розміри тіла (рис. 11). Якщо
відхилити маятник з положення рівноваги
так, щоб нитка утворювала кут
 з вертикаллю, то він почне коливатися
у вертикальній площині під дією сили
тяжіння
.
з вертикаллю, то він почне коливатися
у вертикальній площині під дією сили
тяжіння
.
Сила,
що повертає математичний маятник у
положення рівноваги, є складовою
його сили тяжіння
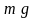 :
: .
Складова
.
Складова
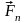 зрівноважується силою натягу нитки
зрівноважується силою натягу нитки
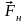 .
Силу що повертає маятник до положення
рівноваги, можна вважати квазіпружною
силою:
.
Силу що повертає маятник до положення
рівноваги, можна вважати квазіпружною
силою: .
Отже, малі коливання математичного
маятника – гармонічні. Період цих
коливань дорівнює:
.
Отже, малі коливання математичного
маятника – гармонічні. Період цих
коливань дорівнює:
 .
.
Період малих коливань математичного маятника не залежить від амплітуди коливань.
Фізичний
маятник –
абсолютно тверде тіло, що здійснює
коливання під дією сили тяжіння навколо
горизонтальної осі О, яка не проходить
через його центр мас С (рис. 12). При
малих коливаннях фізичний маятник
здійснює гармонічні коливання з частотою
і періодом
 ,
де
,
де
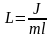 - зведена довжина фізичного маятника.
- зведена довжина фізичного маятника.
Нехай
точка бере участь у двох гармонічних
коливаннях однакової частоти, які
напрямлені вздовж однієї прямої: ,
,
 .
.
Ці
коливання зручно додати, користуючись
методом обертального вектора амплітуди.
Для цього відкладемо з точки О під кутом
 вектор амплітуди
вектор амплітуди
 ,
а під кутом
,
а під кутом
 - вектор амплітуди
- вектор амплітуди
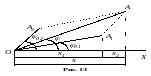
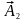 (рис. 13). Оскільки вектори
і
обертаються з однаковою кутовою
швидкістю, то різниця фаз
(рис. 13). Оскільки вектори
і
обертаються з однаковою кутовою
швидкістю, то різниця фаз
 між ними постійна. Оскільки сума проекцій
двох векторів на одну вісь дорівнює
проекції на ту саму вісь вектора, який
є їх сумою, то результуюче коливання
можна подати вектором амплітуди
між ними постійна. Оскільки сума проекцій
двох векторів на одну вісь дорівнює
проекції на ту саму вісь вектора, який
є їх сумою, то результуюче коливання
можна подати вектором амплітуди
 ,
що дорівнює сумі векторів
,
що дорівнює сумі векторів
і
:
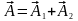
і
який обертається навколо точки
з тією самою кутовою швидкістю
,
що й вектори
і
.
Результуюче коливання описуються
рівнянням
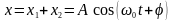 ,
,
де – амплітуда результуючого коливання, а – його початкова фаза.
Застосовуючи
теорему косинусів до одного з трикутників,
на які паралелограм розбивається
діагоналлю, з рис. 13 видно, що
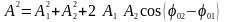 ,
, .
.
Амплітуда
A
результуючого коливання залежить
від різниці початкових фаз
коливань, що додаються. Можливі значення
A
лежать в межах
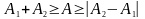 .
.
Отже,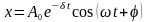 ,
де
,
де
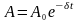 - амплітуда загасаючих коливань, а
- амплітуда загасаючих коливань, а
 - початкова амплітуда. Амплітуда згасаючих
коливань зменшується з плином часу і
тим скоріше, чим більший коефіцієнт
опору і чим менша маса
коливного тіла. Величина
- початкова амплітуда. Амплітуда згасаючих
коливань зменшується з плином часу і
тим скоріше, чим більший коефіцієнт
опору і чим менша маса
коливного тіла. Величина
 називається власною циклічною частотою
коливань дисипативної системи. Графік
залежності x від часу наведений на
рис. 36.
називається власною циклічною частотою
коливань дисипативної системи. Графік
залежності x від часу наведений на
рис. 36.

Згасаючі
коливання – неперіодичні коливання,
бо в них ніколи не повторюються, наприклад,
максимальні значення зміщення,
швидкості і прискорення. Однак при
згасаючих коливаннях величина x
перетворюється в нуль, змінюючись в
один і той самий бік, а також досягає
максимальних і мінімальних значень
через однакові проміжки часу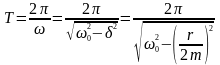 .
Величину T
тому називають періодом згасаючих
коливань. Якщо
.
Величину T
тому називають періодом згасаючих
коливань. Якщо
 і
і
 – амплітуди двох послідовних коливань,
що йдуть одне за одним через проміжок
часу T,
то відношення
– амплітуди двох послідовних коливань,
що йдуть одне за одним через проміжок
часу T,
то відношення
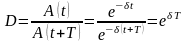 називається
декрементом
згасання,
а його натуральний логарифм
називається
декрементом
згасання,
а його натуральний логарифм
 –
логарифмічний
декремент згасання.
–
логарифмічний
декремент згасання.
Процес
поширення коливань в суцільному
середовищі, яке неперервно розподілене
в просторі і має пружні властивості,
називається механічним
хвильовим процесом, або механічною
хвилею.
При поширенні хвилі частинки середовища
не рухаються разом з хвилею, а коливаються
біля своїх положень рівноваги. Основна
властивість всіх хвиль є перенесення
енергії без перенесення речовини.
Пружними (або механічними) хвилями
називаються механічні збурення, що
поширюються у пружному середовищі.
Пружні хвилі бувають поперечні і
поздовжні. Відстань між найближчими
частинками, що коливаються однаковим
чином, називається довжиною
хвилі
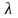 .
Довжина хвилі дорівнює тій відстані,
на яку поширюється певна фаза коливань
за період:
.
Довжина хвилі дорівнює тій відстані,
на яку поширюється певна фаза коливань
за період:
 і
і
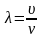 .
Поверхня, до якої доходять коливання в
деякий момент часу, називається фронтом
хвилі.
Поверхня, в якій всі частинки коливаються
з однаковими фазами, називається
хвильовою.
.
Поверхня, до якої доходять коливання в
деякий момент часу, називається фронтом
хвилі.
Поверхня, в якій всі частинки коливаються
з однаковими фазами, називається
хвильовою.
Хвиля називається плоскою, якщо її хвильові поверхні мають вигляд площин, які паралельні до площини, що проходить через джерело хвиль. Хвиля називається сферичною, якщо її хвильові поверхні мають вигляд концентричних сфер. Напрямки, в яких поширюються коливання, називаються променями.
Рівняння біжучої плоскої хвилі, що поширюється вздовж осі , має такий вигляд:
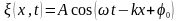 ,
де А
– амплітуда коливань, яка називається
амплітудою хвилі;
,
де А
– амплітуда коливань, яка називається
амплітудою хвилі;
 – циклічна частота хвилі;
– початкова фаза коливань в площині
– циклічна частота хвилі;
– початкова фаза коливань в площині
 .
.
Приклад 1
Орел,
побачивши на землі мишу, починає
знижуватись з швидкістю 10 м/c, рухаючись
під кутом ![]() =300 до поверхні
землі. Знайдіть швидкість, з якою
рухається тінь орла по землі. Поверхню
землі вважайте горизонтальною.
=300 до поверхні
землі. Знайдіть швидкість, з якою
рухається тінь орла по землі. Поверхню
землі вважайте горизонтальною.
Розв’язання:
|
Пов’яжемо систему
відліку з землею. Вісь координат ОХ спрямуємо
в одну сторону з напрямом руху орла.
Зробимо схематичний малюнок (рис 4.1),
на якому покажемо вектор швидкості
орла
рис 1.1 |
Тоді проекція вектора швидкості на вісь ОХ ( ), що знаходиться у горизонтальній площині – це буде величина вектора швидкості, з якою рухається тінь орла по землі.
Величину
знайдемо
з прямокутного трикутника ![]() ПП1К з
означення косинуса:
ПП1К з
означення косинуса:
![]()
![]()
Відповідь: ʋ = 8,7м/с.
Приклад 2
Швидкість течії річки 3км/год, а швидкість руху човна відносно води 6км/год. Визначити, під яким кутом відносно берегу повинен пливти човен, щоб перпендикулярно перепливти річку.
Д ано:
ано:
ʋ 1=3км/год
cos
α= ʋ1/
ʋ2 ʋ2
1=3км/год
cos
α= ʋ1/
ʋ2 ʋ2
ʋ2=6км/год
α=arccos(ʋ1/ ʋ2)
α - ? α=60° α ʋ1
Рис 1.2.
Відповідь: 60°
Приклад 3
На рис 1.3. показані графіки зміни координат трьох тіл, що рухаються прямолінійно. Записати закони руху кожного тіла і визначити, яке тіло має більшу швидкість. Побудувати графік швидкості цього тіла.

Рис 1.3.
Розв’язання:
Початкові координати тіл:х01 = 0м, х02 = 0м, х03 = -4м.
Через певний проміжок часу, наприклад 4с, координати тіл будуть: х1 = 8м, х2 = 4м, х3 = 0м.
Т оді
швидкості тіл знаходимо за формулою
оді
швидкості тіл знаходимо за формулою


З
відки
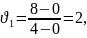

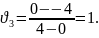 2
2
Н
айбільшу
швидкість має перше тіло
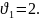
Тоді рівняння руху х = х0 + ʋ*t і остаточно маємо 1
х 1 = 2*t, x2 = t, x3 = -4 + t.
t
Відповідь: х1 = 2*t, x2 = t, x3 = -4 + t. Найбільша швидкість
Приклад 4
Рівняння руху матеріальної точки вздовж осі має вид х = А + Вt + Ct3, де А = 2 м, В = 1 м/с, С = – 0,5 м/с3. Знайти координату х, швидкість υ та прискорення а в момент часу t = 2 с.
Розв’язок.
Координату х знайдемо, підставивши в рівняння руху числові значення коефіцієнтів А, В і С та часу t:
х
= (2 + 1
2 – 0,5
23)
м = 0.Миттєва швидкість є перша похідна
від координати за часом: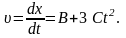
В
момент часу t
= 2 с υ
= (1 – 3
0,5
22)
м/с = – 5 м/с.Прискорення точки знайдемо,
взявши першу похідну від швидкості за
часом:
 В
момент часу t
= 2 с а = 6 (– 0,5)
2 м/с2
= – 6 м/с2.
В
момент часу t
= 2 с а = 6 (– 0,5)
2 м/с2
= – 6 м/с2.
Приклад 5
Тіло обертається навколо нерухомої осі за законом = А + Вt + Сt2, де А = 10 рад, В = 20 рад/с, С = - 2 рад/с2. Знайти повне прискорення точки, яка знаходиться на відстані r = 0,1 м від осі обертання, на момент часу t = 4 с.
Розв’язок.
Повне
прискорення
точки, яка рухається по кривій лінії,
може бути знайдено як геометрична сума
тангенційного прискорення
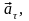 яке
направлене по дотичній до траєкторії,
і нормального прискорення
яке
направлене по дотичній до траєкторії,
і нормального прискорення
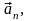 направленого до центру кривизни
траєкторії (рис. 1).
направленого до центру кривизни
траєкторії (рис. 1).
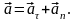 Так
як вектори
і
взаємно перпендикулярні, то абсолютне
значення прискорення
Так
як вектори
і
взаємно перпендикулярні, то абсолютне
значення прискорення
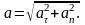 (1)
(1)
Тангенційне і нормальне прискорення точки тіла яке обертається виражаються формулами:
 Рисунок
1.
Рисунок
1.
а = r, an = 2 r, де – кутова швидкість тіла; - його кутове прискорення.
Підставляючи
вираз для а
і аn
в формулу (1), знаходимо
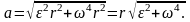 (2)
(2)
Кутову
швидкість
знайдемо, взявши похідну від кута
повороту за часом:

На момент часу t = 4 с кутова швидкість = [20 + 2 (-2) 4] рад/с = 4 рад/с.
Кутове
прискорення знайдемо, взявши похідну
від кутової швидкості за часом: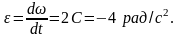
Цей
вираз не містить параметру часу; отже,
кутове прискорення заданого руху
постійне. Підставляючи знайдені значення
і
і задане значення r
в формулу (2), отримаємо

Приклад 6
Тіло кинуто під кутом 30° до горизонту з початковою швидкістю 50м/с.Визначити висоту підйому, дальність польоту та час польоту.
Розв’язок.
Час
польоту t
=
 = 2*50м/с*
= 2*50м/с* /9,81м/с2
/9,81м/с2
 5,1с.
5,1с.
Дальність
польоту l
=
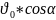 *t
=
*t
=
 *
=
*
=
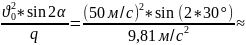 221м.
221м.
Висота
підйому h
=
 63,7м
63,7м
Приклад 7
Камінь вільно падає в шахту з водою. Через 6с чутно сплеск води. Визначте глибину шахти, якщо швидкість звуку 330м/с.
Розв’язок.
Рух
каменя є рівноприскореним, тому висота
шахти h
=
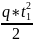 .
Звук поширюється рівномірно, тому h=
ʋ*t2.
.
Звук поширюється рівномірно, тому h=
ʋ*t2.
Загальний
час t1+t2
= 6c,
звідки t2
= 6 - t1
і
 6
- t1)*
ʋ. Розв'язавши рівняння отримаємо t1
5,54c.
6
- t1)*
ʋ. Розв'язавши рівняння отримаємо t1
5,54c.
Тоді глибина шахти h 150,7м.
Приклад 8
Тіло кидають вертикально вверх зі швидкістю 100м/с. Визначити максимальну висоту підйому та час підйому.
Розв’язок.
Рух
тіла є рівносповільненим, тому h
= ʋ0*t
-
 .
.
Кінцева
швидкість дорівнює нулю, а тому ʋ=
ʋ0-g*t
і
час підйому t
=
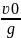 =
=
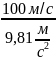 10,2с.
10,2с.
Максимальна
висота підйому
h
= g*t
*t
-
 =
=
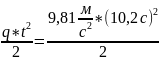 509,7м.
509,7м.
Приклад 9
Розв’язок.
Ящик масою m1 = 20 кг зісковзується по ідеально гладкому лотку довжиною l = 2 м на нерухомий візок з піском і застряє в ньому. Візок з піском масою m2 = 80 кг може вільно (без тертя) переміщуватись по рейках в горизонтальному напрямку. Визначити швидкість и візка з ящиком, якщо лоток нахилений під кутом = 300 до рейок.
Розв’язок.
Візок
і ящик можна розглядати як систему двох
тіл, які непружньо взаємодіють. Але ця
система не замкнена, так як сума зовнішніх
сил, яка діє на систему: двох сил тяжіння
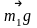 і
і
 та
сили реакції
та
сили реакції
 (рис. 2) не дорівнює нулю. Тому застосувати
закон збереження імпульсу до системи
ящик-візок не можна. Але так як проекція
суми вказаних сил на напрямок осі х, яка
співпадає з напрямком рейок, дорівнює
нулю, складову імпульсу системи в цьому
напрямку можна вважати постійною, тобто
(рис. 2) не дорівнює нулю. Тому застосувати
закон збереження імпульсу до системи
ящик-візок не можна. Але так як проекція
суми вказаних сил на напрямок осі х, яка
співпадає з напрямком рейок, дорівнює
нулю, складову імпульсу системи в цьому
напрямку можна вважати постійною, тобто

Рисунок 2.
р1х + р2х = р/1х + р/2х, (1)
де р1х і р2х – проекції імпульсу ящика і візка з піском в момент падіння ящика на візок;
р/1х і р/2х – ті самі величини після падіння ящика.
Виразимо в рівнянні
(1) імпульси тіл через їх маси і швидкості,
враховуючи, що р2х
= 0 (візок до взаємодії з ящиком покоївся),
а також той факт, що після взаємодії
обидва тіла системи рухаються з однією
швидкістю и: m1υix
= (m1
+ m2)
 ,
або m1υi
cos
= (m1
+ m2)
,де
υi
– швидкість ящика перед падінням на
візок;
,
або m1υi
cos
= (m1
+ m2)
,де
υi
– швидкість ящика перед падінням на
візок;
υix
= υi
cos
– проекція цієї швидкості на вісь х.
Звідси виразимо шукану швидкість:
 (2) Швидкість
υ1
визначимо за законом збереження енергії:
(2) Швидкість
υ1
визначимо за законом збереження енергії:
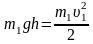 ,
де h
= l
sin
.
Після скорочення на m1
знайдемо
,
де h
= l
sin
.
Після скорочення на m1
знайдемо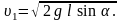 Підставивши
визначений вираз υ1
в формулу
(2), одержимо:
Підставивши
визначений вираз υ1
в формулу
(2), одержимо:
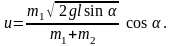 Підставимо
сюди числові значення величин і проведемо
розрахунки:
Підставимо
сюди числові значення величин і проведемо
розрахунки: