16. Оформите работу. Сделайте выводы.

ЛИТЕРАТУРА

1. Уэндландт У. Термические методы анализа. М.: Мир, 1978. 526 С.

2. Дифференциально-термический анализ металлов и сплавов: метод. указания к лаб. работе N 713 по курсу "Физика" для студентов, обучающихся по специальности 010701 "Физика" / Урал. гос. техн. ун-и - УПИ ; [сост. В. М. Замятин, О. П. Московских ; науч. ред. Ф. А. Сидоренко]. - Екатеринбург: УГТУ-УПИ, 2006. - 10 с.: URI: http://hdl.handle.net/123456789/2115

3. Я.Шестак. Теория термического анализа. М. Мир, 1987. 338 С.

ПРИЛОЖЕНИЕ

Программирование криотермостата на достижение необходимой температуры

Включите выключатель (красного цвета) на управляющей головке криотермостата ТЖ-ТС-01. На панели должно загореться сообщение «Start» после чего прибор перейдет в режим достижения введенной температуры.

Нажмите кнопку «» (правая нижняя в ряду управляющих кнопок прибора) и, пользуясь стрелками «» и «», требуемую Снова нажмите на кнопку «». Эта процедура даст прибору задание на установление указанной температуры в приборе. Если указанная температура уже выставлена на индикаторе, сразу нажмите кнопку «». (Здесь и далее: в случае, если заданного Вами изменения температуры не происходит, попробуйте выключить и включить прибор)

ПРИЛОЖЕНИЕ 1

Вывод осмотического уравнения Вант-Гоффа

Уравнение Вант-Гоффа для идеальных растворов можно получить на основании термодинамических соображений. Растворитель будет проникать в раствор через полупроницаемую перегородку до тех пор, пока в системе не установится равновесие. При равновесии химические потенциалы растворителя в растворе (μ₁) и в чистом растворителе (μ₁) будут одинаковы

μ₁ = μ₁. (П.1)

При постоянных температуре (T) и давлении (P)

μ₁ = const, (П.2)

а

μ₁ = f(P₁, x₁) (П.3),

где Р₁ = Ρ + ; Ρ — давление, при котором находится раствор (а, изначально – находился и растворитель),  — осмотическое давление. Под x₁ будем понимать молярную долю растворителя, под x₂ – молярную долю примеси, которая задерживается перегородкой.

Так как

μ₁ = f(P₁, x₁),

то (П.4)

. (П.5)

В условиях равновесия при учете (П.1) и (П.2)

(П.6)

Следовательно,

(П.7)

Так как

, (П.8)

то

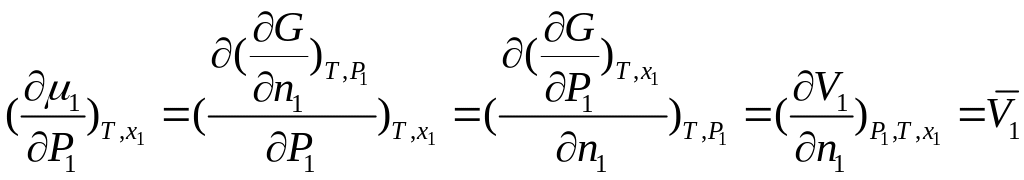(П.9)

где — парциальный молярный объем растворителя. При дифференцировании уравнения (П.10) по х₁ получаем (П.11):

(П.10)

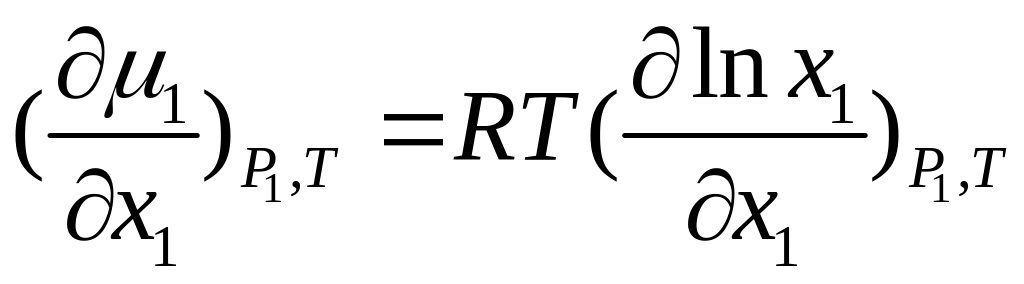. (П.11)

Выражения (П.9) и (П.11) подставляем в (П.7) и получаем

(П.12)

При интегрировании (П.12) от P₁ = P до P₁ = P+ и от x₁=1 до x₁ в предположении, что не зависит от x₁ и P₁, получаем:

;

. (П.13)

Для идеального раствора — молярный объем чистого растворителя. Поэтому в идеальном растворе

. (П.14)

В разбавленных растворах молярная доля примеси x₂ близка нулю. Это позволяет воспользоваться разложением

(П.15)

Далее учтем, что n₂<<n₁, поэтому

(П.16)

Подставляем (П.15) и (П.16) в (П.14), и, ограничиваясь в (П.15) первым членом, получаем уравнение Вант-Гоффа:

, (П.17)

где С₂ – молярная концентрация примеси в растворе.

1 Здесь и далее при использовании терминов твердое тело (фаза) и твердые растворы будем подразумевать их кристаллическую организацию.

2 Напомним, что под сложными понимаются вещества, образованные атомами различных элементов.

3 В некоторых твердых растворах имеются аналогичные, однако это тема для отдельного разговора.

41