§6. Отношение порядка и упорядоченные множества

Рассмотрим отношения:

1. отношение меньше или равно на множестве N натуральных чисел;

2. отношение нестрогого включения 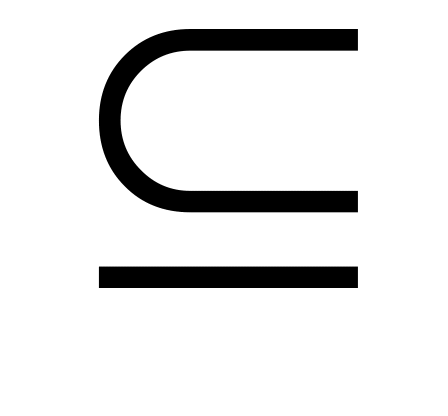на множестве подмножеств множества М;

3. отношение делимости 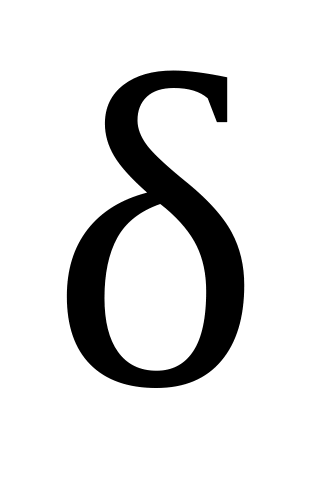на множестве N, т.е. 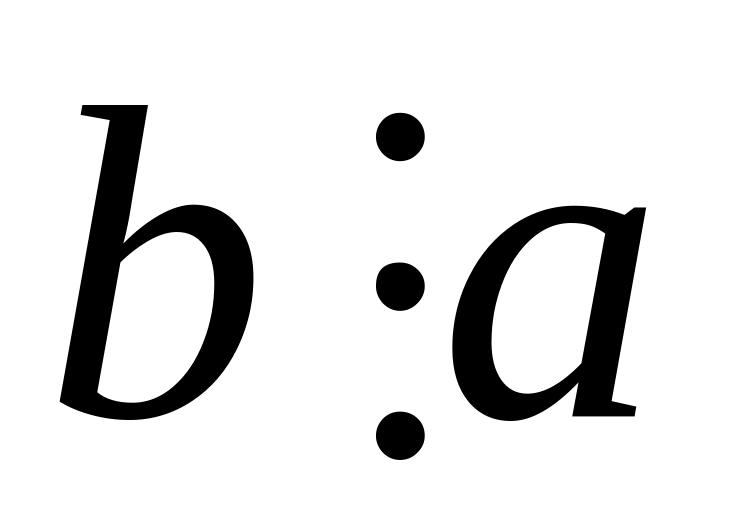(b делится на a);

4. отношение строго меньше на множестве R действительных чисел;

5. отношение строго включения 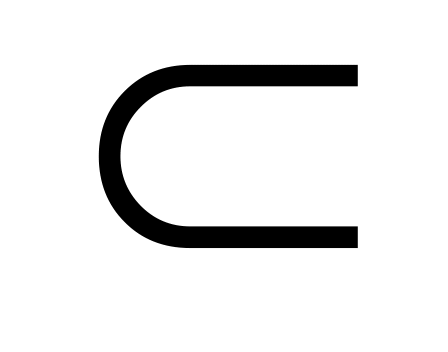на множестве подмножеств множества М.

Нетрудно проверить, что каждое из этих отношений антисимметрично и транзитивно.

Кроме того, интуитивно ясно, что каждое из этих отношений определяет некоторый «порядок» на соответствующем множестве.

Определение 1. Если бинарное отношение на множестве М антисимметрично и транзитивно, то оно называется отношением порядка, а само множество М – упорядоченным.

Определение 2. Если порядок на множестве М рефлексивен, то он называется нестрогим порядком, а само множество М – нестрого упорядоченным.

Определение 3. Если порядок на множестве М антирефлексивен, то он называется строгим порядком, а само множество М – строго упорядоченным.

Отношения нестрогого порядка будем обозначать символом меньше или равно , а строгого порядка – символом строго меньше .

Для каждого отношения нестрогого порядка существует родственное ему отношение строгого порядка и наоборот:

; .

С другой стороны, каждому из порядков , можно поставить в соответствие двойственные им порядки больше или равно , строго больше по следующему правилу:

; .

Примеры 2, 3 и 5 показывают, что в упорядоченном множестве могут встречаться и не сравнимые пары элементов: например, 3 не делится на 4 и 4 не делится на 3; если , то подмножество не включается в подмножество и не включается в .

Т е о р е м а . Антирефлексивное и транзитивное отношение является антисимметричным.

□ Предположим, что антирефлексивное и транзитивное отношение не является антисимметричным. Тогда справедливо следующее высказывание:

.

Отсюда в силу транзитивности отношения получим , а это противоречит антирефлексивности отношения .

Доказанная теорема позволяет дать другое, эквивалентное определению 3, определение строгого порядка.

Определение . Антирефлексивное и транзитивное отношение называется строгим порядком.

Определение 4. Если в упорядоченном множестве М любые два различных элемента сравнимы между собой, то множество М называется линейно упорядоченным, а само отношение порядка – линейным порядком; если в этом множестве есть несравнимые элементы, то множество называют частично упорядоченным, а само отношение – отношением частичного порядка.

Другими словами, если в упорядоченном множестве порядок связен, то оно называется линейно упорядоченным; в противном случае множество называется частично упорядоченным.

В примере 1 и 4 порядок является линейным, причем в примере 1 нестрогим, а в примере 4 – строгим. В примерах 2 и 3 отношения являются отношениями нестрогого частичного порядка, а в примере 5 – отношением строгого частичного порядка.

Определение 5. Пусть – произвольный элемент упорядоченного множества М. Элемент называется соседним предшествующим для , если строго меньше и в нет элемента строго больше, чем и строго меньше, чем . Элемент называется соседним последующим для , если строго больше и в нет элемента строго большего и строго меньшего, чем .

При графическом изображении отношений порядка обычно петли не рисуют; стрелки также опускают, а точки, изображающие элементы и , соединяют отрезком тогда и только тогда, когда является соседним предшествующим для и при этом изображают ниже (иногда, в случае линейного порядка, левее) . Полученное изображение называют диаграммой упорядоченного множества. Понятно, что диаграмма линейно упорядоченного множества представляет собой прямую линию, что объясняет происхождение термина. Ниже на рис. 1 изображены диаграммы следующих упорядоченных множеств: а) ; б) ; в) ; г) ; д) .

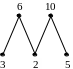
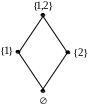
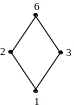
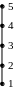
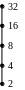
а) б) в) г) д)

Рис. 1.

Определение 6. Пусть – упорядоченное множество и – произвольное подмножество множества . Наименьшим элементом подмножества называется такой его элемент , что для любого имеет место ; наибольшим элементом подмножества называется такой его элемент , что для любого имеет место . Минимальным элементом подмножества называется такой его элемент, для которого нет соседнего предшествующего. Максимальным элементом подмножества называется такой его элемент, для которого нет соседнего последующего.

Известно, что в линейно упорядоченном множестве любое подмножество имеет наименьший элемент, в частности 1 – наименьший элемент в N. Понятно, что наименьший элемент подмножества является минимальным. Для линейно упорядоченных множеств верно и обратное утверждение, но для частично упорядоченных, вообще говоря, это не так. Аналогично обстоит дело с наибольшими и максимальными элементами. Например, в диаграмме в) множество имеет три минимальных элемента 2, 3 и 5 и два максимальных элемента 6 и 10, но не имеет ни наименьшего, ни наибольшего.

Определение 7. Упорядоченное множество называется вполне упорядоченным, если любое его подмножество имеет наименьший элемент.

Так как любое двухэлементное подмножество вполне упорядоченного множества имеет наименьший элемент, то любые его два различных элемента сравнимы и поэтому любое вполне упорядоченное множество является линейно упорядоченным.

Определение 8. Упорядоченное множество М называется дискретным, если каждый его элемент, не являющийся минимальным в М, обладает соседним предшествующим, а каждый элемент, не являющийся максимальным в М, имеет соседний последующий. Упорядоченное множество М называется плотным, если в истинно высказывание:

.

Ясно, что любое конечное упорядоченное множество является дискретным. Упорядоченные множества , , , из примеров 1, 2, 3 и 5 дискретны, а упорядоченное множество из примера 4 является плотным.

Определение 9. Нижней гранью произвольное подмножество множества называется любой элемент из , который меньше или равен любого элемента из ; наибольший элемент в множестве всех нижних граней называется точной нижней гранью и обозначается . Верхней гранью произвольное подмножество множества называется любой элемент из , который больше или равен любого элемента из ; наименьший элемент в множестве всех верхних граней называется точной верхней гранью и обозначается .

Определение 10. Подмножество множества называется ограниченным снизу, если оно имеет нижнюю грань, и ограниченным сверху, если имеет верхнюю грань в . Подмножество множества называется ограниченным, если оно ограничено и снизу и сверху.