Свойство (5) по закону контрапозиции равносильно следующему свойству:

. ( )

Определение 4 можно модифицировать для отображений.

Определение 5. Отображение называется инъективным, если для любого элемента из существует не более одного прообраза в .

Символически свойство инъективности отображения выражается одним из следующих эквивалентных условий:

, (6)

; ( )

т.е. различные элементы множества имеют различные образы, или, что равносильно, если образы двух элементов равны, то и сами элементы равны, так как согласно определению 5 элемент из не может иметь два различных прообраза в .

Граф инъективного отображения (инъективной функции) характеризуется тем, что к любому элементу множества идет не более одной стрелки. Инъективные отображения называют также вложениями.

В примере 1 элемент 9 имеет два прообраза (см. рис. 1) и, следовательно, отображение не инъективно. В примере 2 нечетные числа не имеют прообразов, а четные – по одному прообразу. Значит, отображение такое, что инъективно. Аналитически это доказывается проверкой справедливости свойства ( ) для :

.

Упражнение 1. Выяснить, является ли инъективной функция из примера 3.

Определение 6. Функция называется сюръективной, если каждый элемент из является значением по крайней мере одного элемента из , т.е. множество значений функции совпадает с .

Это определение для отображений модифицируется следующим образом:

Определение 7. Отображение называется сюръективным, если каждый элемент из имеет не менее одного прообраза, т.е. .

Граф сюръективного отображения или сюръективной функции характеризуется тем, что к каждому элементу из идет не менее одной стрелки. В примерах 1 и 2 отображения не сюръективны. Если же в примере 1 взять , а в примере 2 вместо N взять множество 2N всех четных чисел, то соответствующие отображения станут сюръективными.

Для доказательства сюръективности отображения или функции достаточно убедиться в справедливости следующего высказывания:

. (7)

При аналитическом задании сюрьективность будет обеспечена если из формулы при любом из можно выразить x через y и показать, что элемент x принадлежит множеству B. Проиллюстрируем сказанное для отображения такого, что . Рассмотрим уравнение во множестве N натуральных чисел. Выражая x через y, получим . Понятно, что при четном число будет натуральным, а при нечетном число будет дробным. Следовательно, нечетные числа не имеют прообразов и поэтому отображение не сюръективно.

Упражнение 2. Выяснить, является ли сюръективной функция из примера 3.

Сюръективное отображение называют также «отображением на » (сюръективность подчеркивается тем, что вместо предлога «в» используется предлог «на»). Иногда сюръективные отображения называются наложениями.

Определение 8. Если отображение и сюръективно, и инъективно, то оно называется биективным или биекцией.

Таким образом, отображение биективно тогда и только тогда, когда каждый элемент множества имеет единственный прообраз в А. В графе биективного отображения из каждого элемента А выходит единственная стрелка, и в каждый элемент В приходит единственная стрелка.

Определение 9. Если существует биективное отображение , то говорят, что между А и В можно установить взаимно однозначное соответствие, а сами множества А и В называют равномощными.

В случае конечности равномощные множества имеют одинаковое количество элементов.

Укажем еще ряд примеров к приведенным выше определениям.

Пример 4. Пусть , и бинарные отношения заданы следующими графами:

а) б) в)

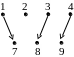
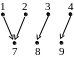
Рис. 2.

Бинарное отношение, определяемое графом а), не является функцией (и тем более отображением), так как из элемента 4 выходит две стрелки. Граф б) определяет инъективную и сюръективную функцию, которая не является отображением, так как из элемента 2 не выходит стрелка. Наконец, граф в) определяет сюръективное, но не инъективное отображение (в элемент 7 приходит две стрелки).

Пример 5. Отображение , где биективно, так как для любого существует единственный прообраз .

Упражнение 3. Доказать, что

а) отображение , не инъективно и не сюръективно;

б) отображение , (здесь черта означает взятие сопряженного) биективно;

в) отображение , не инъективно, но сюръективно.

В заключение подчеркнем, что в определениях функции и отображения множества и произвольны. В частности, если , то функция каждой паре ставит в соответствие единственный элемент . Это уже функция двух переменных и . Ее обозначают через .

Аналогично, если , то получается функция от переменных.

Пример 6. Пусть , . Тогда формула определяет функцию от двух переменных, при которой .

2. Обратные функции и отображения. Как уже отмечалось в предыдущем разделе, что если – бинарное отношение, то и дополнение также является бинарным отношением. Введем еще одну операцию – взятия обратного отношения.

Определение 10. Пусть – некоторое бинарное отношение. Бинарное отношение , определенное условием

(8)

называется обратным по отношению к .

Условие (1) показывает: чтобы получить , достаточно в каждой паре поменять местами компоненты, а в графе отношения направления стрелок поменять на противоположные.

Пример 7. Пусть , и . Тогда . Графически отношения и изображены на рис. 3 ( слева, а справа).

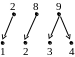
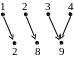
Рис. 3.

Из этого примера видно, что отношение является отображением в , а обратное отношение не является отображением в .

Определение 11. Если – функция, а обратное отношение тоже является функцией, то оно называется обратной функцией по отношению к и обозначается через ; функция в этом случае называется обратимой.

Аналогичная терминология принимается и для отображений.

Т е о р е м а 1. Для функции существует обратная функция тогда и только тогда, когда – инъективная функция. При этом обратная функция также инъективна.

□ Необходимость. Пусть – обратимая функция и предположим, что – не инъективна. Тогда в графе функции существует элемент , к которому приходит более одной стрелка. Значит, в графе обратного отношения из элемента выходит более одной стрелки. Следовательно, не является функцией, что противоречит обратимости функции .

Достаточность. Пусть – инъективная функция. Ее граф характеризуется тем, что к каждому элементу приходит не более одной стрелки. Если изменить направления стрелок на противоположные, то получится граф обратного отношения , в котором из каждого элемента будет выходить не более одной стрелки. Это означает, что – функция из в . Следовательно, функция обратима.

Наконец, очевидно, что в графе функции к каждому элементу приходит не более одной стрелки, т.е. – инъективная функция.

Т е о р е м а 2. Отображение обратимо тогда и только тогда, когда биективно. При этом обратное отображение тоже биективно.

□ В самом деле, если отображение обратимо, то по теореме 1 – инъективное отображение. Если предположить, что отображение не сюръективно, то существует элемент , к которому в графе не идет ни одной стрелки. Следовательно, в графе обратного отношения из элемента у не выходит стрелка, т.е. не является отображением, что противоречит обратимости отображения . Таким образом, – биекция.

Обратно, если – биективное отображение, то его граф характеризуется тем, что из каждого элемента выходит только одна стрелка и к каждому элементу приходит в точности одна стрелка. Если изменить направления стрелок на противоположные, то получится граф обратного отношения , который обладает аналогичным свойством. Значит, – биективное отображение в и, следовательно, отображение обратимо.

Пример 8. а) Отображение , где , не имеет обратного отображения, так как не сюръективно.

б) , где , – множество всех четных натуральных чисел, имеет обратное отображение , причем .

3. Умножение функций и отображений. Введем сначала понятие произведения двух бинарных отношений.

Определение 12. Пусть и – два бинарных отношения. Тогда произведением (композицией) отношений и называется бинарное отношение , определенное следующим условием:

. (9)

На языке графов произведение определяется так: элемент соединяем стрелкой с элементом тогда и только тогда, когда существует такой элемент , что к приходит стрелка из и из выходит стрелка к .

Пример 9. Пусть , , . Ниже следующие графы задают бинарные отношений , и их произведение (см. рис 4).

Замечание 1. В определении 2 взяты не произвольные бинарные отношения, а те у которых область значений первого и область определения второго содержаться в одном и том же множестве . Однако и в этом случае элемента со свойством (9) может не оказаться ни для каких пар . В таком случае произведение есть пустое бинарное отношение . Понятно также, что если , то , если , то . Вообще по аналогии с определением 2 можно определить произведение любых бинарных отношений и . При этом, если , то всегда .

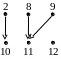
Рис. 4.

Замечание 2. Если – множество бинарных отношений, определенных на множестве , то произведение любых двух элементов является элементом из и можно доказать, что операция умножения бинарных отношений из ассоциативна, т.е. для любых трех отношений и из имеет место равенство .

Произведение двух бинарных отношений для функций можно интерпретировать следующим образом. Пусть и – две функции. Если , , то в результате применения сначала , а потом , каждому элементу ставится в соответствие единственный элемент , т.е. определяется функция . Эту функцию называют произведением функции на функцию (или суперпозицией функций и ) и обозначают через .

Определение 13. Произведением функций и называется функция , для которой

. (10)

Аналогично определяется произведение отображений.

Образно говоря, функция есть результат последовательного применения к аргументу сначала функции , а затем к полученному элементу – функции .

Замечание 3. Обратим внимание на то, что в равенстве (10) порядок записи и в левой и правой части меняется. Этого можно было бы избежать, если бы аргумент писать перед обозначением функции, т.е. в виде

.

Так поступают в некоторой математической литературе, но это является малоупотребительным, так как не согласуется с общепринятой практикой обозначений в школьной и вузовской математике. Иногда произведение на записывают справа налево , но и при этом приходится менять привычную запись произведения.

Пример 10. Пусть , , . На нижеследующем рис. 5 изображены отображения и и их произведение :

: : :

Рис. 5.

Пример 11. Пусть , ; , . Тогда – функция такая, что .

Т е о р е м а 3. Если и – инъективные функции, то их произведение – инъективная функция.

□ Пусть и – любые различные элементы из А. Тогда в силу инъективности и имеем:

.

Таким образом, влечет , что означает инъективность .

Т е о р е м а 4. Если и – сюръективные функции, то их произведение – сюръективная функция.

□ Из сюръективности следует, что , а из сюръективности следует, что . Но тогда , т.е. – сюръективная функция.

Из теорем 3 и 4 вытекает

Следствие 1. Произведение двух биективных отображений биективно.